Znaky intervalového a poměrového typu

U znaků intervalového typu lze stanovit vzdálenost mezi hodnotami měřené veličiny. Je zde definována jednotka měření, avšak nula je definována pouze relativně. To nám dovoluje proto počítat s rozdíly naměřených hodnot, nikoliv s jejich podíly. Typickým příkladem je teplota, která se dá měřit v různých stupnicích (Celsiova, Fahrenheitova).

 

U znaků poměrového typu lze určit nejen rozdíly (intervaly) mezi hodnotami, ale i podíly hodnot, neboť tyto znaky mají nulu stanovenu absolutně a jednoznačně.

 

Definice 3.7. Aritmetický průměr :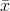

(1)

 

U poměrových znaků, které nabývají pouze kladných hodnot, lze použít geometrický průměr:

(2)

 

(1)	rozptyl:	(3)
(2)	směrodatná odchylka:	(4)
(3)	koeficient variace (pro poměrové znaky):	(5)

Všechny uvedené charakteristiky jsou charakteristikami variability datového souboru.

 

Poznámka 3.9. Rozptyl se zpravidla počítá podle vzorce 

Definice 3.10. Známe-li absolutní či relativní četnosti variant 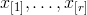,  můžeme spočítat vážený průměr:

(6)

nebo vážený rozptyl:

(7)

Poznámka 3.11. Vážený rozptyl se zpravidla počítá podle vzorce

Aritmetický průměr a rozptyl jsou speciální případy tzv. momentů. V následující definici obecně zavedeme 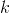-tý počáteční a centrální moment.

k-tý počáteční moment:	(8)
k-tý centrální moment:	(9)

Definice 3.13.

šikmost: Šikmost měří nesouměrnost rozložení četností kolem průměru.	(10)
špičatost: Špičatost měří koncentraci rozložení četností kolem průměru.	(11)

Příklad 3.14. Pro údaje z příkladu Průzkumová analýza jednorozměrných dat 2.3 vypočtěte průměr a rozptyl počtu členů domácnosti.

 

Řešení.

Příklad 3.15. Nechť  je průměr a  rozptyl hodnot . Nechť ,  jsou reálné konstanty. Položme . Vypočtěte průměr  a rozptyl  hodnot .

 

Řešení.