Analýza deviance

Ve výukové jednotce Lineární regresní model jsme se seznámili s analýzou rozptylu a jejím významem pro porovnávání různých lineárních regresních modelů. O tento nástroj u zobecněných lineárních modelů nepřicházíme. Je však potřeba definovat novou statistiku, která bere v úvahu odhad parametrů modelu metodou maximální věrohodnosti. Touto statistikou je tzv. deviance, která je dvojnásobkem rozdílu mezi logaritmem věrohodnosti maximálního modelu (značíme , tedy takový hypotetický model, u kterého modelové parametry a vstupní data splývají, jeho věrohodnost je největší možná) a logaritmem věrohodnosti zkoumaného modelu (značíme ,s omezeným počtem parametrů, jež jsou odhadovány metodou maximální věrohodnosti). 

Uvažujme modelovací příklad s  pozorováními. Výsledky se snažíme modelovat pomocí prediktorů s využitím určitého počtu parametrů. Samozřejmě platí, že čím více parametrů použijeme, tím blíže se s predikcemi dostaneme ke skutečným pozorováním. Zavedeme si tedy následující pojmy:

• Model s parametry
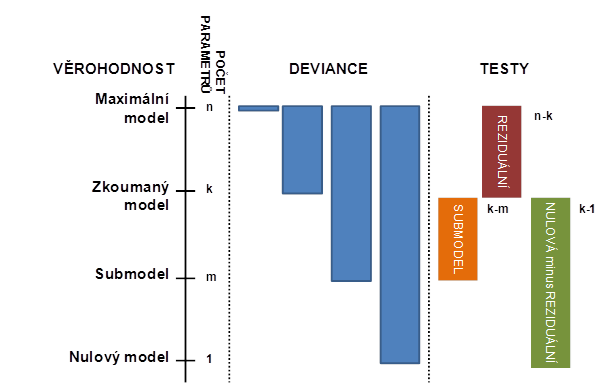
  MAXIMÁLNÍ MODEL veškerá variabilita do systematické složky

• Model s parametry
  ZKOUMANÝ MODEL

• když vyloučíme některý prediktor ( parametrů)
  SUBMODEL

• Model s 1 parametrem (konstantou – průměrem)
  NULOVÝ MODEL veškerá variabilita do náhodné složky

Nyní můžeme podobně jako v analýze rozptylu formálně testovat, zda se od sebe modely ve svých predikčních schopnostech statisticky významně liší. Statistika rozdíl deviancí představuje testové kritérium pro rozdíl mezi zkoumaným modelem a jeho submodelem:

Je-li , kde    představuje kvantil chí-kvadrát rozdělení, je počet odhadovaných parametrů submodelu a k je počet parametrů zkoumaného modelu, pak je submodel nevhodný – přehnaně zjednodušující.

Pro orientační test, zda ve zkoumaném modelu nechybí významný prediktor modelu, můžeme testovat, zda se od sebe liší zkoumaný a maximální model. V tom případě jako testové kritérium použijeme tzv. reziduální devianci a počet stupňů volnosti pro kvantil chí-kvadrát rozdělení je dán rozdílem mezi počtem pozorování (tedy počtem parametrů maximálního modelu) a počtem parametrů zkoumaného modelu.

Pro orientační test, zda náš zkoumaný model vůbec vysvětluje nějakou variabilitu ve srovnání s prostou konstantou, můžeme testovat, zda se od sebe liší zkoumaný a nulový model. V tom případě jako testové kritérium použijeme rozdíl reziduální a nulové deviance (obě tyto statistiky uvádí software R ve standardním výstupu) a počet stupňů volnosti pro kvantil chí-kvadrát rozdělení je dán počtem parametrů zkoumaného modelu zmenšeným o 1. Uvedené vztahy jsou graficky znázorněny na obrázku 3.

Akaikeovo informační kritérium

Pokud se snažíme zvolit nejlepší statistický model vysvětlující daná data, deviance (resp. věrohodnost) nemůže být jediným kritériem. Je jasné, že pokud bychom modely seřadili podle deviance, nejlepší bude právě maximální model, který je ale z praktického hlediska nepoužitelný. Ani vložení všech vysvětlujících proměnných, které máme v našem datovém souboru k dispozici, nemusí být nejlepším řešením – v minulé výukové jednotce jsme zmiňovali problém přeučení modelu. Jako nástroj pro jednoduchý předvýběr zobecněných lineárních modelů se často využívá Akaikeovo informační kritérium (AIC). Součástí tohoto kritéria je vedle logaritmu věrohodnosti () i počet parametrů zkoumaného modelu ().

Čím je hodnota AIC menší, tím považujeme model za lepší. Zahrnutím  (počtu parametrů) AIC penalizuje modely s vysokým počtem použitých parametrů a tak zamezuje přeučení statistického modelu.