Multikolinearita

Síla vícenásobné lineární regrese je v možnosti zjistit samostatný vliv jednotlivých prediktorů na výsledek. V praxi se ale můžeme setkat se situací, kdy to není možné. Problém nastane, když jsou dvě proměnné velmi silně korelovány. Pak není možné příliš dobře určit nezávislý vliv jedné z proměnných na výsledek. Tomuto jevu říkáme multikolinearita.

Vzniklý problém si ukážeme na extrémním příkladu. Představme si, že se snažíme sestavit model pro predikci tělesné výšky (třeba pro účel imputace proměnných, viz další kapitola). Pokud bychom měli v datovém souboru tělesnou hmotnost v kilogramech i librách (1 lb je přibližně 0,45 kg), roztržitému statistikovi by se mohlo stát, že do modelu zahrne obě tyto proměnné. Co by se stalo?

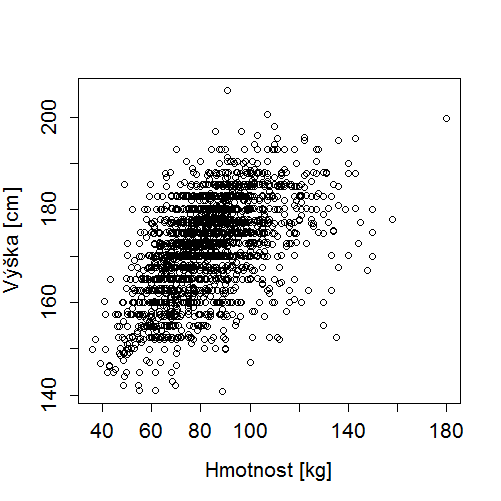
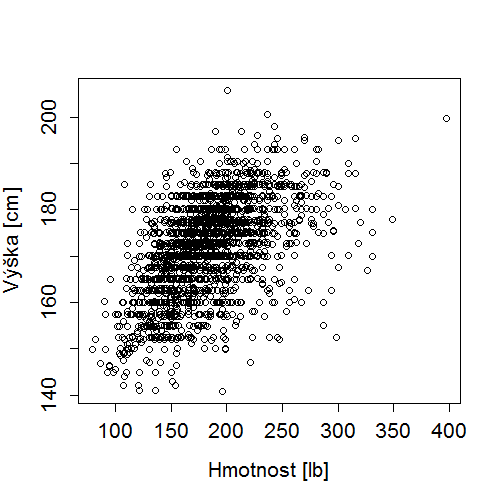
Ukážeme si nejprve, jak by regresní přímky vypadaly pro dva modely závislosti tělesné výšky na hmotnosti, nejprve v kg a poté v librách. Použijeme data účastníků epidemiologické studie GUSTO-I [gusto].

Výška = 147 + HmotnostKg x 0,3	Výška = 147 + HmotnostLb x 0,14

Data v obou x-y grafech vypadají naprosto stejně (až na měřítko osy x). Podobná bude tedy samozřejmě i regresní rovnice (až na sklon přímky, který se liší právě násobením převodní konstantou). Spočítejme, jak by mohly vypadat odhady regresních koeficientů:

model s oběma prediktory	Výška = + HmotnostKg ∙ + HmotnostLb ∙
1. možnost: model s kilogramy	Výška = 147 + HmotnostKg ∙ 0,3 + HmotnostLb ∙ 0
2. možnost: model s librami	Výška = 147 + HmotnostKg ∙ 0 + HmotnostLb ∙ 0,14
změníme jednotku	Výška = +(HmotnostLb ∙ 0,45)∙ + HmotnostLb ∙
a použijeme původní odhad	Výška = + HmotnostLb ∙ ( 0,45 ∙ +

Z toho však plyne, že optimální model je kterýkoliv, pro jehož koeficienty a platí .

A takových je nekonečně mnoho, odhad parametrů lineárního modelu tedy samozřejmě selže.

V praxi, pokud neuděláme podobnou chybu, proměnné takto dokonale korelované nejsou. Setkáme se však s proměnnými, jejichž korelace je vysoká. V takovém případě nemusí být možné správně určit příspěvek jednotlivých proměnných k celkovému efektu a model tedy selže ve své základní funkci.

Abychom se těmto problémům vyhnuli, musíme si riziko multikolinearity uvědomovat a umět tento jev v našem datovém souboru poznat. Nejjednodušším nástrojem je určení matice korelačních koeficientů. Z ní můžeme zjistit, které proměnné spolu vysoce korelují (korelační koeficient v absolutní hodnotě blízký 1). Užitečná může být rovněž matice korelačních koeficientů mezi odhady regresních koeficientů. Ta se běžně ve výsledcích neuvádí, programy pro regresní analýzu ji však umí zobrazit.

Tento jednoduchý postup má jeden zásadní problém: multikolinearita nemusí znamenat korelaci jen mezi dvěma proměnnými, ale rovněž situaci, kdy se dá jedna z proměnných odvodit jako lineární kombinace několika jiných proměnných).

Řešením je použít místo korelačního koeficientu tzv. variance inflation factor (faktor zvětšení rozptylu, VIF). Tento ukazatel měří, nakolik je rozptyl odhadovaných regresních koeficientů zvětšen ve srovnání se situací, kdy by prediktory byly vzájemně nezávislé [1].

je koeficient mnohonásobné korelace (odmocnina koeficientu determinace regresního modelu pro závislost tohoto prediktoru na ostatních prediktorech). Jako orientační pravidlo lze říci, že hodnoty VIF > 4 mohou být problematické, hodnoty > 10 mohou závažně ovlivnit výsledky modelování [2].

V modelu bychom samozřejmě závažně korelované prediktory neměli nechávat. Vyloučit lze z analýzy nejlépe proměnné obsahující chybějící data, proměnné obecně hůře měřitelné, nebo z jiných důvodů méně důvěryhodné. Řešením může být také vytvoření „a/nebo“ proměnné z korelovaných kategoriálních proměnných, případně kombinace prediktorů do jediného skóre (typickým případem je vytvoření indexu tělesné hmotnosti z korelovaných proměnných výška a tělesná hmotnost).