Definice logistického regresního modelu
Cílem logistického regresního modelu je modelování náhodného výběru proměnných s binárním výsledkem. Rozdělení takového výsledku je možné popsat binomickým rozdělením. Binomické rozdělení je diskrétní rozdělení, které popisuje počet výskytů sledované události (ve formě nastala/nenastala) v sérii nezávislých experimentů, kdy v každém experimentu je stejná pravděpodobnost výskytu události
.
Binomické rozdělení má následující pravděpodobnostní funkci:
Známe-li parametr , pak podle počtu experimentů známe střední hodnotu a rozptyl
Abychom logistický regresní model nadefinovali, uvažujme jeden z nezávislých experimentů (jedno pozorování). Výsledek tohoto experimentu je rozdělený alternativně (nabývající hodnoty 1 s pravděpodobností , jinak nabývá hodnoty 0):
Srovnejme lineární regresi (vlevo) s logistickou regresí (vpravo)
|
modelujeme spojitý výsledek
hodnota parametru (střední hodnoty) je rovna lineárnímu prediktoru
|
modelujeme nastání náhodného jevu
hodnota parametru (střední hodnoty) je rovna transformovanému prediktoru
hodnota lineárního prediktoru odpovídá střední hodnotě transformované linkovací funkcí logit
|
Proč ale vůbec tuto linkovací funkci používáme?
Pokud bychom linkovací funkci nepoužili (tedy použili jako linkovací funkci identitu, tak jako v lineární regresi), pak bychom jako hodnotu pravděpodobnosti dostávali různá reálná čísla. Nepochybně ale nechceme jako modelovanou pravděpodobnost čísla menší než 0 nebo větší než 1.
Uvažujme tedy zmíněnou funkci logit:
a její inverzi (někteří autoři ji označují jako „expit“):
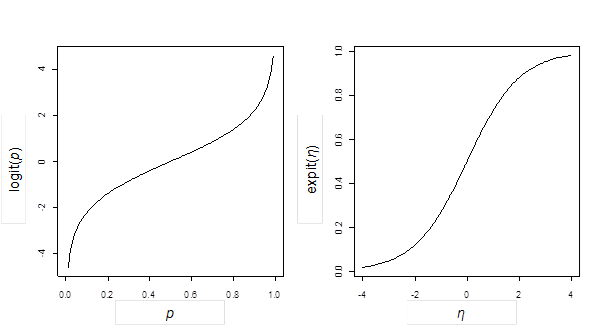
Za komplikovanými vztahy se skrývají velmi užitečné vlastnosti této funkce. Ukažme si je na následujících grafech (obr. 1). Podíváme-li se na pravý obrázek, vidíme, že zatímco lineární prediktor může nabývat libovolných hodnot na reálné ose, transformace expit nám zajistí, že výsledek bude v oboru hodnot od nuly do jedné (asymptoty jsou opravdu v 0 a 1).
Obr. 1: Linkovací funkce a její inverze (expit) v logistickém regresním modelu