Relativní přežití v čase , , odhadujeme dle (6.1) jako poměr celkového přežití a očekávaného přežití . Celkové přežití v populačním hodnocení nejčastěji odhadujeme pomocí metody úmrtnostních tabulek (viz kapitola 3), která na rozdíl od Kaplanovy-Meierovy metody pracuje s časovými intervaly. Pro připomenutí uveďme odhad celkového přežití do konce -tého intervalu pomocí metody úmrtnostních tabulek, který je dán vztahem

$\hat{S} (J) = \overset{J}{\prod_{j = 1}} {\hat{p}}_{j} = \overset{J}{\prod_{j = 1}} (1 - \frac{d_{j}}{R_{j} - \frac{c_{j}}{2}})$

(6.2)

kde je počet úmrtí, počet cenzorovaných časů přežití a počet pacientů v riziku v -tém časovém intervalu.

Výpočet očekávaného přežití do konce -tého intervalu, , je založen na mortalitních tabulkách s ročními intervaly. Odhad pro skupinu pacientů zahrnuje výpočet očekávané pravděpodobnosti přežití pro každého pacienta podle celkové populace s ohledem na věk, pohlaví a období (např. datum stanovení diagnózy). V současnosti jsou využívány čtyři metody vhodné pro odhad očekávaného přežití v populačním hodnocení přežití: metoda dle Ederera I, metoda dle Ederera II, Hakulinenova metoda a metoda dle Pohar-Perme:

Metoda dle Ederera I je nejjednodušší metodou k odhadu očekávaného přežití odpovídajícího hodnocené skupině pacientů. Jeho hodnota je stanovena jako průměrné očekávané přežití jedinců z obecné populace (odpovídající -tému pacientovi věkem, pohlavím a obdobím) bez ohledu na stav příslušného -tého pacienta, tedy vztahem

$S * (J) = \overset{n}{\sum_{i = 1}} \frac{S_{i} * (J)}{n} = \overset{n}{\sum_{i = 1}} \frac{\prod_{j = 1}^{J} s_{i j} *}{n}$

(6.3)

kde je celkový počet pacientů v riziku na začátku sledování (v čase 0) a je očekávaná pravděpodobnost přežití do času (standardně do konce -tého intervalu) pro -tého jedince z obecné populace. Hodnota pak představuje intervalově specifické očekávané přežití -tého jedince z obecné populace pro -tý interval. Konkrétní hodnota přežití (kompletní či cenzorovaná) tak nemá na celkové očekávané přežití žádný vliv. Tato metoda poskytuje nezkreslený odhad očekávaného přežití, není však příliš vhodná pro výpočet relativního přežití, neboť současně s odhadem celkového přežití, které je zkresleno cenzorováním, může poskytovat stejně zkreslený odhad relativního přežití.

Metoda dle Ederera II byla navržena tak, aby bylo možné zohlednit různě dlouhé sledování různých jedinců (pacientů). Odhad očekávaného přežití je opět kalkulován jako průměrné očekávané přežití jedinců z obecné populace, tentokrát však se zohledněním pozorovaných hodnot (kompletních i cenzorovaných) příslušného -tého pacienta, tedy pomocí vztahu

$S * (J) = \overset{J}{\prod_{j = 1}} S_{j} * = \overset{J}{\prod_{j = 1}} \overset{R_{j}}{\sum_{i = 1}} \frac{s_{i j} *}{R_{j}}$

(6.4)

kde je průměrná očekávaná pravděpodobnost přežití pro -tý interval, kterou opět kalkulujeme z intervalově specifických hodnot očekávaného přežití , ale jen u pacientů, kteří jsou v riziku (naživu) na začátku -tého časového intervalu (skupina pacientů v riziku ).

Hakulinenova metoda [1] byla dlouho považována za nejvhodnější metodu pro výpočet očekávaného přežití a následné relativní přežití, neboť se snaží vypořádat se zkreslením, které do odhadu přežití vnáší cenzorování. Myšlenka Hakulinenovy metody spočívá ve výpočtu zkresleného odhadu očekávaného přežití se zkreslením odpovídajícím zkreslení odhadu pozorovaného přežití s cílem, aby následný poměr zkresleného pozorovaného a očekávaného přežití vytvořil celkově nezkreslený odhad relativního přežití.
Metoda dle Pohar-Perme [2] je relativně nová metoda odhadu relativního přežití, která však nepracuje s očekávaným přežitím jako předchozí metody. Naopak kalkuluje z populačních úmrtnostních tabulek tzv. riziko spojené s daným onemocněním (excess risk), které následně přepočítává na relativní přežití. Tato metoda je některými autory doporučována, na místě je však třeba dodat, že všechny zde uvedené způsoby výpočtu očekávané a potažmo relativního přežití dávají v krátkodobém časovém horizontu (1 leté až 5leté relativní přežití) velmi podobné výsledky a začínají se lišit až při odhadech dlouhodobého přežití (10 leté a víceleté přežití).

Máme-li k dispozici odhady pozorovaného i očekávaného přežití, lze relativní přežití do konce -tého intervalu jednoduše spočítat dosazením do vztahu (6.1). Obě komponenty poměru, čitatel i jmenovatel, lze v případě použití metody dle Ederera II nebo Hakulinena dále specifikovat jako součin intervalově specifických pravděpodobností pro všech intervalů, a to následujícím způsobem

$R (J) = \frac{S (t)}{S * (t)} = \frac{\prod_{j = 1}^{J} {\hat{p}}_{j}}{\prod_{j = 1}^{J} S_{j} *} = \overset{J}{\prod_{j = 1}} r_{j}$

(6.5)

Hodnoty nazýváme intervalově specifický odhad relativního přežití (interval specific relative survival) pro -tý interval a jsou stejně důležitou komponentou hodnocení populačního přežití jako kumulativní hodnoty. Hodnoty intervalově specifického relativního přežití totiž souvisí s pojmem statistické vyléčení (statistical cure). Místo kumulativního odhadu relativního přežití lze do grafu vynést i odhady pro jednotlivé intervaly a ve chvíli, kdy odhad intervalově specifického relativního přežití dosáhne hodnoty 1, lze říci, že se mortalita sledovaných pacientů v daném intervalu dostala na úroveň mortality populační. Jako příklad lze uvést diagnózy zhoubný novotvar (ZN) žaludku a ZN prsu. V případě ZN žaludku se intervalově specifické relativní přežití po 8 až 10 letech dostává na úroveň hodnoty 1, což znamená, že cca po 10 letech můžeme pacienta se ZN žaludku považovat v podstatě za vyléčeného. Na druhou stranu, v případě ZN prsu je intervalově specifické relativní přežití i po 10 letech pod hodnotou 1, což znamená, že ZN prsu je diagnóza, která se pacientkám opakovaně vrací a tudíž vykazuje známky chronického dlouhodobého onemocnění [3]. Je však třeba poznamenat, že nelze zaměňovat pojmy klinické a statistické vyléčení. Pojem klinické vyléčení totiž chápeme na úrovní jedince jako vymizení všech klinických projevů nemoci, zatímco pojem statistické vyléčení chápeme na úrovni skupiny pacientů jako srovnání mortality s populační úrovní.

I přes zřejmé výhody výpočtu relativního přežití je vždy přínosné ho doplnit také výpočtem pozorovaného přežití. Nepřímo nám tyto dvě hodnoty, relativní a pozorované přežití, dávají informaci o věkové struktuře pacientů s danou diagnózou. Příklad tohoto srovnání je uveden na obrázku 6.1, z něhož je vidět, že u diagnózy s výrazně mladší věkovou strukturou jako je např. ZN varlete jsou tyto odhady téměř totožné, zatímco u diagnózy s výrazně starší věkovou strukturou, jako je např. ZN prostaty, mohou být tyto hodnoty hodně odlišné. U karcinomu prostaty toto srovnání také naznačuje, že samotný nádor ve stadiu I nebo II nepředstavuje pro tyto pacienty výrazné riziko a tito pacienti tak umírají zejména v souvislosti s pokročilým věkem na jiná onemocnění. Výpočet relativního přežití může dokonce u některých méně závažných diagnóz zachycených v časném stadiu vést k hodnotám nad 1 (nad 100 %), což může být např. důsledkem zvýšené lékařské péče nebo zdravějšího života onkologických pacientů po stanovení diagnózy. V tomto případě má svůj význam opět i 5leté pozorované přežití, které nám dává informaci o celkové úmrtnosti těchto pacientů.

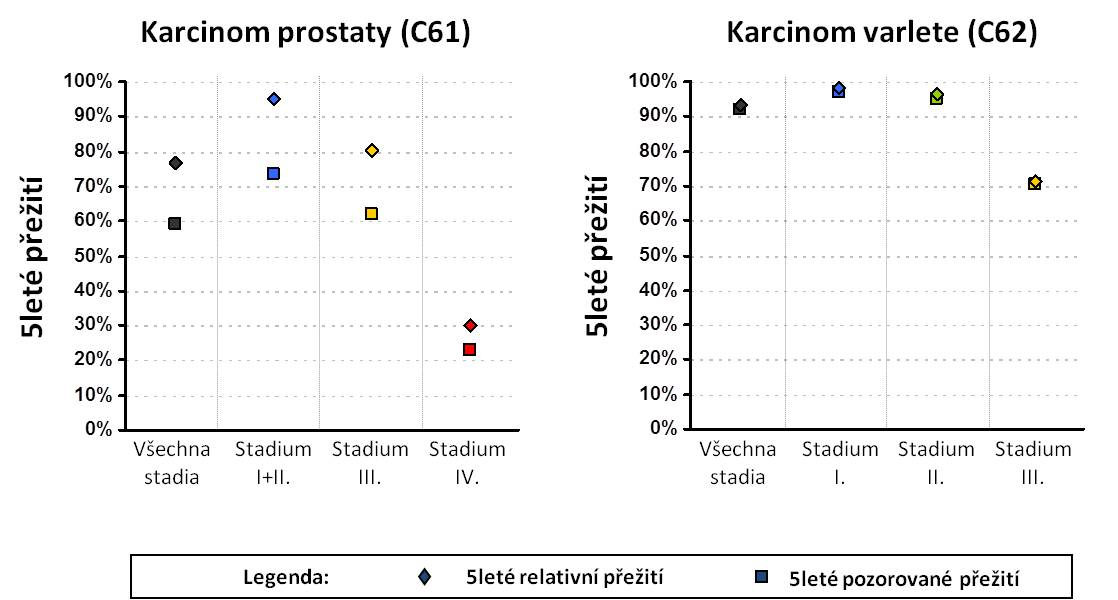Obr: 6.1 Srovnání hodnot 5letého pozorovaného a relativního přežití pacientů léčených protinádorovou terapií u vybraných diagnóz (analýza periody 2003-2005).

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity