Konsenzusové shlukování

Konsenzusové shlukování je metoda shlukové analýzy, která je založena na opakovaném převzorkování a shlukování datového souboru, s cílem změřit konsenzus výsledků (Monti a kol., 2003). Míra konsenzusu se dá použít pro:

• odhad počtu a stability objevených shluků
• jako míra citlivosti algoritmu na změnu dat

Konsenzusové shlukování navíc slouží jako vizualizační nástroj, pomoci kterého je možné vyhodnotit počet a stabilitu shluků i vzorků (např. jak často se daný vzorek vyskytuje ve shluku s jiným vzorkem?).

Základní princip je rozrušení struktury originální datové matice N × P a to náhodým výběrem podmnožiny vzorků nebo proměnných (genů, proteinů). Na nový datový soubor je pak aplikován shlukovací algoritmus a vzorky rozděleny do předem vybraného počtu shluků. Toto převzorkování se opakuje L krát. V každém l-tém běhu jsou zaznamenány údaje o příslušnosti vzorků ke shluku a to pomocí dvou matic o dimenzi N × N:

• Matice konektivity C^(l), která ukládá pro každý pár vzorků i,j informaci, jestli byli ve společném shluku, tedy: C^(l)_ij=1, když vzorek i a j byly ve společném shluku a 0 v opačném případě
• Indikátorová matice I^(l) , která ukládá pro každý pár vzorků i,j informaci, jestli byly společném výběru, tedy: I^(l)_ij=1, když vzorek i a j byly ve společném výběru a 0 v opačném případě

Po všech l běhech je vypočtená matice konsenzusu M, jako podíl počtu kolikrát byly dva vzorky ve společném shluku k počtu kolikrát tyto vzorky byly ve společném výběru. Matice konsenzusu má tedy také dimenzi N × N a pro každý pár vzorků ukládá vážený podíl počtu běhů, ve kterých dva vzorky byly společně ve shluku:

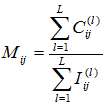
Základní myšlenka celého tohoto přístupu je že vzorky, které jsou často nalezeny ve společném shluku představují důvěryhodnější členy shluku než ty, které se spolu vyskytují méně často v důsledku své citlivosti na náhodné změny počtu vzorků nebo proměnných.

Každé pole matice konsenzusu představuje index konsenzusu páru vzorků, který nabývá hodnoty od 0 (žádný konsenzus, vzorky se nikdy nevyskytli v jednom shluku) do 1 (perfektní konsenzus, vzorky byly ve společném shluku ve 100 % běhů). Matice konsenzusu M tak reprezentuje robustní míru podobnosti, ze které lze jednoduše odvodit míru vzdálenosti jako 1-M. Tato míra vzdálenosti pak může být použita pro finální robustní shlukování všech vzorků.

Obrázek X níže zobrazuje výsledek hierarchického shlukování s použitím míry vzdálenosti odovzené od matice konsenzusu na souboru bez struktury (náhodný výběr z normálního rozložení, A.) a příkladová data golub se strukturou tří skupin (B):

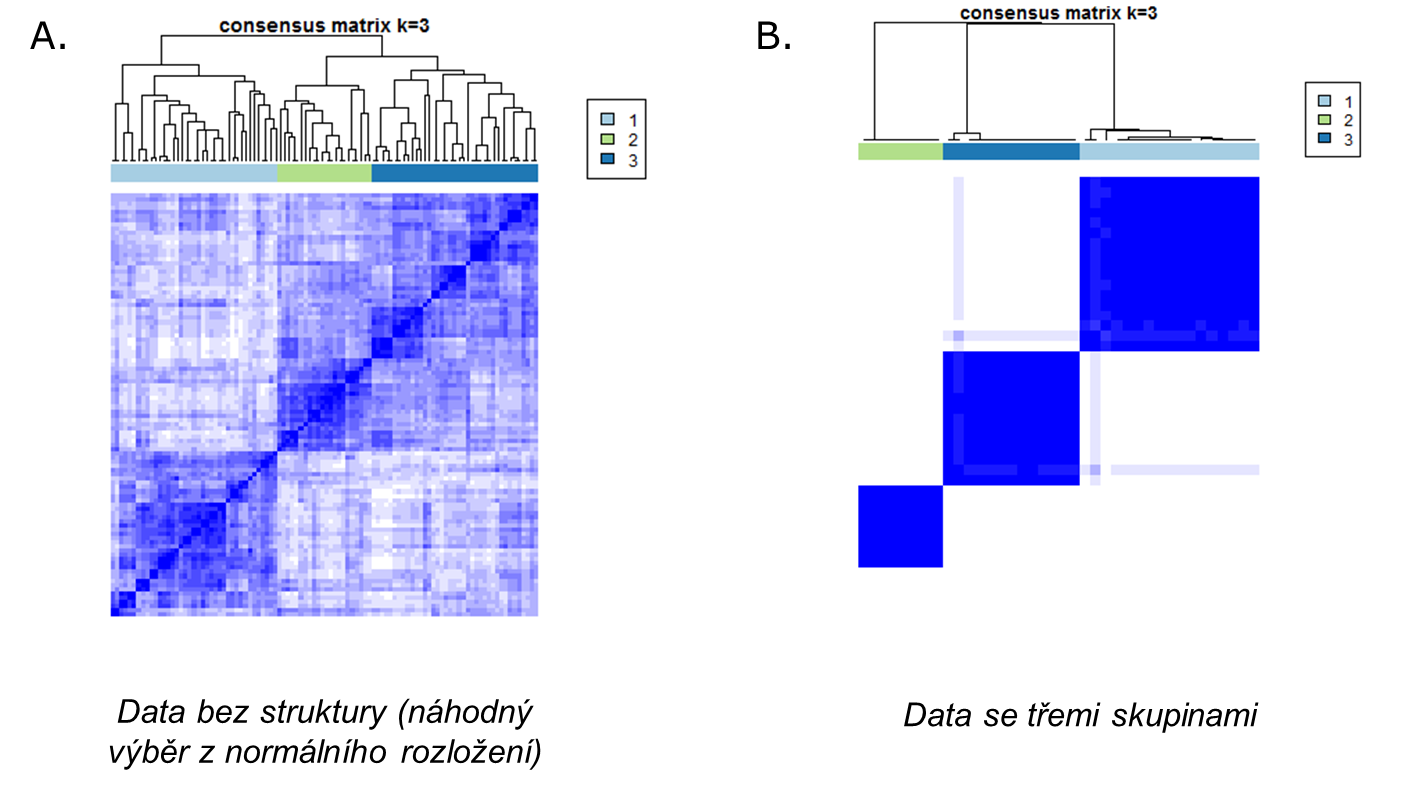
Obrázek X. Výsledek hierarchického shlukování na matici konsenzusu na příkladových datech. Bílá znamená nulový konsenzus, modrá konsenzus 1. A. výsledek na datech bez struktury, B. výsledek na příkladovém souboru golub, představující tři typy akutní leukemie. 

Vidíme, že zatímco v prvním případě nedokážeme rozpoznat na obrázku strukturu skupin, v datovém souboru golub již vidíme tři skupiny se silným konsenzusem uvnitř a nulovým konsenzusem mezi skupinami.

Matici konsenzusu mezi vzorky je možno přímo použít k definování statistiky stability samotných shluků a také stability přiřazení vzorků ke shlukům. Pokud je I_k soubor indexů vzorků které patří ke skupině k, míra konsenzusu shluku k - konsenzus shluku- může být definována jako průměrný index konsenzusu mezi všemi páry vzorků, které patří do stejného shluku:

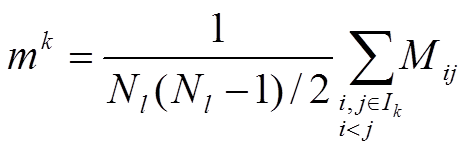
Odpovídající konsenzus vzorku v shluku  pro každý vzorek s_i a shluk l se definuje jako:

,

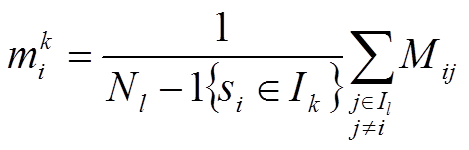kde je indikátorová funkce, která je rovna 1 pokud platí  a 0 jinak. Konsensus vzorku je tedy průměrný index všech indexů konsenzusu vzorku ke všem ostatním vzorkům daného shluku.

Obe míry se mohou použít k identifikaci odlehlých hodnot, což jsou buď shluky s nízkou mírou konsenzusu, což vypovídá o heterogenitě uvnitř shluku, nebo jsou to vzorky, které mají velice malý konsenzus s jakýmkoliv jiným vzorkem datového souboru.

Odhad optimálního počtu shluků

Matice konsenzusu může být použita i pro odhad optimálního počtu shluků. Konsenzusové shlukování můžeme provést pro různé počty shluků k=1..K, a rozhodovací pravidlo o počtu shluků pak můžeme například založit na výpočtě průměrného konsenzusu v každém shluku pro každé k. Monti a kol. navrhují jinou míru - empirickou kumulativní distribuční funkci (CDF):

,

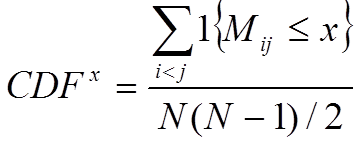která porovnává rozložení histogramů prvků matice konsenzusu M pro každé k. Pokud shlukování s k shluky reprezentuje perfektní rozdělení, histogram konsenzusů mezi vzorky bude mít pouze dva sloupce: jeden na hodnotě 0 (žádný konsenzus mezi vzorky s různých shluků) a jeden na hodnotě 1 (perfektní konsenzus mezi vzorky ze stejného shluku). Optimální počet shluků je pak rozhodnut vypočtením ploch pod CDF křivkami jednotlivých počtů shluků a porovnáním relativní změny mezi různými shlukováními (plocha delta). Metrika CDF je však použitelná zejména pokud algoritmus použitý v konsenzusovém shlukování je hierarchické shlukování, což je metoda, pro kterou byla CDF navržena. Obrázek Y níže na našich příkladových datech golub ukazuje histogram pro výsledky konsenzusového shlukování pro k=3 a k=6 shluků,  CDF křivky pro 2 až 10 shluků a graf delta ploch.

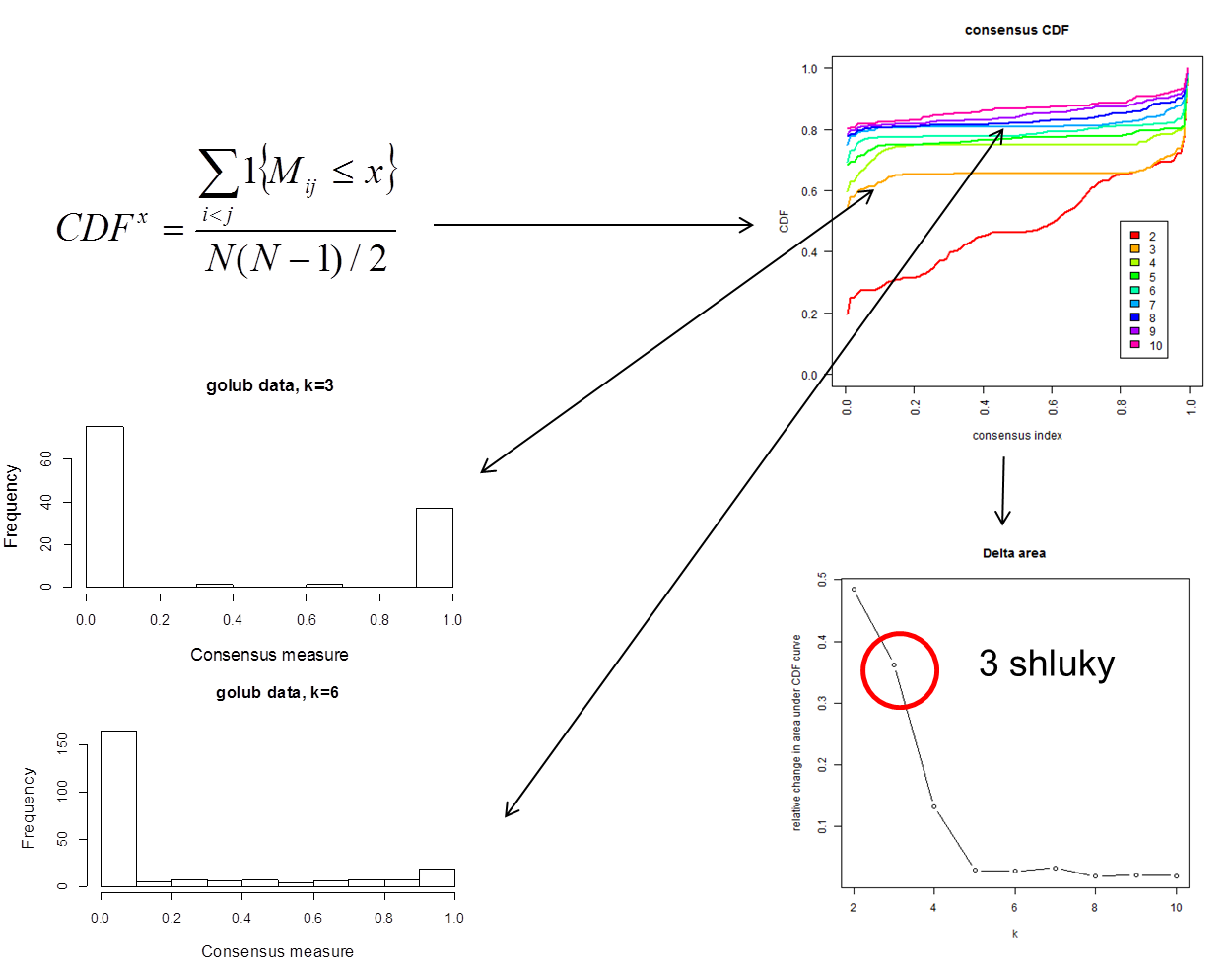
Obrázek Y. Příklad výpočtu CDF a výběr počtu shluků u příkladového souboru golub.

Jak vidíte, histogram konsenzusu mezi vzorky pro shlukování o k=3 ukazuje, že většina hodnot je opravdu 0 nebo 1. Histogram pro shlukování o k=3 naopak ukazuje podstatné snížení konsenzusových hodnot 0 a 1 a zvýšení hodnot mezi 0 a 1. Graf delta ploch ukazuje, že zvýšení počtu shluků ze 2 na 3 se plocha pod křivkou zvětší o 0.36. Další zvětšování počtu shluků přináší pouze malé změny v celkové ploše pod CDF křivkou (0.14 pro k=4 a méně než 0.05 pro k>4). Kromě delta plochy je také nutno všímat si tvar CDF křivky. V ideálním případě prudce stoupá v nízkých hodnotách (mezi 0 a 0.1), pak je konstatní a pak znovu prudce stoupá kolem 0.9-1. To proto, že se jedná o kumulativní funkci, tedy mezi 0.1 a 0.9 by se v případě perfektního rozdělení do shluků neměla u těchto hodnot zvyšovat.

Na základě těchto informací vybereme k=3 jako odhad počtu shluků.

Další metody konsenzusového shlukování

Existuje několik variací konsenzusového shlukování, které jsou vlastně jakýmsi rozšířením původního algoritmu.

Metoda zvaná spojené konsenzusové shlukování (Swift a kol., 2004), definuje matici konsenzusu jako funkci výsledků konsenzusového shlukování za použití různých algoritmů (tedy ne pouze hierarchického shlukování, jako u původní metody. To by mělo eliminovat případný nepříznivý vliv jediného algoritmu, který nemusí být vhodný pro daný typ dat.

Vážené konsenzusové shlukování (Deohdar a Ghosh, 2006) zas staví na myšlence, že shluky vytvořené v rámci konsenzusového shlukování nejsou nutně stejné kvality. Existuje-li nějaká externí míra kvality shluků, měli bychom ji schopni integrovat jako váhu příspěvků jednotlivých shluků do konečné matice konsenzu, která se tedy definuje jako

,

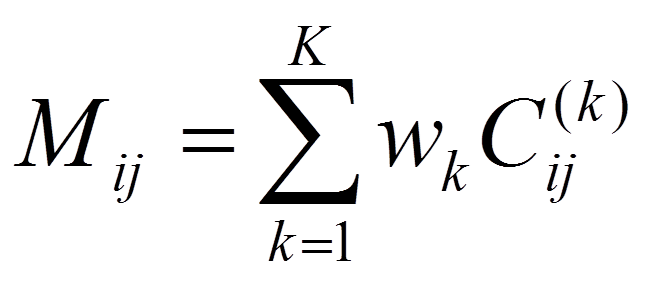kde w_k je váha k-tého shluku. Tato metoda také používá různé shlukovací algoritmy a také různé míry vzdálenosti. Otázkou však zůstává, jsou-li výsledky přístupů míchajících různé algoritmy shlukování a/nebo metriky vzdáleností opravdu relevantní - každý algoritmus a metrika má jiný pohled na data a jejich promíchání může naopak výsledky znepřehlednit.

Pro porovnání různých shlukovacích algoritmů doporučujeme práci (Goder a Filkov, 2008).

R-balíky ke konsenzusovému shlukování

V R existují dva hlavní balíky pro konsenzusovou analýzu. Balík ConsensusClusterPlus a poskytuje všechny algoritmy a metriky i grafy tak jako jsou definovány v textu výše (podle práce Monti a kol, 2013). Balík je součástí nástavby R - Bioconductor a nainstalujete ho přímo z R konzoly zadáním těchto příkazů:

> source(“http://bioconductor.org/biocLite.R”)

> biocLite(“ConsensusClusterPlus”)

Další balík clusterCons implementuje spojené konsenzusové shlukování (Swift et al., 2004). Tento balík se dá nainstalovat přímo z R konzoly zadáním příkazu:

> install.packages("clusterCons")