Kinetika chemických reakcí

Pro kinetický popis biochemických reakcí se jako vhodné (nezbytné) ukázalo matematické modelování. Obzvláště zajímavá je kinetika enzymových reakcí, jejímž principům se v této kapitole budeme věnovat. Vycházíme přitom především z monografií [1] (kapitola 1), [2] (kapitola 11) a [3]. Více formálně matematický pohled na uvedenou problematiku čtenář nalezne také v příslušné kapitole textu Spojité deterministické modely.

Nejdříve si vysvětlíme užívaná schématická značení a způsob sestavování rovnic matematického modelu. Uvažujeme chemickou reakci, v níž molekula látky A reaguje s molekulou látky B za vzniku molekuly látky C. Naopak, molekula C se za určitých podmínek může rozpadnout na molekuly složek A a B. Pro popis množství látek v čase se používá veličina koncentrace. Tu lze uvažovat v několika variantách, např. jako hmotnost látky v jednotkovém objemu, jako molární množství látky v jednotkovém objemu, anebo jako počet molekul látky v jednotkovém objemu. Standardně užívanou koncentrací pro popis biochemických reakcí je molární množství látky v jednotkovém objemu. Ačkoliv odpovídající jednotkou v soustavě SI je mol m^-3, v praxi obvykle používanou jednotkou je mol dm^-3, někdy zkráceně označovanou symbolem M. Pro matematický popis dynamiky reakce zavedeme nezáporné funkce označující koncentraci látek A, B, C v čase

Tradičně se předpokládá, že rychlost tvorby látky C je úměrná koncentracím látek A i B, tento princip je nazýván law of mass action. Tento předpoklad znamená, že pokud koncentrace látky B vzroste na dvojnásobek (resp. trojnásobek), rychlost tvorby látky C bude také dvojnásobná (resp. trojnásobná). Pokud koncentrace látky B vzroste dvakrát a koncentrace látky A třikrát, rychlost tvorby látky C vzroste dokonce šestkrát. Takový předpoklad bude splněn při nízkých koncentracích, kdy se každá molekula pohybuje nezávisle na ostatních molekulách. V této situaci znamená zvýšení koncentrace látky B úměrný nárůst počtu „srážek“ molekul látek A a B, které mohou vést ke vzniku látky C a tedy odpovídajícímu nárůstu koncentrace látky C.

Dále předpokládáme, že molekuly C se chovají vzájemně nezávisle, tedy že molekula C se určitou danou a pro všechny molekuly C stejnou pravděpodobností za jednotkový čas rozpadne na molekuly A a B.

Při obou předpokladech o tvorbě a rozpadu látky C zavedeme konstanty úměrnosti udávající podíl A-B-kolizí vedoucích ke vzniku C za jednotku času,
a udávající průměrný počet rozpadů molekul C za jednotku času. Tyto konstanty úměrnosti jsou nazývány rychlostními konstantami (rate constants) a jejich podíl je někdy označován jako tzv. disociační konstanta

(1)

Rychlostní konstanty přitom nemají stejné jednotky. Typicky, jednotkou rychlostních konstant popisujících analýzu je převrácená hodnota jednotky času, zatímco jednotkou rychlostních konstant spojených se syntézou je převrácená hodnota součinu jednotky času a koncentrace. Disociační konstanta proto není bezrozměrnou veličinou, ale má rozměr koncentrace.

Uvažovaná reakce se graficky znázorňuje pomocí tzv. kinetického schématu

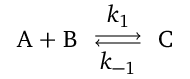(2)

kde znak naznačuje slučování (syntézu), resp. rozklad (analýzu), látek a dvojitá šipka označuje reverzibilní reakci. Ireverzibilní reakce se označují jen šipkou jednoduchou. Veličina uvedená u každé šipky je pak rychlostní konstantou pro příslušnou reakci, příp. zvlášť pro každý směr reverzibilní reakce.

Pro popis dynamiky systému potřebujeme matematické vyjádření změn koncentrací v závislosti na časové změně. Koncentrace proto často považujeme za spojité a diferencovatelné funkce času a dynamiku reakce matematicky vyjadřujeme pomocí (systému) diferenciálních rovnic. Z interpretačních důvodů může být názornější začít sestavením diferenčních rovnic, z nichž pak limitním přechodem obdržíme rovnice diferenciální. Tento postup pro názornost použijeme i my při sestavování první rovnice.

Sledujeme schéma Enzymová kinetika (2) a popíšeme změnu koncentrace, látky C za krátký časový interval délky Během uvažované krátké doby koncentrace látky C naroste o sloučením látek A a B. Využíváme zde law of mass action, konstanta udává, kolik nových molekul se vytvoří při jednotkových koncentracích látek A a B za dobu jednotkové délky, za interval délky se tedy sloučí molekul. Reakce je však reverzibilní, současně dochází k rozpadu látky C, tedy ke snižování koncentrace Součin udává počet rozpadů za interval délky při jednotkové koncentraci látky C. Současným použitím obou směrů reakce sestavíme diferenční rovnici

(3)

Tuto rovnici vydělíme výrazem a limitním přechodem dospějeme k derivaci

(4)

čímž Enzymová kinetika (4) přejde v diferenciální rovnici pro koncentraci látky C,

(5)

Tuto rovnici využijeme pro určení jednotek konstant a Pokud koncentrace látek A, B, C uvažujeme v jednotkách mol dm^-3, je rozměr levé strany Enzymová kinetika (5) mol dm^-3s^-1. Aby to zůstalo zachováno i pro pravou stranu této rovnice, musí být jednotka konstanty rovna převrácené hodnotě jednotky času, tedy s^-1, a rozměr konstanty musí být rovný převrácené hodnotě koncentrace za čas, tzn. mol^-1dm³s^-1.

Analogicky se sestaví diferenciální rovnice pro koncentrace látek A a B, detailní postup přenecháváme čtenáři,

(6)

(7)

Specifikací počátečních koncentrací jednotlivých látek,

(8)

je pak počáteční úloha Enzymová kinetika (5)-(8) jednoznačně zadána a lze analyticky nebo numericky hledat její řešení. Cílem toho textu však není obecné řešení uvedené úlohy, ale její aplikace na konkrétní enzymovou reakci, kterou probereme v následující části. Na závěr této obecné části si ještě všimněme, že sečtením Enzymová kinetika (5) a Enzymová kinetika (6), obdržíme

(9)

což znamená, že součet je konstantní v čase. Podobně, sečtením Enzymová kinetika (5) a Enzymová kinetika (7), resp. Enzymová kinetika (6) a Enzymová kinetika (7), obdržíme další dvě rovnice. Spolu s počátečními podmínkami Enzymová kinetika (8) to znamená, že platí vztahy

(10)

vyjadřující zákon zachování hmoty látek reagujících v uzavřené soustavě.

Poznámka 1.1. (law of mass action a incidence).

V biochemických reakcích standardně užívaný princip law of mass action má blízko pojmu incidence, používanému např. při modelování šíření infekčních chorob nebo v analýze přežití. Vysvětlení souvislosti těchto pojmů proto věnujeme tuto poznámku.

Jako tzv. contact rate se označuje průměrný počet kontaktů objektu (např. látky A, osoby infikované chorobou) za jednotku času. Konstanta zde označuje celkový počet zkoumaných objektů (molekul látky, osob), které jsou rozděleny do dvou kategorií, A a B. Incidencí označujeme průměrný počet nově zformovaných objektů (např. látky C, počet přenosů infekce) všemi objekty za jednotku času. Přitom incidence, se počítá jako součin contact rate počtu objektů kategorie A a pravděpodobnosti že kontakt je uskutečněn s objektem jiné kategorie (např. s látkou B, s osobou náchylnou k infekci),

(11)

V matematických modelech se používají dva typy incidencí:

1. standardní incidence (standard incidence, frequency-dependent incidence) odpovídá případu, kdy je konstantní, nezávislá na celkovém počtu objektů Pro incidenci dostáváme

(12)

2. mass-action incidence (density-dependent incidence), modelující případ, kdy je závislá (lineárně) na celkovém počtu objektů Odpovídající incidence je rovna

(13)