Mikroskopický pohled a náhodná procházka

Difuzí rozumíme proces náhodného přesunování molekul nebo malých částic vyplývající z pohybu na základě tepelné energie, přičemž trajektorie pohybu jednotlivých částic lze považovat za náhodné. Jako typické příklady difuze uveďme pohyb molekul nebo jednoduchých organismů, např. bakterií. Částice s absolutní teplotou (jednotkou je kelvin, K), má v průměru kinetickou (pohybovou) energii (jednotkou SI je joule, J)

(1)

podél každé z os v prostoru. Přitom je tzv. Boltzmannova konstanta. Albert Einstein v jednom se svých nejslavnějších článků z roku 1905 dokázal, že tento vztah platí bez ohledu na velikost částice, dokonce i pro ty, které jsou pozorovatelné mikroskopem a vykazují Brownův pohyb. Částice o hmotnosti a rychlosti podél -ové osy má okamžitou kinetickou energii

(2)

Tato sice kolísá, ale v průměru (značíme čarou nad veličinou) musí platit

(3)

odkud můžeme vyjádřit střední kvadratickou rychlost částice,

(4)

Rovnici Difuze (4) lze použít pro odhad rychlosti malé částice, například molekuly lysozymu. Lysozym je enzym, který se vyskytuje např. ve slinách, slzách, vaječném bílku, nosním hlenu, krevní plazmě a mateřském mléce, a má silné antibakteriální účinky. Hmotnost 1 molu lysozymu, je Jeden mol má přitom molekul, toto množství je dáno tzv. Avogadrovou konstantou. Hmotnost jedné molekuly lysozymu je tedy

Při teplotě tedy dostaneme dle Difuze (4) odhad rychlosti

(5)

Pokud by molekule lysozymu nebyly kladeny žádné překážky v pohybu, urazila by průměrně více než 13 metrů za 1 sekundu. Protože však protein není ve vakuu, ale ve vodním prostředí, nedostane se molekula lysozymu daleko, neboť záhy narazí do molekuly vody a odrazem změní směr pohybu. Je tak nucena se pohybovat způsobem, který matematicky popisujeme jako náhodnou procházku. Pokud by větší množství takových částic bylo na počátku koncentrováno v malé oblasti, postupem času by se částice pohybovaly v různých směrech a šířily by se do prostoru. Tento jev nazýváme difuzí.

Abychom dokázali matematicky popsat proces difuze, omezíme požadavky modelu difuze jen na nezbytné minimum. Budeme tak předpokládat, že částice se mohou pohybovat pouze podél jedné prostorové osy, Na počátku pozorování, v čase jsou všechny částice v bodě a následně se jejich pohyb řídí zobecněnou náhodnou procházkou s následujícími pravidly:

1. Každá částice se pohybuje rychlostí a jednou za čas se na ose posune o vzdálenost buď vpravo, anebo vlevo, Pro jednoduchost přitom a považujeme za konstanty. Reálně by tyto veličiny mohly záviset na velikosti částice, druhu tekutiny (plynu či kapaliny) tvořící zkoumané prostředí a na teplotě.

2. Pravděpodobnosti posunu vpravo i vlevo jsou v každém časovém kroku rovny 1/2. Částice se v tekutině pohybují nezávisle na historii svých trajektorií, po nárazu do molekuly tekutiny mění směr zcela náhodně. Po sobě jdoucí kroky pohybu částic jsou tedy stochasticky nezávislé.

3. Jednotlivé částice se pohybují nezávisle na sobě, nereagují spolu. To je v praxi pravda, pokud suspenze částic je dostatečně zředěná.

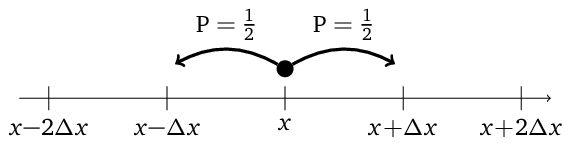
Tato pravidla popisují symetrickou zobecněnou náhodnou procházku, tedy s parametrem Od jednoduché náhodné procházky se liší v tom, že časové a prostorové kroky kroky nemají jednotkovou velikost. Časový krok má délku a částice se na reálné ose pohybují jen po násobcích délky jak je schematicky naznačeno na obr. Difuze 1.

Obr. 1. Schéma symetrické zobecněné náhodné procházky. Za časový interval délky se částice z bodu x přesune buď do bodu x - s pravděpodobností 1/2, anebo do bodu x + , taktéž s pravděpodobností 1/2.

Polohu částice v čase označme jako náhodnou veličinu diskrétního typu. Složením pravidel Difuze i-iii dostáváme rovnici

(6)

kde

(7)

a náhodné veličiny jsou vzájemně stochasticky nezávislé. Lehce spočítáme střední hodnotu a rozptyl náhodné veličiny

	(8)
	(9)

Spojením Difuze (6), Difuze (8) a Difuze (9) nyní spočítáme střední hodnotu a rozptyl polohy částice po jednom časovém kroku,

	(10)
	(11)

Vidíme, že střední poloha částice se v čase nemění, zatímco rozptyl s každým krokem narůstá o konstantní hodnotu

Pro jednoduchost dále předpokládejme, že částici začínáme pozorovat v čase a spočítejme rozptyl její polohy po krocích, tedy v čase Pomocí rekurentního vztahu Difuze (11) lehce spočítáme

(12)

tedy rozptyl polohy částice je přímo úměrný první mocnině času Pokud budou časové kroky dostatečně krátké, zmenší se i délka kroků a zlomek na pravé straně Difuze (12) bude konvergovat k jistému kladnému číslu. Na základě tohoto pozorování se definuje tzv. difuzní koeficient

(13)

pomocí něhož potom můžeme psát Difuzní koeficient charakterizuje pohybové možnosti částic daného typu v určité tekutině při určité teplotě. Obecně proto závisí na velikosti částic, struktuře tekutiny a teplotě. Rozměr veličiny je rovný jednotce plochy dělené jednotkou času, v praxi se často uvádí v

Pro molekuly malých rozměrů ve vodě při pokojové teplotě je difuzní koeficient řádově rovný Při takové hodnotě difuzního koeficientu se částice posune o vzdálenost tj. zhruba délky bakterie, za čas

Urazit krát větší vzdálenost by jí však trvalo

tedy téměř 14 hodin, přesně krát delší čas. Změna polohy není úměrná času, ale jeho druhé odmocnině.

Při difuzi ve vícerozměrném prostoru se pravidla Difuze i-iii použijí pro každou ze souřadnic, příp. Navíc přitom předpokládáme, že průměty pohybu částic do těchto os jsou stochasticky nezávislé. Ve dvourozměrném prostoru tak pro střední kvadratickou vzdálenost od počátku, kdy platí

a ve třírozměrném prostoru, kde pak

Nyní nás bude zajímat rozdělení pravděpodobnosti polohy částice po krocích, tedy v čase

(14)

Použijeme opět matematický popis pomocí Difuze (6) a Difuze (7). Ze znalosti délky časového kroku dokážeme určit, kolik kroků pohybu částice proběhlo, označme tento počet V každém z těchto kroků se náhodná veličina dle Difuze (7) realizovala buď jako posun vpravo o anebo jako posun vlevo o Označme jako náhodnou veličinu počet těch z celkem realizací, které byly posuny vpravo. Podle pravidel Difuze i, Difuze ii je zřejmé, že tato náhodná veličina má binomické rozdělení pravděpodobnosti s parametry a tedy má pravděpodobnostní funkci

(15)

Spočítáme střední hodnotu a rozptyl náhodné veličiny

(16)

Při modelování procesu difuze náhodnou procházkou musíme brát do úvahy, že časový krok musí být dostatečně krátký. Pokud v Difuze (14) položíme počet kroků poroste nade všechny meze. K aproximaci binomického rozdělení za této situace využijeme centrální limitní větu. Ta říká, že rozdělení pravděpodobnosti standardizované náhodné veličiny pro konverguje ke standardizovanému normálnímu rozložení,

Konkrétně, po dosazení Difuze (14) a Difuze (16) pak z vlastností lineární transformace plyne, že rozdělení pravděpodobnosti náhodné veličiny lze pro aproximovat normálním rozdělením

(17)

Pokud při pohybu částice v krocích došlo k posunům vpravo o plyne z předpokladů difuze, že muselo dojít k posunům vlevo. Poloha částice po krocích je tak dána rozdílem

neboli, mezi a existuje jednoznačný lineární vztah

(18)

Ze znalosti rozložení Difuze (17) již nyní lehce dopočítáme asymptotické rozdělení pravděpodobnosti polohy částice

(19)

Za podmínek modelu difuze pomocí náhodné procházky tak poloha částice, v čase má normální rozdělení s nulovou střední hodnotou a rozptylem lineárně závislém na čase a na hodnotě difuzního koeficientu Hustota pravděpodobnosti tohoto rozdělení je rovna

(20)

Podle pravidel Difuze i, Difuze ii se za časový interval jednoho kroku částice do místa mohla dostat s pravděpodobností 1/2 z místa anebo s pravděpodobností 1/2 z místa Použitím formule úplné pravděpodobnosti tak můžeme psát

(21)

Zaveďme pro tyto pravděpodobnosti označení

(22)

Rovnici Difuze (21) přepíšeme do tvaru

(23)

Od obou stran nyní odečteme výraz zlomek na pravé straně rozšíříme výrazem a celou rovnici vydělíme . Po přeuspořádání výrazů na obou stranách dostaneme

(24)

Provedeme limitní přechod tak, aby podíl byl konečný. Na levé straně Difuze (24) tak vznikne první parciální derivace funkce podle času První zlomek na pravé straně je roven difuznímu koeficientu Limita druhého zlomku na pravé straně je rovna druhé parciální derivaci funkce vzhledem k prostorové proměnné jde o hlavní člen tzv. tříbodové formule. Vztah Difuze (24) tak uvedeným limitním přechodem přejde na rovnici

(25)

kterou nazýváme rovnicí difuze. Není náhodou, že tuto parciální diferenciální rovnici splňuje právě hustota normálního rozdělení pravděpodobnosti Difuze (20).