Úvod

Náš výklad řešení rovnice difuze pro jednorozměrný prostor začneme nejjednodušším případem, kdy předpokládáme, že chceme popsat časový vývoj koncentrace částic v jednotlivých místech nekonečně dlouhé trubice. Ačkoliv se na první pohled může zdát, že tato situace je ryze teoretická a pro praxi nepoužitelná, ukazuje se, že je i dobrou aproximací situace, kdy trubice je sice konečné délky, ale ta část trubice, která je zájmem modelování, je natolik vzdálena od konců trubice, že vliv tzv. okrajových podmínek můžeme zanedbat. Matematicky přesné řešení rovnice difuze ponecháme až zcela na závěr, ukáže se tak totiž, jak principiálně jiné a na výpočet mnohem náročnější je přesné řešení s uvažovanými okrajovými podmínkami.

Připomeňme parciální diferenciální rovnici 2. řádu Difuze (34), resp. Difuze (25). V této difuze, nazývané též rovnicí vedení tepla,

(1)

vystupuje jedna prostorová proměnná,  a časová proměnná, Konstanta značí difuzní parametr, který kvantifikuje, jak rychle se částice v uvažovaném objektu (trubici) šíří.

V našem výkladu se nebudeme zabývat řešením uvedené diferenciální rovnice, které je z velké míry založeno na Laplaceově a Fourierově transformaci a jisté dávce praktických zkušeností s využitím těchto integrálních transformací. Zvídavého čtenáře odkazujeme na některou z monografií či skripta o parciálních diferenciálních rovnicích.

Naopak se více zaměříme na interpretaci řešení a vliv parametrů pro několik praktických počátečních, resp. okrajových, úloh. Dále si všimneme, že v řešení většiny úloh určitým způsobem figuruje hustota nebo distribuční funkce normálního (Gaussova) rozdělení pravděpodobnosti. Předpokládáme, že s těmito pojmy se čtenář dosud setkával výhradně v kurzech pravděpodobnosti a matematické statistiky, tedy ve spojení s náhodnými veličinami. Zde však žádná náhoda není, tvar rovnice difuze i počáteční, příp. podmínky, jsou jednoznačně zadány. I přesto hraje normální (Gaussovo) rozdělení velkou roli v řešení rovnice difuze. Základ tohoto možná poněkud překvapivého propojení hledejme v závěrečné části předchozí kapitoly. Právě tam jsme si ukázali dva matematicky ekvivalentní pohledy na difuzi: mikroskopický, založený na náhodné procházce, resp. Brownově pohybu, jednotlivých částic, a makroskopický, popisující koncentraci částic v určitém místě a čase.

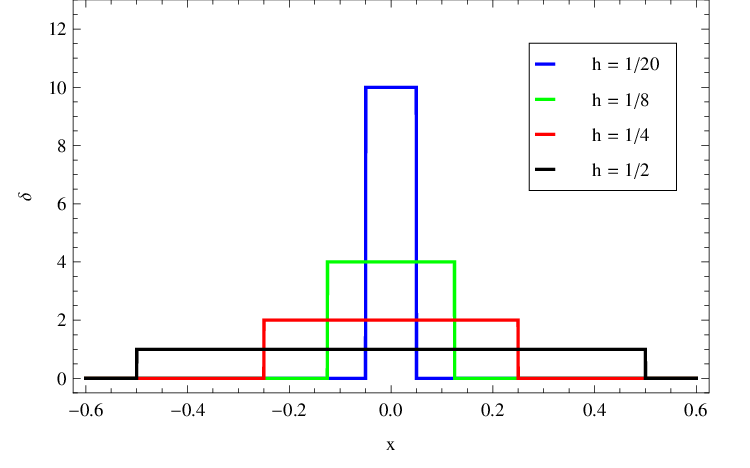
K matematickému popisu některých podmínek budeme potřebovat pojem tzv. Diracovy delta-funkce (či jen delta-funkce)  Jednou z možností je definovat tuto funkci jako limitu hustoty pravděpodobnosti rovnoměrného rozdělení pravděpodobnosti na intervalu pro

(2)

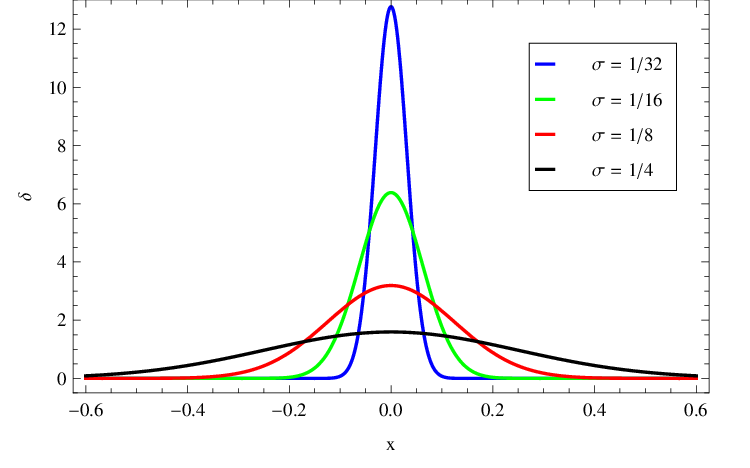
Alternativní definice Diracovy delta-funkce je ve tvaru hustoty pravděpodobnosti singulárního normálního rozdělení pravděpodobnosti, tedy jako limitní případ normálního rozdělení se střední hodnotou a s rozptylem konvergujícím k nule,

(3)

Z obou definic je patrné, že Diracova delta-fukce není funkcí v klasickém pojetí, neboť pro nabývá nekonečné hodnoty (není reálným číslem),

(4)

Navzdory nekonečné hodnotě integrandu v jednom bodě však v důsledku definic založených na hustotách pravděpodobnosti pro Lebesgueův integrál delta-funkce platí

(5)

Při řešení rovnice difuze za různých podmínek budeme dále využívat následující vlastnost delta-funkce, nazývanou ampling property. Pro spojitou funkci platí

(6)

tedy integrál součinu funkce s delta-funkcí je rovný hodnotě této funkce v bodě

Obr. 1. Schéma konvergence hustoty rovnoměrného rozdělení k delta-funkci. Obsah obdélníka je stále rovný jedné, při zmenšující se šířce (2 h) tak jeho výška (1/2 h) konverguje k nekonečnu.

Obr. 2. Schéma konvergence hustoty normálního rozdělení k delta-funkci. Obsah plochy pod křivkou je stále rovný jedné, rozptyl však klesá k nule.

Pro přehlednost a zjednodušení zápisu budeme v celé této kapitole dále používat značení pro hustotu centrovaného normálního rozdělení pravděpodobnosti s rozptylem

(7)

a pro odpovídají distribuční funkci,

(8)