Trubice s trvalým zdrojem na okraji

Dalším, v praxi častým, typem úlohy je difuze v trubici, na jejímž okraji je po celou dobu experimentu udržována předepsaná konstantní koncentrace částic, které jsou na okraji technickým zařízením dodávány, nebo naopak odčerpávány. Řešíme tedy difuzní rovnici Řešení rovnice difuze, 2. část (1) pro s počáteční podmínkou

(13)

a okrajovou podmínkou

(14)

Difuzní rovnice má za těchto podmínek řešení

(15)

přičemž označuje distribuční funkci Řešení rovnice difuze (8). Výraz v hranatých závorkách v Řešení rovnice difuze, 2. část (15) je tedy funkcí přežití a grafem závislosti koncentrace na je -násobek pravé poloviny grafu funkce přežití normálního rozdělení.

Průběh koncentrace částic odpovídající řešení této úlohy je zobrazeno na grafu v obr. Řešení rovnice difuze, 2. část 5. Pozorujeme, že na okraji je, v souladu s okrajovou podmínkou, koncentrace částic konstantní v čase. Rozložení koncentrace v trubici v několika časových okamžicích je zachyceno v obr. Řešení rovnice difuze, 2. část 6. Prostorová rozložení koncentrace mají tvar konvexních funkcí klesajících z hodnoty asymptoticky k nule.

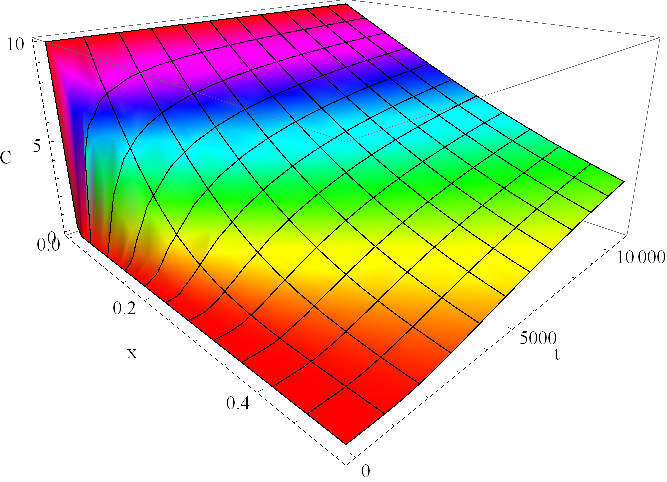Obr. 5. Koncentrace C(x,t) v mM dle Řešení rovnice difuze, 2. část (15) v závislosti na prostorové souřadnici v cm a na čase v sekundách. Na okraji ( x = 0 ) je stále udržována koncentrace částic na hodnotě C0 = 10-5 mol cm-3. Difuzní koeficient má hodnotu D = 10-5 cm2 s-1.

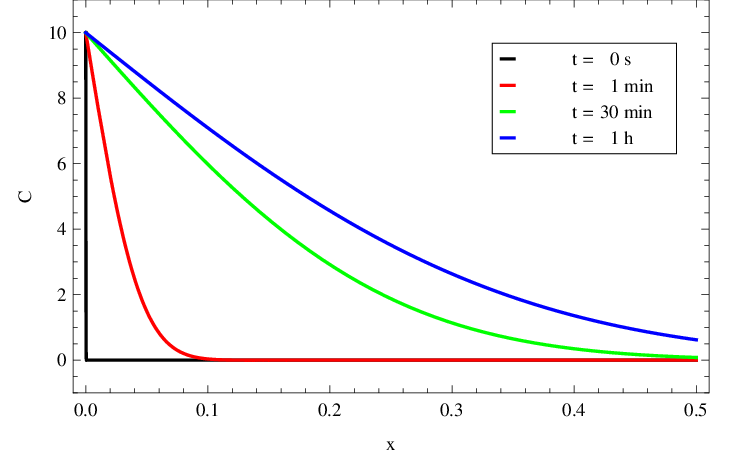Obr. 6. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze, 2. část 5 v závislosti na (v cm) v několika časových okamžicích.