Trubice s bodovým zdrojem a nulovou koncentrací na okrajích

Jako poslední z úloh na řešení jednodimenzionální rovnice difuze si ukážeme řešení pro trubic konečné délky a tedy se specifikovanými dvěma okrajovými podmínkami. Tato úloha, ač možná z prvního pohledu prakticky nejčastější, je z matematického hlediska mnohem složitější, než všechny předchozí. Současná specifikace obou okrajových podmínek, tedy hodnot koncentrace ve dvou bodech, je značně omezující a řešení takové úlohy je tak možné pouze ve tvaru Fourierovy řady, tedy nekonečné řady goniometrických funkcí.

Uvažujeme trubici délky jejíž jeden konec pro jednoduchost umístíme do počátku souřadnicového systému. Prostorovou souřadnici tedy uvažujeme v intervalu Předpokládáme, že počáteční koncentrace částic v trubici je popsána funkcí

(16)

a že koncentrace částic na obou koncích trubice je trvale udržována na nulové hodnotě,

(17)

Difuzní rovnice Řešení rovnice difuze, 2. část (1) s počáteční podmínkou Řešení rovnice difuze, 2. část (16) a okrajovými podmínkami Řešení rovnice difuze, 2. část (17) má řešení

(18)

ve tvaru Fourierovy řady, nekonečné řady funkcí, kde jsou za bázové funkce voleny goniometrické funkce (zde konkrétně sinus) s proměnlivými periodami.

Pro jednoduchost uvažujme opět speciální případ, kdy na počátku jsou vypuštěno množství částic v místě uprostřed trubice,

(19)

Integrály v Řešení rovnice difuze, 2. část (18) jsou pak rovny

a řešení této speciální úlohy je ve tvaru nekonečné řady

(20)

Graf řešení Řešení rovnice difuze, 2. část (20) je zobrazen v obr. Řešení rovnice difuze, 2. část 7. Při numerických výpočtech je nutno vzít dostatečně členů nekonečné řady, řádově několik set, aby na grafu koncentrace nebyly patrné artefakty vlnění o vysoké frekvenci v důsledku skládání řešení z goniometrických funkcí. Rozložení koncentrace v trubici v několika časových okamžicích je zachyceno v obr. Řešení rovnice difuze, 2. část 8. Krátce po začátku je rozložení podobné Gaussově křivce s chvosty rovnými nule na okrajích trubice. S narůstajícím časem se tvar postupně mění na tvar vlny jakožto části průběhu goniometrických funkcí. Časové vývoje koncentrace v několika místech trubice jsou zachyceny v obr. Řešení rovnice difuze, 2. část 9. Uprostřed trubice, tzn. v bodě koncentrace exponenciálně klesá, v jiných částech trubice nejdříve roste, později také pozvolna klesá. Nejvyšší koncentrace je v každém časovém okamžiku uprostřed trubice, směrem k okrajům trubice klesá, na okrajích je v souladu s okrajovými podmínkami Řešení rovnice difuze, 2. část (17) udržována nulová hodnota.

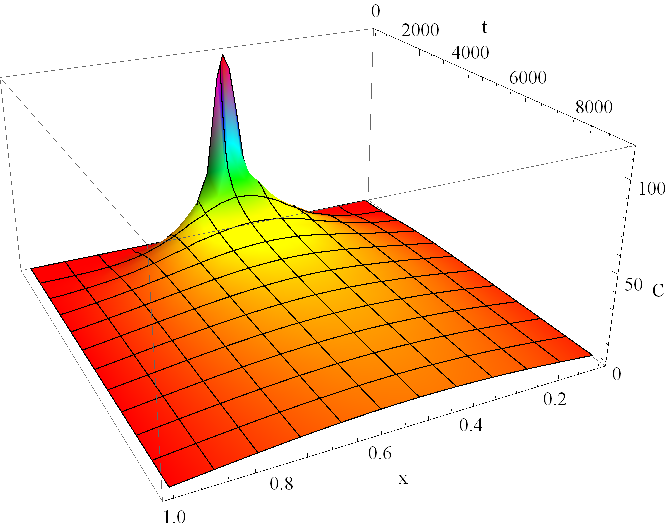Obr. 7. Koncentrace C(x,t) v mM dle Řešení rovnice difuze, 2. část (20) v závislosti na prostorové souřadnici v cm a na čase v sekundách v trubici jednotkové délky, L = 1 cm. Okrajové podmínky stanovují nulovou koncentraci na obou okrajích, počáteční podmínkou je dáno množství N0 částic vložených v čase t = 0 do středu trubice, tedy místa  x = L/2 = 0,5 cm. Trubice má průřez o obsahu S = 0,1 cm2, difuzní koeficient má hodnotu D = 10-5 cm2 s-1.

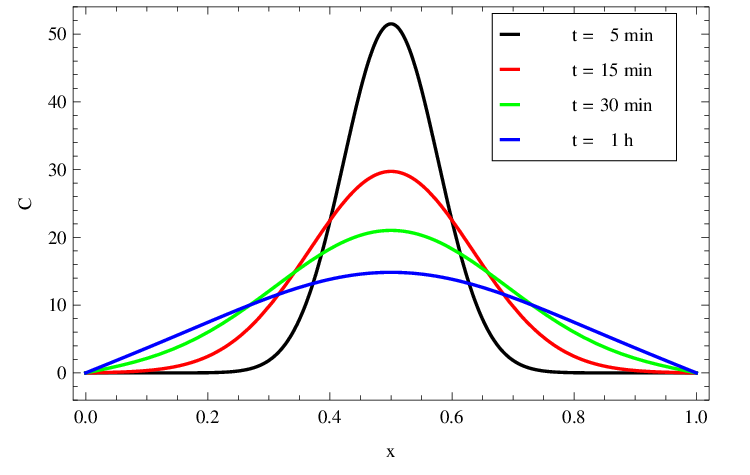Obr. 8. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze, 2. část 7 v závislosti na (v centimetrech) v několika časových okamžicích. Na počátku má rozložení koncentrace přibližně tvar Gaussovy funkce, s rostoucím časem se postupně mění na tvar půlvlny grafy goniometrických funkcí, avšak vždy s nulovými hodnotami na obou okrajích.

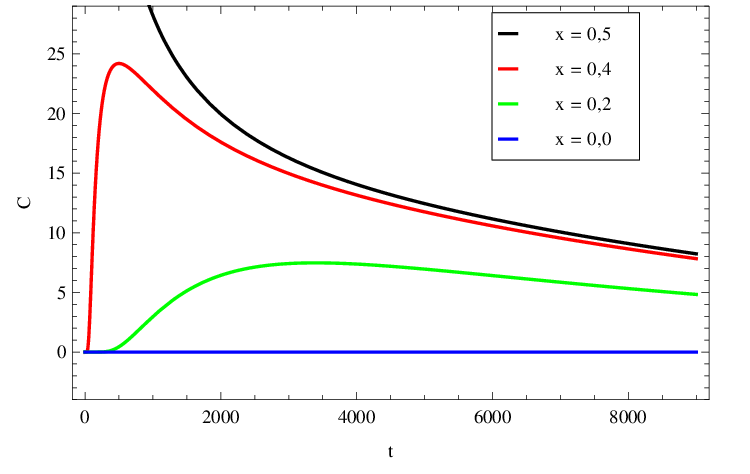Obr. 9. Vývoj koncentrace C(x,t) v mM z obr. Řešení rovnice difuze, 2. část 7 v čase, t, (v sekundách) v několika místech trubice, (v centimetrech). V pravé části trubice jsou průběhy symetrické vzhledem ke středu trubice. Na obou okrajích, tzn pro x = 0 cm a x = L = 1 cm, je koncentrace nulová.