Nekonečná trubice

Uvažujeme nekonečně dlouhou trubici, přičemž počáteční koncentrace částic v ní je popsána funkcí

(9)

Difuzní rovnice Řešení rovnice difuze (1) pro s počáteční podmínkou Řešení rovnice difuze (9) má řešení

(10)

Všimněme si, že člen s odmocninou a exponenciální funkce má tvar hustoty normálního rozdělení pravděpodobnosti se střední hodnotou a rozptylem V souladu se zavedeným označením Řešení rovnice difuze (7) tedy lze psát

(11)

Všimněme si rozměrů zde vystupujících veličin. Délkové míry budeme uvádět v centimetrech a čas v sekundách. Koncentrace a mají rozměr což odpovídá chemické jednotce molární koncentrace Veličina Řešení rovnice difuze (7) vystupující v Řešení rovnice difuze (11) pak musí mít rozměr Zdůrazněme, že hustota pravděpodobnosti není bezrozměrnou veličinou, v praxi má vždy rozměr rovný převrácené hodnotě jednotky veličiny v argumentu hustoty, v našem případě délky. Teprve její integrál, distribuční funkce Řešení rovnice difuze (8), je bezrozměrnou veličinou nabývající hodnot z intervalu

Uvažujme dále speciální případ počáteční podmínky

(12)

kdy, v jinak prázdné trubici s plochou průřezu je v čase vypuštěno částic v místě trubice. Množství částic předpokládáme uváděné v molech, plochu průřezu trubice v tedy delta-funkce musí mít rozměr Je to v souladu s definicí delta-funkce jako limitního případu hustoty pravděpodobnosti. Delta-funkce v počáteční podmínce určuje prostorovou polohu zdroje na -ové ose, má tedy rozměr převrácené hodnoty jednotky délky. Dosadíme Řešení rovnice difuze (12) do Řešení rovnice difuze (11) a obdržíme

(13)

což s využitím Řešení rovnice difuze (6) dává řešení

(14)

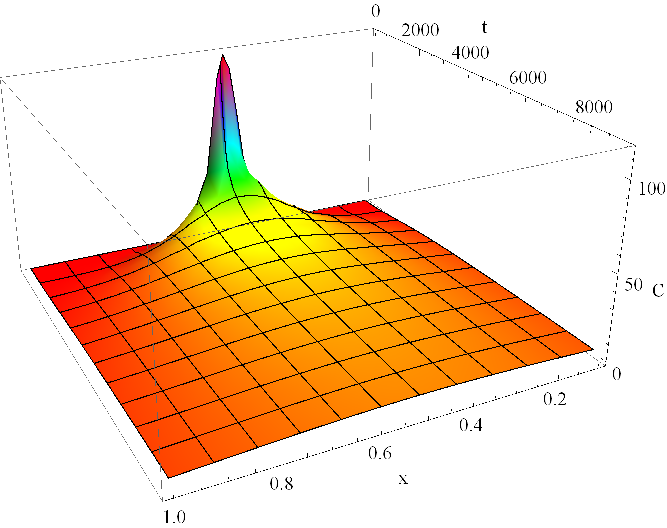
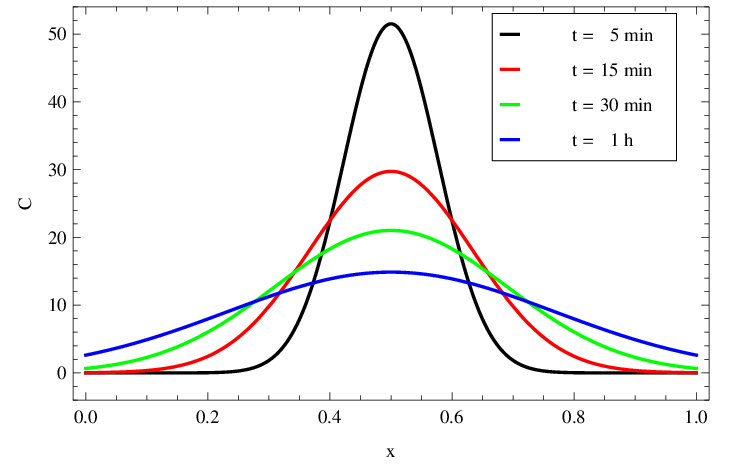
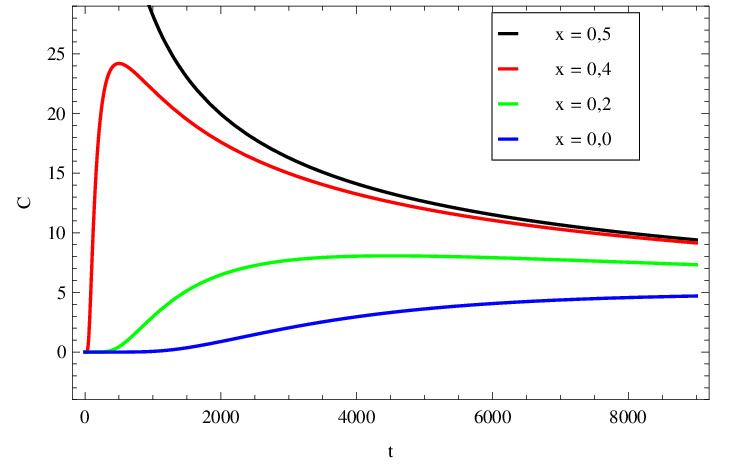
ve tvaru -násobku hustoty normálního rozdělení se střední hodnotou a rozptylem Graf řešení je je zobrazen v obr. Řešení rovnice difuze 3. Rozložení koncentrace v trubici v několika časových okamžicích je zachyceno v obr. Řešení rovnice difuze 4. Koncentrace má v každém čase přesně tvar hustoty normálního rozdělení se střední hodnotou a rozptylem lineárně rostoucím v čase. Časové vývoje koncentrace v několika místech trubice jsou zachyceny v obr. Řešení rovnice difuze 5. V místě zdroje, v trubici koncentrace exponenciálně klesá, v ostatních místech nejdříve roste a později klesá. Nejvyšší koncentrace je vždy v místě zdroje, směrem od tohoto místa symetricky klesá.

Obr. 3. Koncentrace C(x,t) v mM = 10-6 mol cm-3 dle Řešení rovnice difuze (14) v závislosti na prostorové souřadnici v cm a na čase v sekundách. Na počátku je v místě a=0,5 cm vypuštěno N0 = 10-6 mol částic, jejichž difuzní koeficient je roven D = 10-5 cm2 s-1. Trubice má konstantní průřez o ploše S = 0,1 cm2.

Obr. 4. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze 3 v závislosti na x (v cm) dle Řešení rovnice difuze (14) v několika časových okamžicích.

Obr. 5. Vývoj C(x,t) v mM z obr. Řešení rovnice difuze 3 v čase (v sekundách) dle Řešení rovnice difuze (14) v čase t v několika místech (v centimetrech) trubice.

Uvažujme další příklad, se dvěma počátečními zdroji, s  částicemi v bodě a s částicemi v bodě trubice.
Řešíme tedy Řešení rovnice difuze (1) na s počáteční podmínkou

(15)

Parciální diferenciální rovnice difuze je lineární, tzn. pro řešení platí tzv. princip superpozice. Při lineární kombinaci počátečních podmínek získáme řešení stejnou kombinací řešení, které odpovídají jednotlivým počátečním podmínkám. V tomto případě tedy zkombinujeme dvě řešení tvaru Řešení rovnice difuze (14) a obdržíme řešení úlohy Řešení rovnice difuze (1), Řešení rovnice difuze (15) ve tvaru

(16)

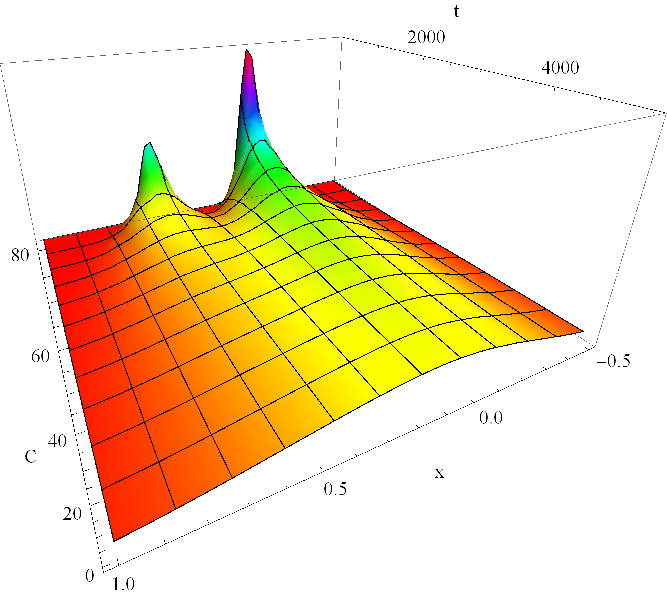
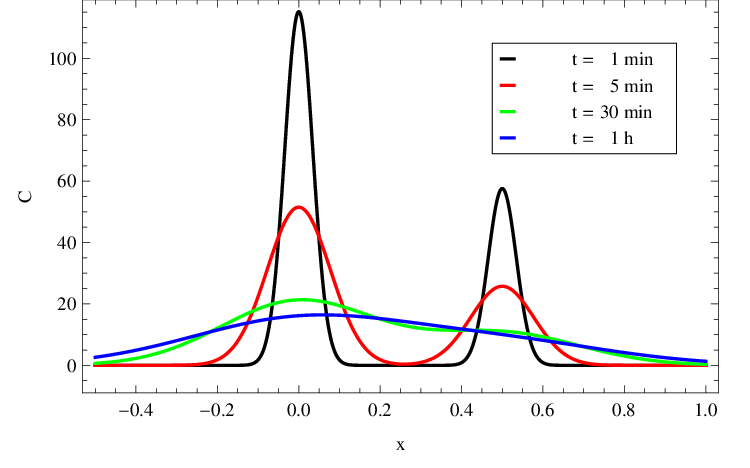
Jeho průběh je zobrazen na grafu v obr. Řešení rovnice difuze 6. Rozložení koncentrace v trubici v několika časových okamžicích je zachyceno v obr. Řešení rovnice difuze 7. Řešení Řešení rovnice difuze (16) je směsí násobků hustot normálních rozdělení se středními hodnotami a a s rozptyly lineárně rostoucími v čase. Prostorový průběh koncentrace se postupně vyhlazuje, po určitém čase (v závislosti na vzdálenosti zdrojů) dojde ke změně z bimodálního tvaru na tvar unimodální.

Obr. 6. Koncentrace C(x,t) v mM dle Řešení rovnice difuze (16) v závislosti na prostorové souřadnici v cm a na čase v sekundách. Na počátku je v místě a1 = 0 cm vypuštěno N1 = 10-6 mol částic a v místě a2 = 0,5 cm množství N2 = 0,5 . 10-6 mol částic, jejichž difuzní koeficient je roven D = 10-5 cm2 s-1. Trubice má konstantní průřez o ploše S = 0,1 cm2.

Obr. 7. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze 6 v závislosti na x (v cm) v několika časových okamžicích.

Předchozí úlohu se dvěma zdroji lze principem superpozice zobecnit na případ nejvýše spočetně mnoha zdrojů, které na počátku pozorování vypustí požadované koncentrace částic v daných místech trubice. Řešení Řešení rovnice difuze (16) pak bude tvořeno součtem hodnot hustot rozdělení pravděpodobnosti násobených plošnými koncentracemi