Trubice s podélným zdrojem a nulovým tokem na okraji

Počáteční podmínku bodového zdroje na trubici s nulovým tokem na okraji opět rozšíříme na podélný zdroj o koncentraci v intervalu mezi body a Sudé rozšíření této počáteční podmínky,

(10)

je rovné

(11)

Po prostudování předchozích kapitoly již čtenář patrně intuitivně očekává tvar řešení difuzní rovnice Řešení rovnice difuze, 2. část (1) pro s počáteční podmínkou Řešení rovnice difuze, 2. část (10) a okrajovou podmínkou Řešení rovnice difuze, 2. část (3),

(12)

ve tvaru kombinace hodnot distribučních funkcí normálních rozdělení se středními hodnotami a stejným rozptylem
Rozdíl od Řešení rovnice difuze (32) je jen v opačných znaménkách zdánlivého zdroje. Formální výpočet spočívá v dosazení Řešení rovnice difuze, 2. část (11) do Řešení rovnice difuze, 2. část (5),

následné substituci v obou integrálech a využití Řešení rovnice difuze (8). Detaily tohoto výpočtu a úpravu na tvar Řešení rovnice difuze, 2. část (12) již ponecháváme čtenáři jako cvičení.

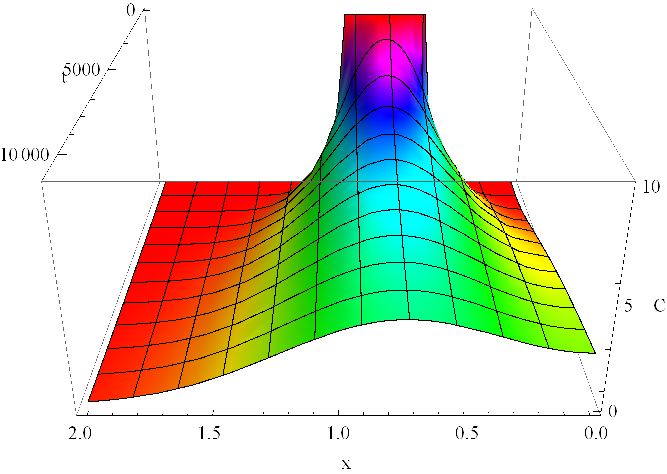
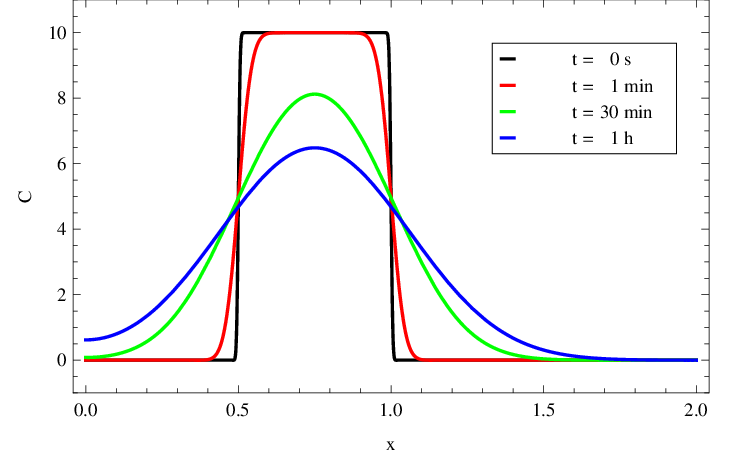
Řešení je zobrazeno na grafu v obr. Řešení rovnice difuze, 2. část 3, rozložení koncentrace v trubici v několika časových okamžicích je pak zachyceno v obr. Řešení rovnice difuze, 2. část 4. Je vidět postupné vyhlazování prostorového rozložení s rostoucím časem. Současně je patrné dosažení lokálního extrému prostorových průběhů koncentrací v bodě tedy nulovost toku na okraji.

Obr. 3. Koncentrace C(x,t) v mM dle Řešení rovnice difuze, 2. část (12) v závislosti na prostorové souřadnici  v cm a na čase v sekundách. Okrajovou podmínkou je stanoven nulový tok na okraji, na počátku jsou do části trubice mezi body a = 0,5 cm a b = 1 cm vloženy částice o koncentraci C0 = 10-5 mol cm-3. Průřez trubice má obsah S = 0,1 cm2, difuzní koeficient má hodnotu D = 10-5 cm2 s-1.

Obr. 4. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze, 2. část 3 v závislosti na (v cm) v několika časových okamžicích. Koncentrace na okraji není obecně nulová, ale vzhledem k prostorové proměnné zde má nulovou derivaci.