Nekonečná trubice s podélným zdrojem

Jak se řešení Řešení rovnice difuze (16) změní, když budou zdroje rozmístěny v nespočetně mnoha bodech trubice? Představme si, že na počátku bude zajištěna koncentrace částic v celém úseku trubice mezi dvěma body, a , Hledáme tedy řešení difuzní rovnice Řešení rovnice difuze (1) pro s počáteční podmínkou

(17)

I v tomto případě lze díky linearitě difuzní rovnice využít princip superpozice. Nyní však součet hodnot hustot v nespočetně mnoha bodech přejde v integrál hustoty rozdělení v uvedených mezích,

(18)

Z vlastností spojitých náhodných veličin víme, že určitý integrál hustoty pravděpodobnosti je roven rozdílu hodnot distribuční funkce, řešení difuzní rovnice s podélným počátečním zdrojem tak lze zapsat také ve tvaru

(19)

s distribuční funkcí podle Řešení rovnice difuze (8). Opět připomeňme rozměry veličin. Koncentrace i mají jednotky distribuční funkce je bezrozměrnou veličinou. Pokud bychom počáteční koncentraci chtěli specifikovat pomocí množstvím částic, podobně jako u bodového zdroje, můžeme psát

Tento zápis však v praxi není obvyklý, zejména proto, že umožňuje pracovat jen se zdrojem konečné délky

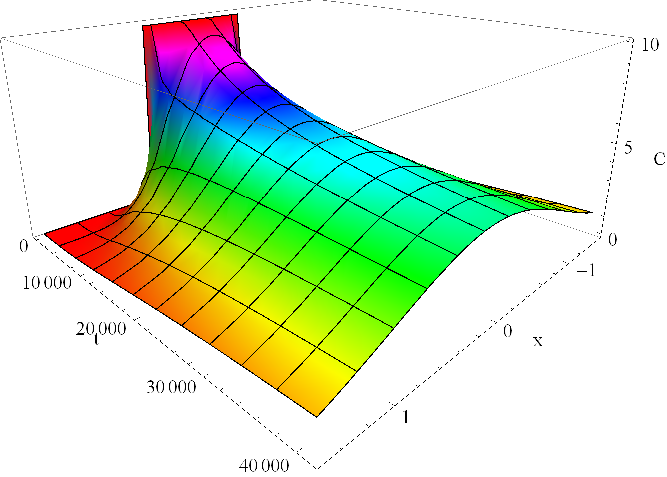Obr. 8. Koncentrace C(x,t) v mM dle Řešení rovnice difuze (19) v závislosti na prostorové souřadnici v cm a na čase v sekundách. Na počátku je mezi body a = -0,5 cm a b = 0,5 cm koncentrace částic rovna C0 = 10-5 mol cm-3. Difuzní koeficient je roven D = 10-5 cm2 s-1.

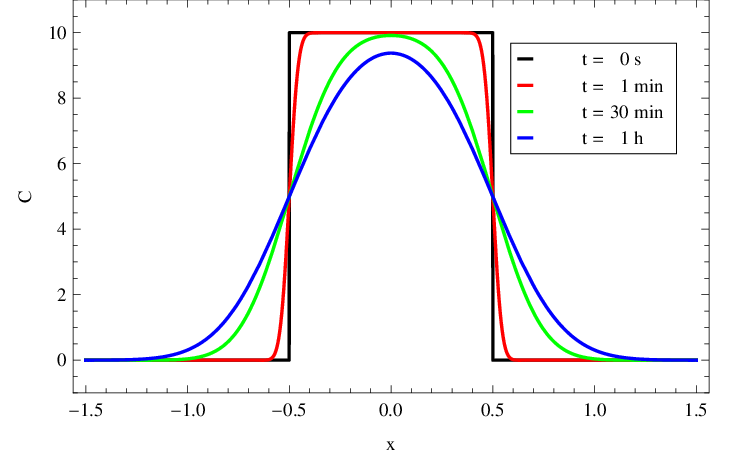Obr. 9. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze 8 v závislosti na x (v  cm) v několika časových okamžicích.

Průběh řešení je zachycen v grafu v obr. Řešení rovnice difuze 8. Rozložení koncentrace v trubici v několika časových okamžicích je pak zobrazeno v obr. Řešení rovnice difuze 9. V čase je rovno počáteční podmínce ve tvaru funkce se skoky v bodech a Pro je již rozložení koncentrace hladkou funkcí ve tvaru rozdílu hodnot distribuční funkce regulárního normálního rozdělení pravděpodobnosti. S rostoucím časem se tvar řešení dále více vyhlazuje, neboť roste rozptyl

Počáteční úlohu nyní zobecníme na nekonečně dlouhý počáteční zdroj, který je umístěn podél trubice od daného bodu Uvažujeme tedy počáteční podmínku ve tvaru

(20)

Tato skoková funkce je (pro ) známá pod názvem Heavisideova funkce (zprava spojitá). Řešení počáteční úlohy Řešení rovnice difuze (1), Řešení rovnice difuze (20) lehce obdržíme z řešení Řešení rovnice difuze (18) limitním přechodem

(21)

Vidíme, že řešením je -násobek hodnoty distribuční funkce normálního rozdělení pravděpodobnosti se střední hodnotou a rozptylem

Průběh řešení je pro volbu zachycen v grafu v obr. Řešení rovnice difuze 10. Rozložení koncentrace v trubici v několika časových okamžicích je pak zobrazeno v obr. Řešení rovnice difuze 11. Vidíme tvary distribuční funkce normálního rozdělení s rozptylem lineárně rostoucím v čase. Počáteční podmínce odpovídající Heavisideova funkce je také distribuční funkcí, a to tzv. singulárního normálního rozdělení pravděpodobnosti (jemu odpovídající hustota je -funkce). Již nás nepřekvapí, že s rostoucím časem se počáteční rozložení koncentrace částic v trubici vyhlazuje.

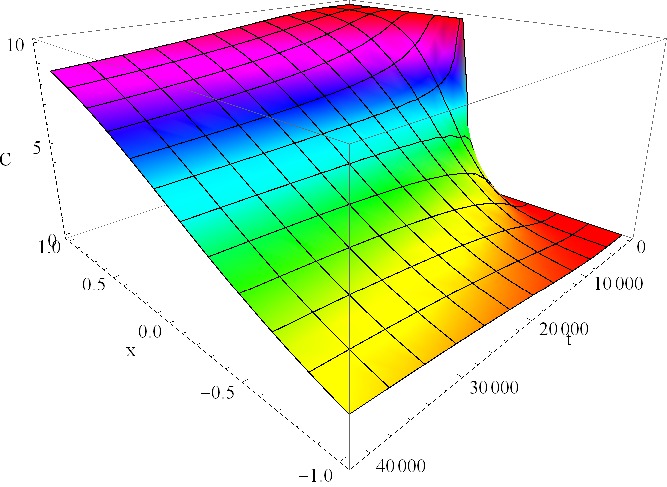Obr. 10. Koncentrace C(x,t) v mM dle Řešení rovnice difuze (21) v závislosti na prostorové souřadnici v cm a na čase v sekundách. Parametry mají hodnoty a=0 cm, C0=10-5 mol cm-3, D=10-5 cm2 s-1.

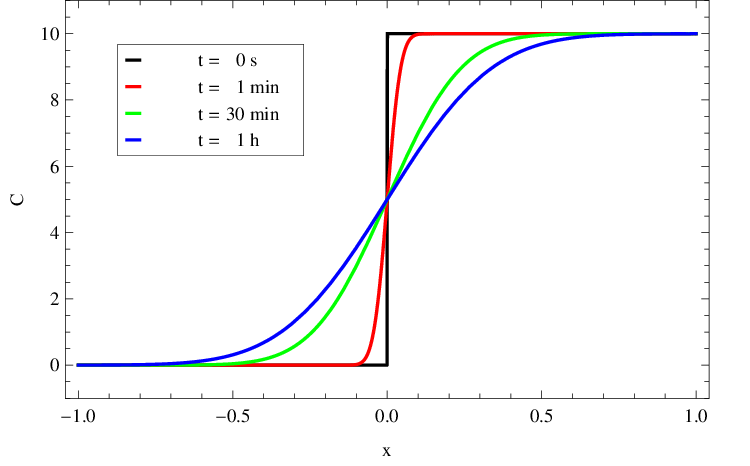Obr. 11. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze 10 v závislosti na x (v cm) v několika časových okamžicích.