Statistické vlastnosti jádrových odhadů

Kvalitu jádrového odhadu lze lokálně popsat pomocí střední kvadratické chyby odhadu v bodě  která je obecně dána vztahem  

Upravíme tento vztah

		(5)

což znamená, že střední kvadratická chyba může být vyjádřena jako součet rozptylu odhadu  a čtverce vychýlení Tento rozklad rozptyl-vychýlení usnadňuje analýzu vlastností odhadu.

Všechny uvedené jádrové odhady regresní funkce jsou asymptoticky ekvivalentní (viz např. [8, 14]). Z tohoto důvodu budeme dále podrobněji zabývat Priestleyovými-Chaovými odhady, které budeme psát bez uvedení označení , tedy: a

Připomeňme, že pro Priestleyovy-Chaovy odhady je váhová funkce tvaru 

Pro další výpočty budeme předpokládat:

(i)	Jádrová funkce je sudou funkcí na intervalu [-1,1],
(ii)	vyhlazovací parametr je nenáhodnou posloupností kladných čísel splňující  a pro
(iii)	bod v němž počítáme odhad, splňuje nerovnost pro všechna  kde je pevné,
(iv)
(v)

Je zřejmé, že pro platí (jedná se o přibližný výpočet integrálu - viz Dodatek této kapitoly a Symbolika  a )

		(6)

Nechť odtud a tedy s využitím Taylorova rozvoje

		(7)

Podle výše uvedených předpokladů platí tedy a pro  Odtud, s využitím faktu, že nosičem funkce je interval [-1,1], plyne

Celkem dostaneme

Podobně pro rozptyl platí

z vlastností Jádrové odhady regresní funkce (2) plyne  pro  tedy

Zde jsme opět použili přibližného výpočtu integrálu. Opět s využitím substituce a vztahu můžeme pro psát

Tímto jsme dokázali následující větu o tvaru střední kvadratické chyby.

Věta 3.1. Nechť jsou splněny předpoklady (i)-(iii), pak střední kvadratická chyba nabývá tvaru

(8)

Chyba dává pouze lokální pohled na chybu odhadu, proto se častěji používá globální tvar chyby -  - asymptotická střední integrální kvadratická chyba. je součástí střední integrální kvadratické chyby a vztah mezi chybami a je následující

je tvaru

(9)

kde a značí asymptotický tvar rozptylu (asymptotic integrated variance) a  asymptotický tvar druhé mocniny vychýlení (asymptotic integrated square bias).

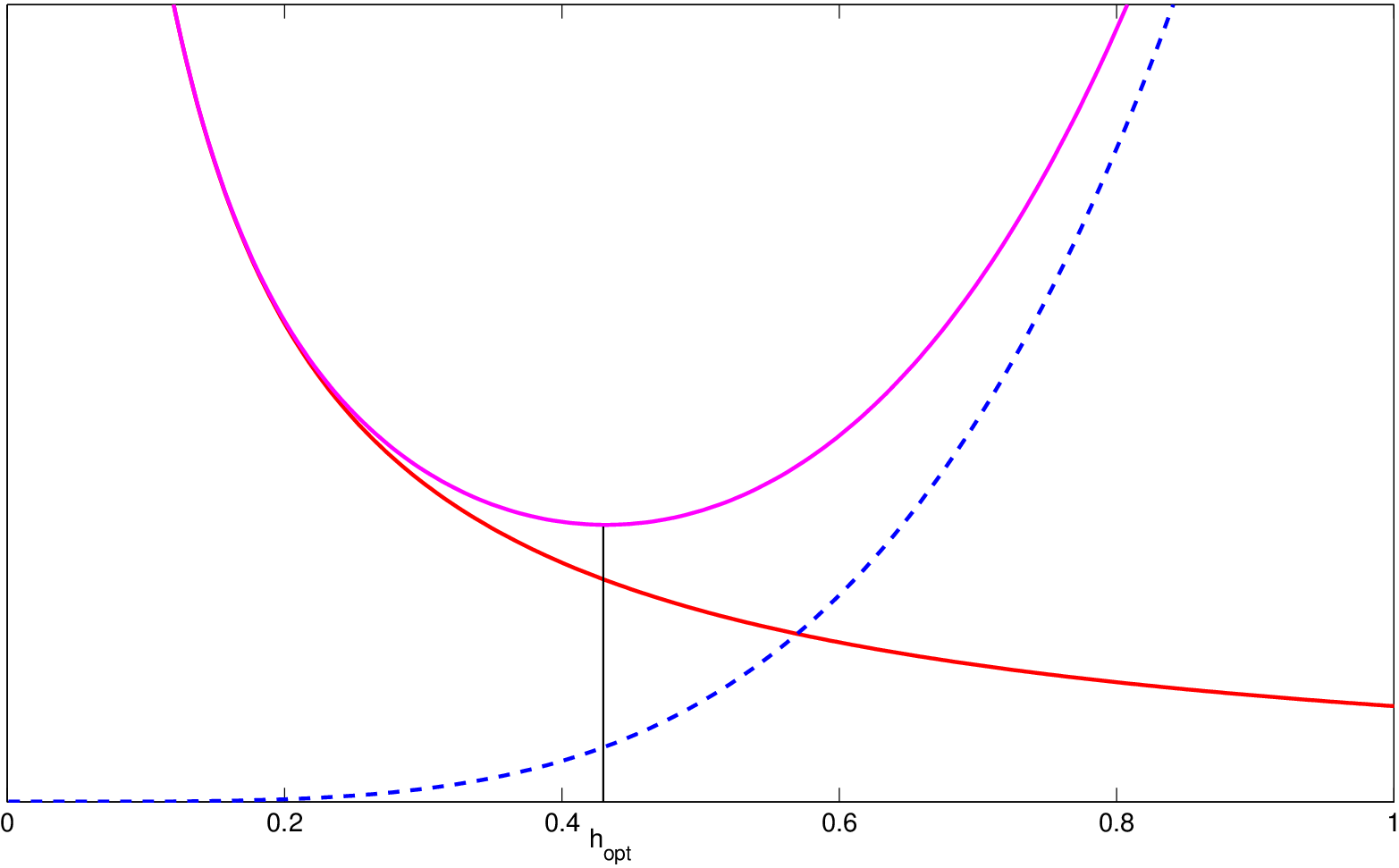Obr. 9. AMISE (růžová, plná) jako součet rozptylu AIV (červená, plná) a vychýlení AISB (modrá, čárkovaná)

Na obrázku je znázorněn průběh a a také výsledné chyby  Je vidět, že rozptyl nabývá velkých hodnot pro malé, ale  klesá. Pro velké je tomu naopak. Volba vyhlazovacího parametru je zřejmě klíčovým problémem jádrového vyhlazování.

Naším cílem je minimalizovat  tzn. najít takovou hodnotu vyhlazovacího parametru  pro kterou asymptotická střední integrální kvadratická chyba nabývá minimální hodnoty, a tedy odhad bude nejlepší ve smyslu . Užijeme metody matematické analýzy a spočítáme derivaci

položíme ji rovnu nule a vyjádříme 

(10)

Poznámka 3.2. Tento výpočet vede k nalezení minima  protože platí

Vztah Jádrové odhady regresní funkce (10) má pouze teoretický charakter, protože hodnota závisí na neznámých veličinách a a tedy není užitečná pro praktické účely. Abychom odhadli optimální hodnotu vyhlazovacího parametru, musíme použít metody, které jsou založeny na datech (data-driven methods). Nejznámější z těchto metod bude uvedena v dalším odstavci.

Vztah Jádrové odhady regresní funkce (10) pro optimální šířku vyhlazovacího okna ukazuje, že řád konvergence optimální šířky vyhlazovacího okna závisí na řádu jádra tedy pro jádra řádu je  Dosadíme-li Jádrové odhady regresní funkce (10) do vztahu Jádrové odhady regresní funkce (9) pro  dostaneme

		(11)

tj. 

Poznámka 3.3. Jestliže jádro náleží do třídy pak je tvaru

(12)

a pro optimální vyhlazovací parametr platí

(13)

kde podrobněji např. [7].

Nyní uvedeme důležité lemma, které ukazuje zajímavou vlastnost vyhlazovacího parametru.

Lemma 3.4. Pro platí

Důkaz. Viz Cvičení 6.

Lze ukázat, že pro jádra je To znamená, že s rostoucím se zvyšuje asymptotická rychlost konvergence. Ale není zcela jasné, zda tato zvýšená rychlost konvergence vede již k zlepšení pro konečné rozsahy výběrů, neboť ostatní veličiny se rovněž mění s . Nevýhodou jader vyšších řádů je fakt, že pro tato jádra je optimální šířka okna větší, což může mít negativní dopad na hraniční efekty [9]. Na druhé straně, chování jádrových odhadů s jádry vyšších řádů je méně citlivé na volbu šířky okna, není-li určena zcela optimálně, neboť křivka je plošší.

Poznámka 3.5. Vyšetřování kvality odhadu obvykle probíhá za předpokladu, že pracujeme s vnitřními body intervalu [0,1]. V hraničních oblastech, tj. v intervalech je kvalita odhadu ovlivněna negativně skutečností, že jádro zde nesplňuje momentové podmínky Jádrové funkce a jejich vlastnosti 1.1. To je způsobeno tím, že blízko krajních bodů nosič jádra zasahuje do oblasti, kde nejsou žádná data, což zhoršuje odhad - viz nasledující obrázek.

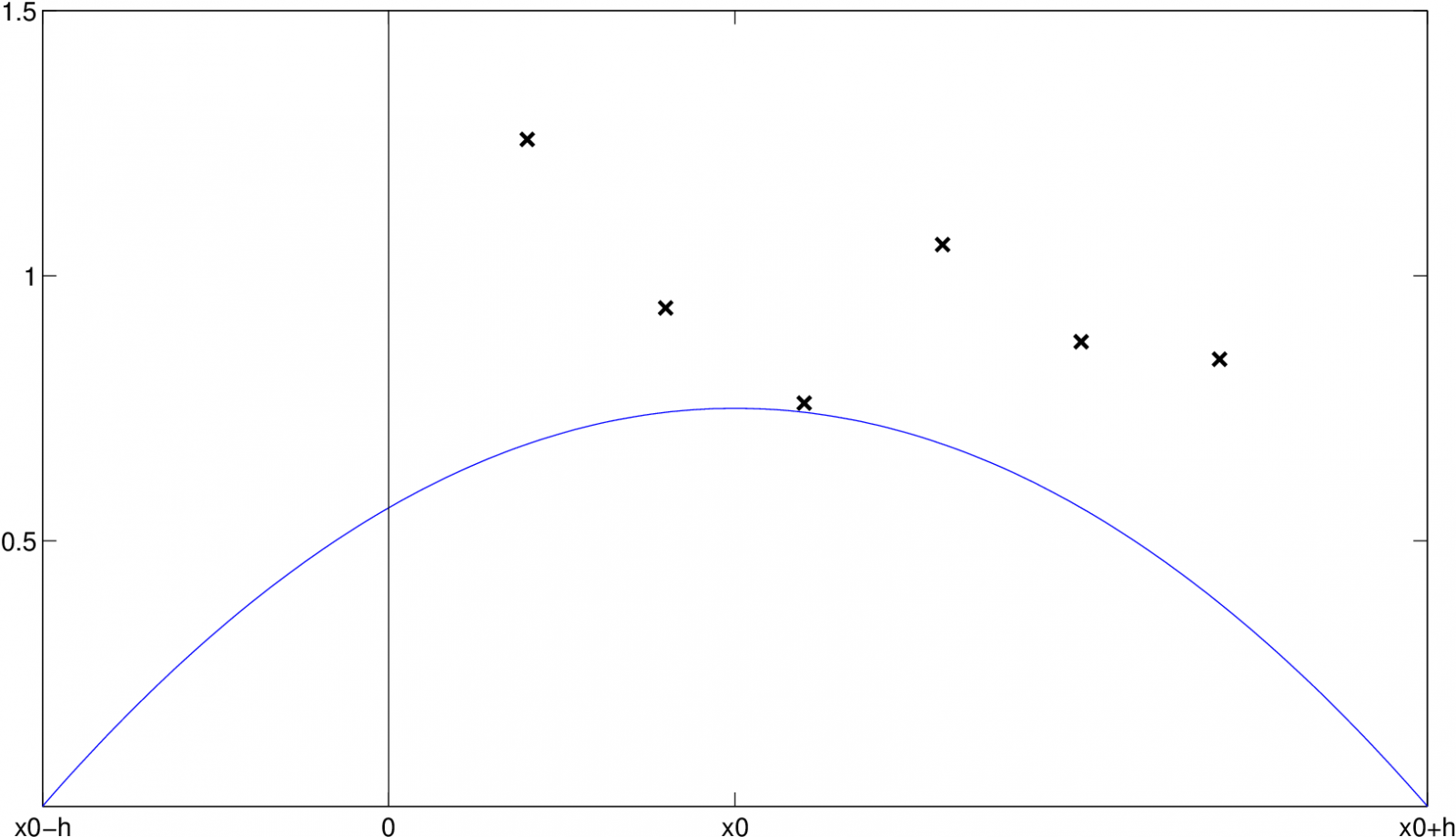Obr. 10. Hraniční efekt

 Hraniční efekty jsou také patrné na obrázcích Jádrové odhady regresní funkce 7a) a Jádrové odhady regresní funkce 10, zejména u pravého okraje intervalu. Problém okrajových efektů lze překonat např. použitím hraničních jader (viz [9]) nebo reflexní metodou (viz [3]).

Příklad 3.6. Uvažujme simulovaná data generovaná regresní funkcí na intervalu  s chybami  Vypočítejme hodnotu optimálního vyhlazovacího parametru pro odhad s jádrem řádu 2.

Podle vztahu Jádrové odhady regresní funkce (10) potřebujeme spočítat výraz

Výpočet pro

• Epanečnikovo jádro:

• obdélníkové jádro: 

Odhady s optimálním vyhlazovacím parametrem pro soubor o velikosti 50 hodnot jsou na následujícím obrázku. (Data jsou v Datové soubory Tabulka 2.) Vidíme, že odhad s „hladším“ Epanečnikovým jádrem generuje „hladší“ křivku.

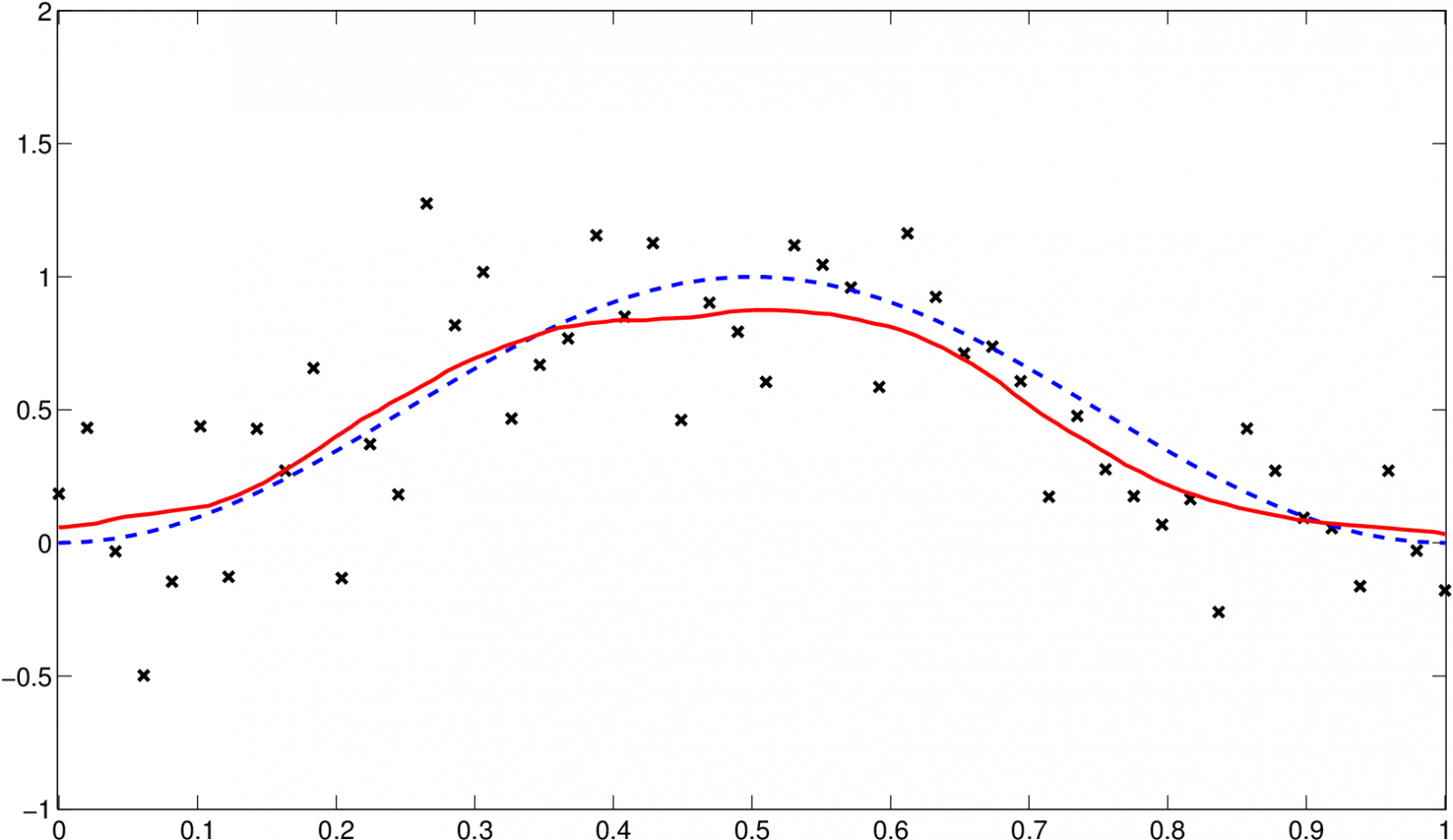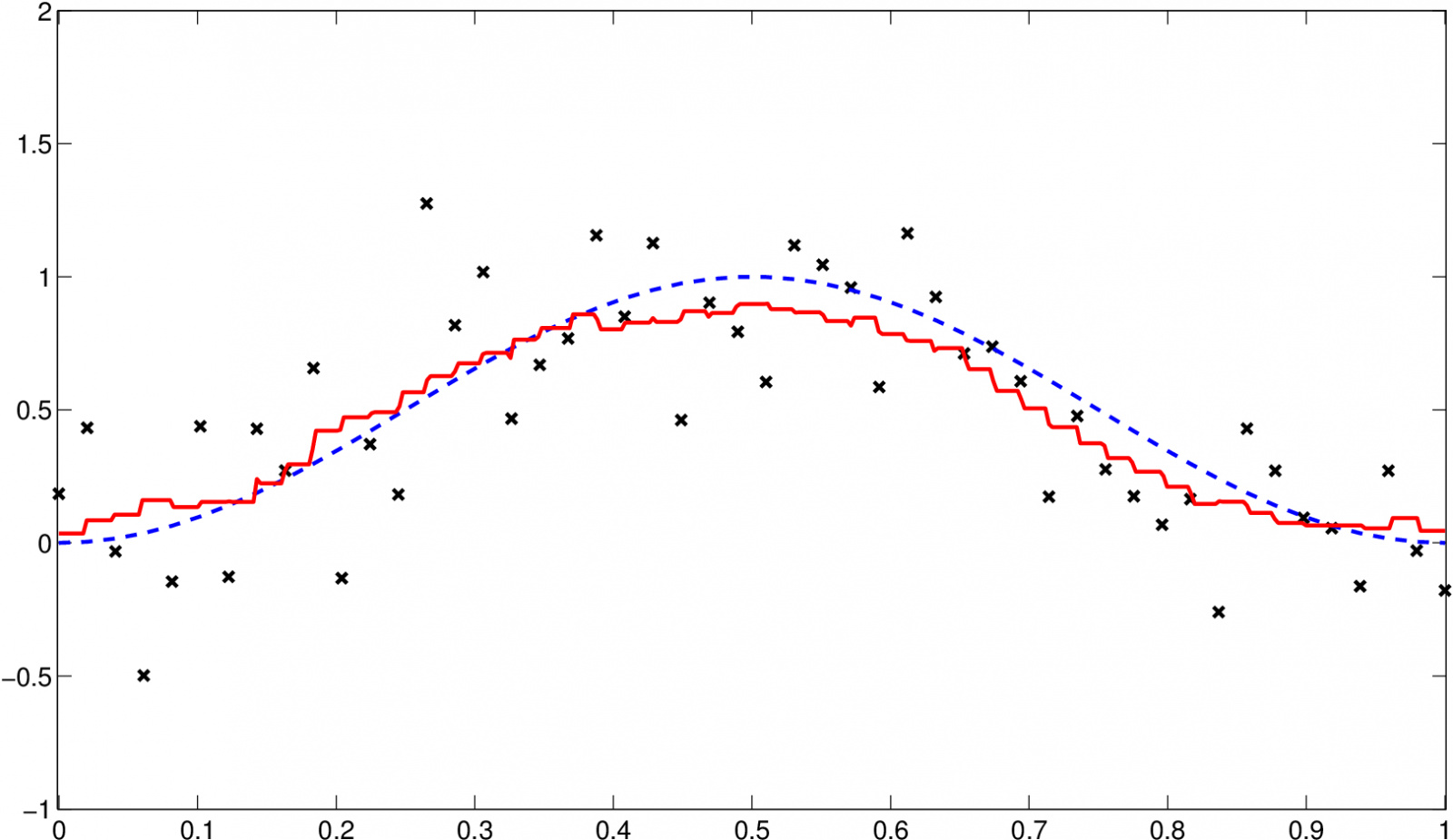a) Epanečnikovo jádro, hopt,0,2=0,1573	b) Obdélníkové jádro, hopt,0,2=0,1236
Obr. 11. Odhad regresní funkce z ukázkového příkladu Jádrové odhady regresní funkce 3.6, odhad (červená, plná) a původní funkce (modrá, čárkovaná)