Základní typy neparametrických odhadů

Nejstarším neparametrickým odhadem hustoty je histogram [12, 13, 14]. Histogram zobrazuje relativní četnosti třídicích intervalů jako plochy obdélníků sestrojených nad těmito intervaly. Pak definujeme odhad hustoty četnosti

kde značí šířku třídicích intervalů (obvykle se volí stejná šířka pro všechny intervaly).

Nevýhody histogramu:

• Histogram je citlivý na počet tříd a jejich šířku.
• Histogram je schodovitá funkce, ale přitom předpokládáme, že neznámá hustota je spojitá.

Příklad 2.1. Mějme dán datový soubor generovaných ze směsi dvou normálních rozdělení a s hustotou

 

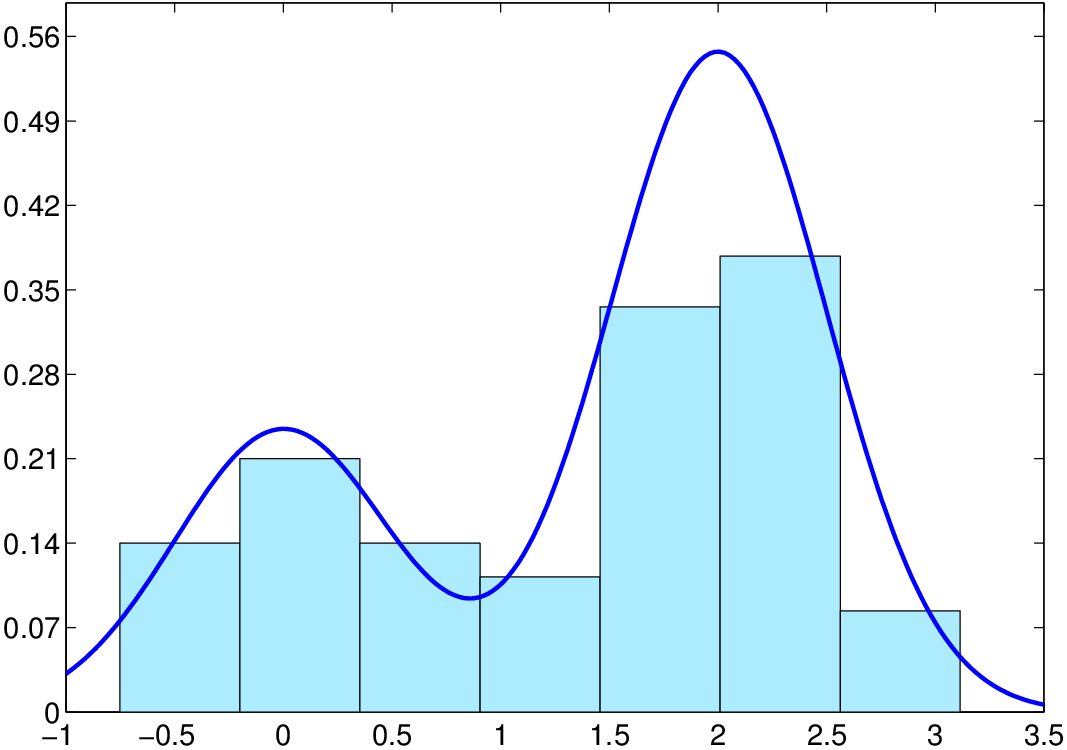
který má rozsah n=100. (Data jsou v Datové soubory Tabulka 3.) Z následujícího obrázku je patrné, že histogram nevystihuje korektně hustotu pravděpodobnosti dat.

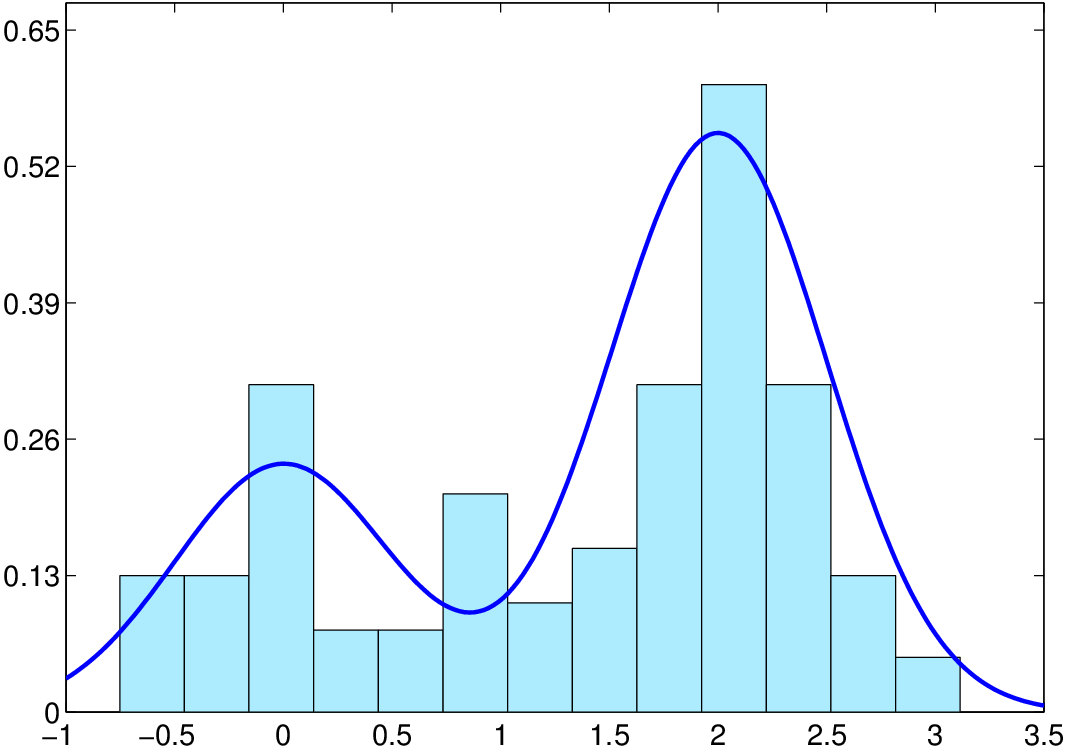
a) 7 intervalů o šířce h=0,55	b) 13 intervalů o šířce h=0,29
Obr. 2. Histogramy s různými počty třídicích intervalů

Výše uvedené problémy lze odstranit použitím jádrových odhadů. Jádrový odhad hustoty v bodě je definovaný vztahem [14] 

(1)

a je vyhlazovací parametr nebo také šířka vyhlazovacího okna.

Jádrový odhad hustoty závisí na třech parametrech: jádře, které hraje roli vahové funkce, vyhlazovacím parametru, který řídí hladkost odhadu, a na řádu jádra, který odpovídá předpokládanému počtu derivací neznámé hustoty.

Popíšeme konstrukci jádrového odhadu:
V každém bodě sestrojíme jádro a odhad v bodě je průměr hodnot jader v tomto bodě. 
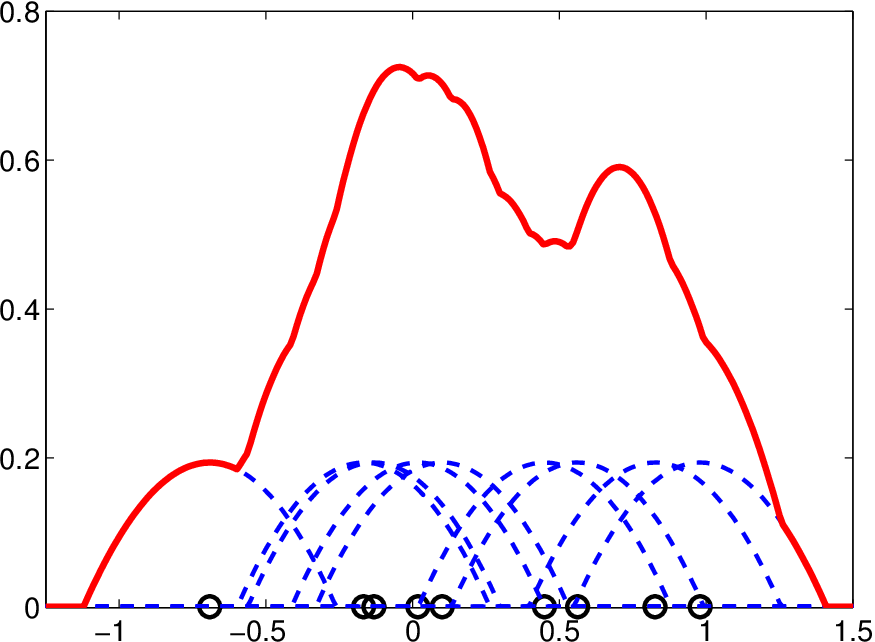
Na obrázku Jádrové odhady hustoty 3a) jsou čárkovaně zobrazena jednotlivá Epančnikova jádra v bodech (kroužky) a plnou čarou je pak zobrazen odhad hustoty.

Otázka. Popište konstrukci odhadu s obdélníkovým jádrem. Jak bude tento odhad vypadat?

Řešení

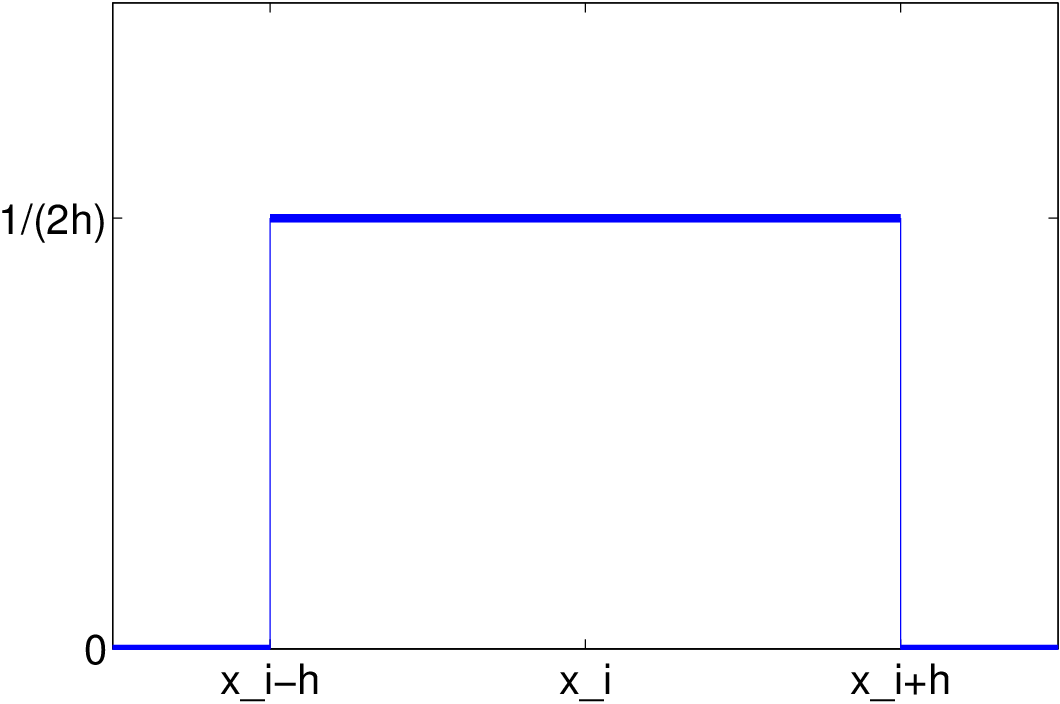
Obdélníkové jádro: pro Odhad hustoty

Tedy v každém bodě sestrojíme obdélník se šířkou a výškou tyto odhady se pak sečtou. Tomuto typu odhadu se také říká naivní odhad. Naivní odhad v jistém smyslu osvobozuje histogram od volby polohy třídicích intervalů. Tento odhad „klouže“ přes data  - jako histogram pro odhad hustoty odpovídá regresogramu pro odhad regresní funkce, tak výsledek odhadu hustoty s obdélníkovým jádem odpovídá klouzavému průměru u regrese.

Nyní uvedeme ještě vztah pro jádrový odhad -té derivace hustoty. Budeme předpokládat, že  a jsou stejné parity. Pak

(2)

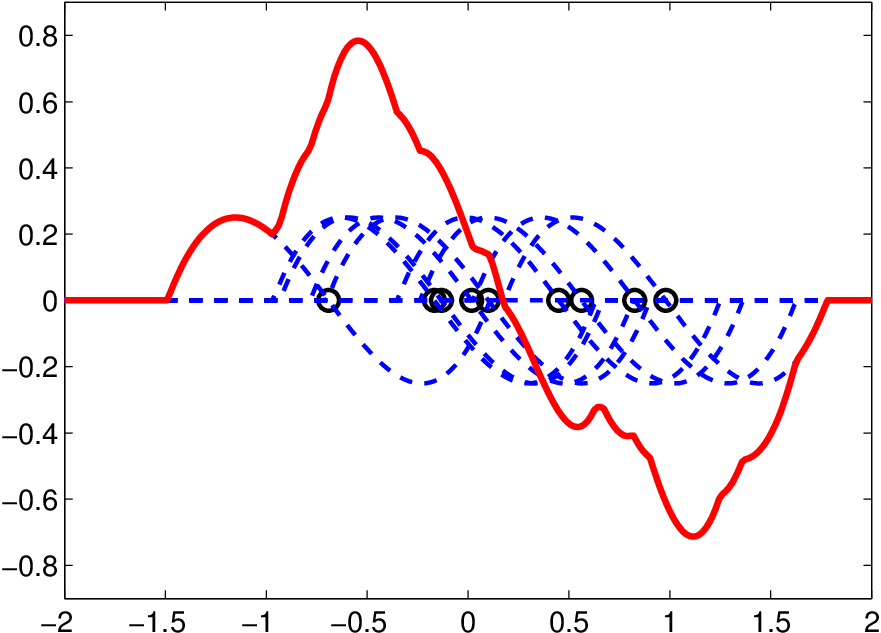
Konstrukce jádrového odhadu derivace je stejná jako konstrukce odhadu hustoty. V každém bodě sestrojíme jádro ze třídy ¹ a odhad v bodě je průměrem hodnot jader v tomto bodě. Na obrázku Jádrové odhady hustoty 3b) je zobrazen odhad první derivace hustoty pro soubor o devíti pozorování a bylo zde použito jádro

a) Odhad hustoty s Epančnikovým jádrem	b) Odhad derivace hustoty s jádrem Kopt  S13
Obr. 3. Konstrukce jádrového odhadu hustoty a její derivace

¹Jádra viz tabulku Jádrové funkce a jejich vlastnosti 1