Motivace

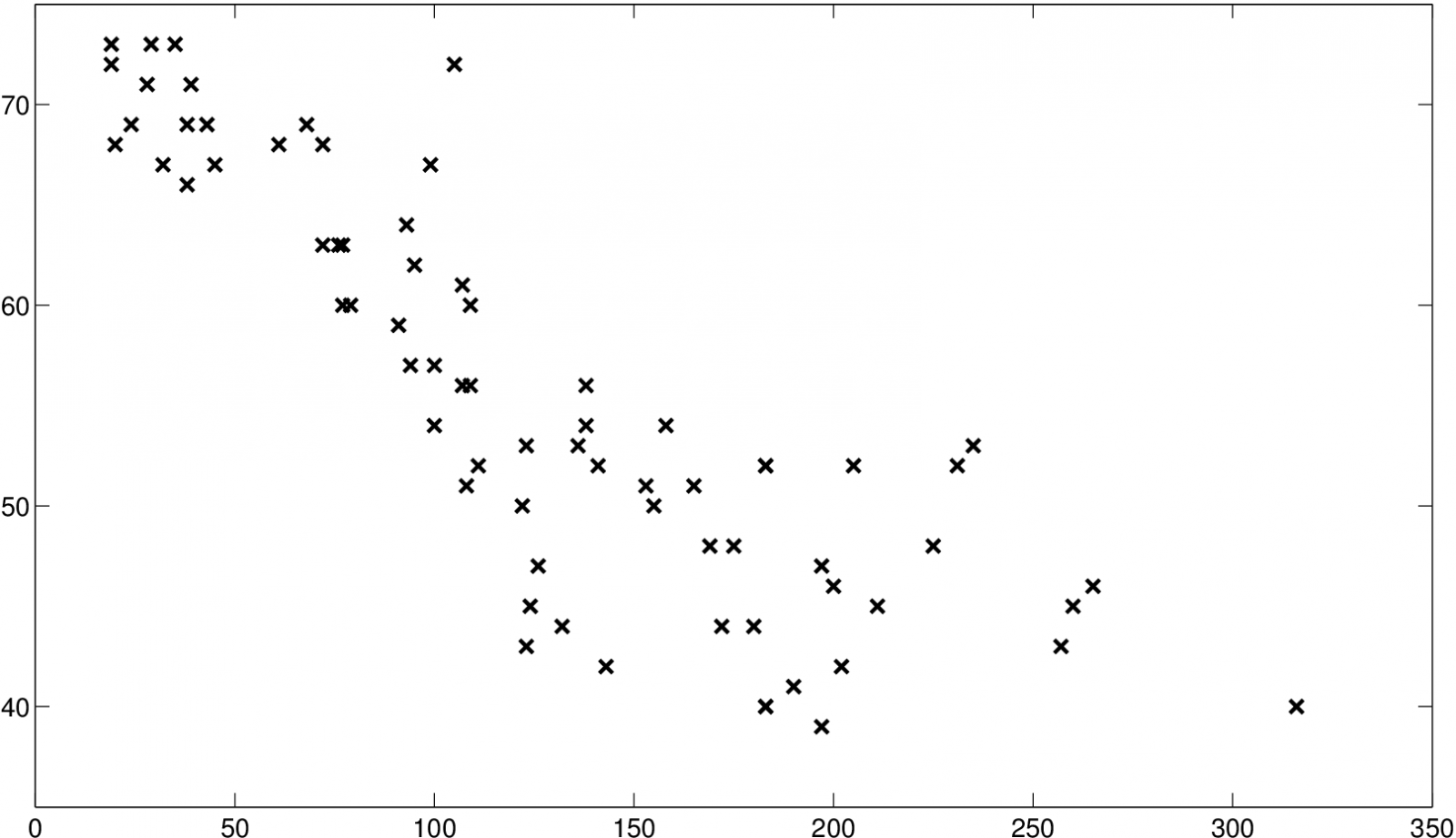
Uvažujme soubor dat ze studie The State of the World's Children (UNICEF), který obsahuje míru úmrtnosti dětí od narození do pěti let věku počítanou na 1000 živě narozených dětí a očekávanou délku života narozeného dítěte (s ohledem na úmrtnost v dané populaci v době jeho narození) v 72 zemích, které měly v roce 2001 hrubý národní produkt menší než 1000 amerických dolarů na osobu a rok.

Obr. 1. Studie UNICEF - míra úmrtnosti (osa x) a očekávaná délka života u dětí (osa y)

Chceme vědět, jaká je pravděpodobnost, že dítě narozené v zemi s vysokou mírou úmrtnosti, se dožije vyššího věku. Případně, zda se v datech nevyskytují shluky, tj. zda jde o vícemodální hustotu. V tomto případě se jedná o odhad dvourozměrné hustoty.

Odhady vícerozměrných hustot se budeme zabývat v této kapitole. Ovšem ve vícerozměrném případě nevystačíme s jedním vyhlazovacím parametrem, ale je třeba specifikovat matici vyhlazovacích parametrů. Tato matice řídí jak hladkost, tak i orientaci vícerozměrného vyhlazení. Budeme se zabývat jádrovým odhadem, který je přímým rozšířením jednorozměrného odhadu Jádrové odhady regresní funkce (1), a zaměříme se zejména na odhad dvourozměrné hustoty. Tedy naším cílem je rekonstruovat hustotu pravděpodobnosti z náhodného výběru.

Poznámka 1.1. Jádrové odhady dvourozměrných hustot se obvykle znázorňují pomocí vrstevnic, které umožňují snazší náhled na odhadnutou funkci.