Metoda referenční hustoty

Nejčastěji se pro odhad neznámé veličiny (viz rovnice Jádrové odhady hustoty (3)) používá parametrické třídy hustot. Jednou z možností je použít standardní normální hustotu s rozptylem tj. předpokládáme, že

V tomto případě je odhad optimálního vyhlazovacího parametru tvaru pro

(12)

Je třeba ještě odhadnout směrodatnou odchylku To lze dvěma způsoby:

		(13)
		(14)

kde je standardní normální kvantilová funkce a číslo respektive je horní, respektive dolní výběrový kvartil. Je vhodné volit

Poznámka 5.2. Pokud za jádro zvolíme Gaussovo jádro (k=2)

pak dostaneme jednoduchý vztah [11, 12]

(15)

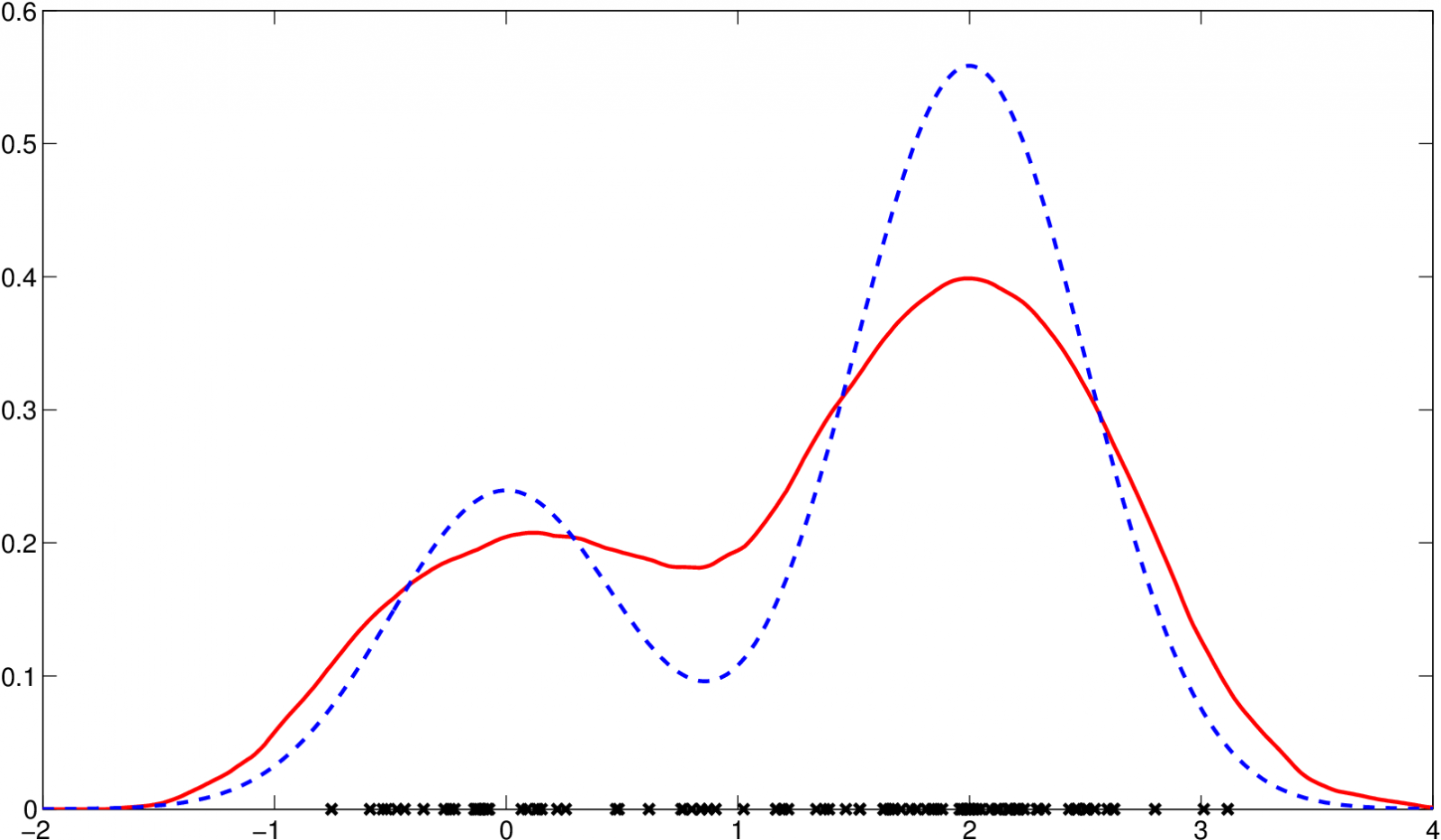
Příklad 5.3. Použijme odhad vyhlazovacího parametru pro data z příkladu Jádrové odhady hustoty 2.1 metodou referenční hustoty. Pro Epanečnikovo jádro, které je řádu k=2, se vztah Jádrové odhady hustoty (12) zjednoduší na tvar

Dále odhadneme směrodatnou odchylku: tedy Po dosazení počtu prvků a parametru získáme hodnotu vyhlazovacího parametru pro odhad hustoty Na následujícím obrázku je vykreslen odhad hustoty s tímto parametrem.

Obr. 7. Odhad hustoty s hREF =0,9639$, odhad (červená,  plná), původní funkce (modrá, čárkovaná)

Otázka. Jak hodnotu bude mít odhad vyhlazovacího parametru pomocí metody referenční hustoty pro hustotu z ukázkového příkladu Jádrové odhady hustoty 3.5?