
Metoda křížového ověřování
Jednou z nejrozšířenějších a nejpoužívanějších metod pro určení optimální hodnoty parametru je metoda křížového ověřování (cross-validation method). Tato metoda je založena na odhadu regresní funkce Jádrové odhady regresní funkce (4), v němž vynecháme
-té pozorování:
Funkce křížového ověřování je definována takto
|
|
(14) |
a odhadem optimální hodnoty vyhlazovacího parametru je bod, v němž nastává minimum této funkce, tj.
Hledáme tedy minimum na intervalu jehož tvar plyne ze vztahu Jádrové odhady regresní funkce (13), přičemž
jsou konstanty
které ovšem neznáme. A proto pro ekvidistantní body plánu byl na základě zkušeností doporučen interval
Poznámka 5.1. Někdy se místo chyby používá průměrná střední kvadratická chyba
(average mean square error)
Využívá se zejména v případech, kdy není vhodné použít numerické integrování související s chybou, která se vyskytuje v .
Věta 5.2. Pro střední hodnotu funkce platí
Důkaz. Funkci křížového ověřování lze rozepsat
|
|
|
|
Střední hodnota je rovna součtu tří veličin. Předpokládejme, že
pak první ze sčítanců je roven přímo
Dále víme, že a tedy pro druhý sčítanec platí:
Stejně jako pro druhý sčítanec, i pro třetí sčítanec využijeme vlastnosti Jádrové odhady regresní funkce (2):
Tento výsledek znamená, že minimalizace odpovídá minimalizaci
Jestliže tedy předpokládáme, že minimum
je blízko minima
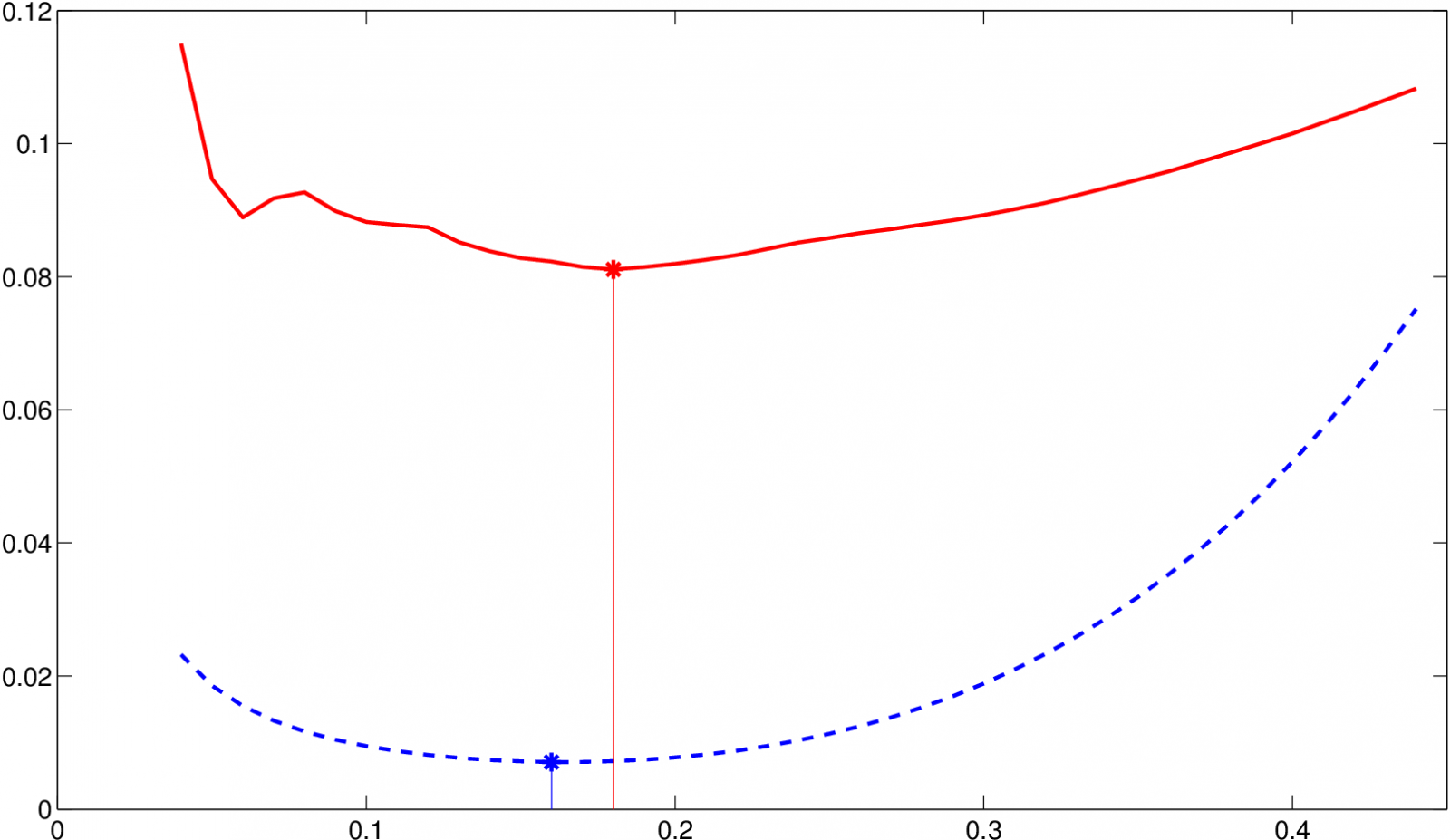
pak tato minimalizace dává dobrou volbu vyhlazovacího parametru - viz ilustrace na následujícím obrázku.
 |
|
Obr. 12. Porovnání minima AMSE (modrá, čárkovaná) a minima funkce křížového ověřování CV (červená, plná) pro simulovaná data z ukázkového příkladu
|
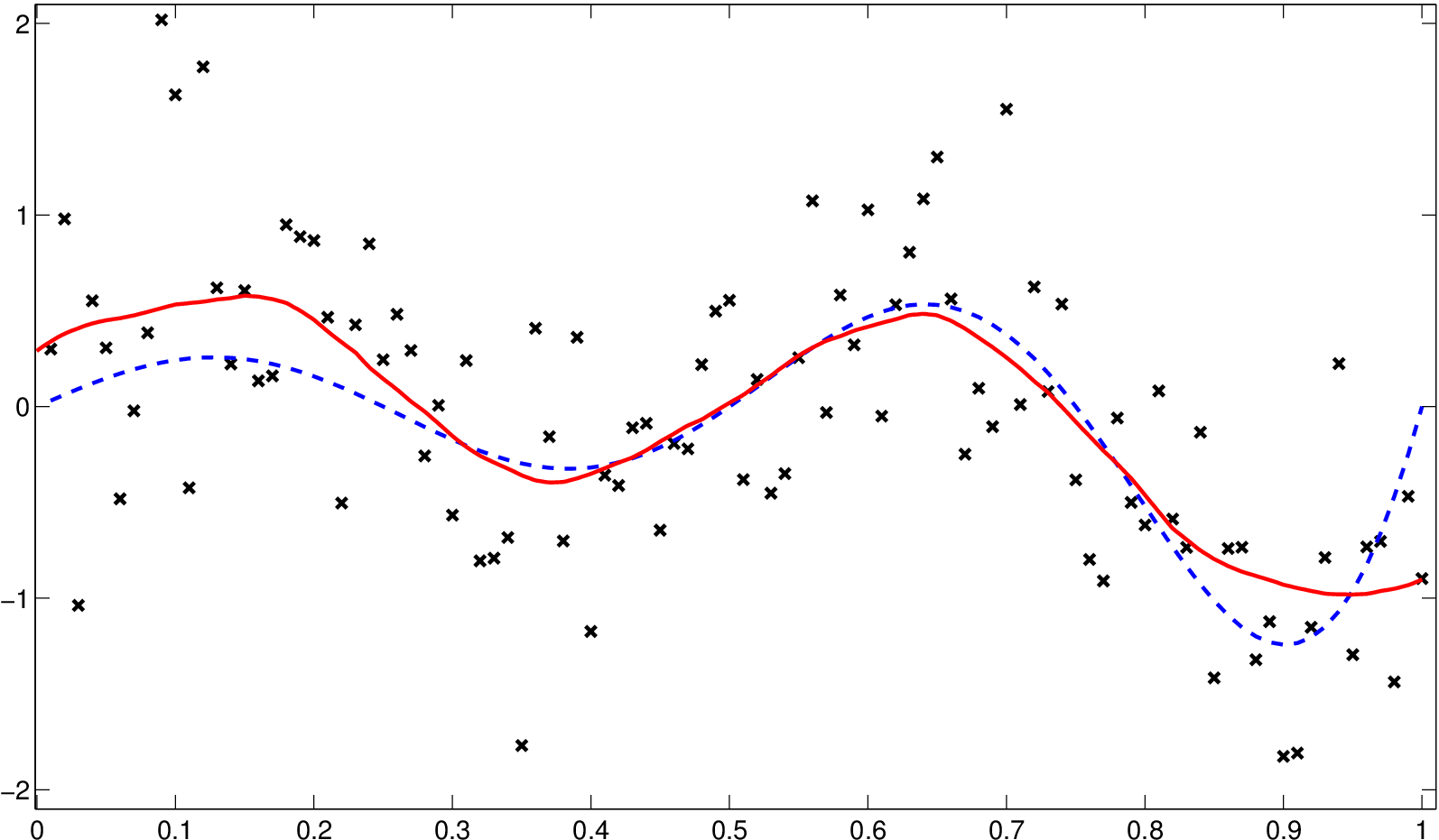
Příklad 5.3. Použijeme metodu křížového ověřování pro nalezení vyhlazovacího parametru pro data z příkladu Jádrové odhady regresní funkce 1.2. Při použití Epanečnikova jádra získáme vyhlazovací parametr Na následujícím obrázku je zobrazen odhad regresní funkce s tímto parametrem.
 |
|
Obr. 13. Simulovaná data (x) s jádrovým odhadem regresní funkce (hCV =0,1158) (červená, plná) a původní funkcí (modrá, čárkovaná)
|
Kromě metody křížového ověřování se také pro odhad optimálního vyhlazovacího parametru používají metody založené na (average square error), metody plug-in, metody odvozené z Fourierovy transformace a bootstrapové metody (podrobněji např. [3, 6]).




