Princip maximálního vyhlazení

Myšlenka této metody je stejná jako pro odhad hustoty. Užijeme-li faktu, že

můžeme aplikovat Terrelovu větu pro V tomto případě je

a tedy

kde . Odtud plyne, že

(9)

je odhadem (viz rovnice Jádrové odhady hustoty (13) a Jádrové odhady hustoty (14)).

Poznámka 5.1. Hodnota může sloužit jako horní hranice pro množinu vyhlazovacích parametrů volených podle metody křížového ověřování. Tedy kde je nejmenší vzdálenost mezi po sobě jdoucími body

Příklad 5.2. Pro data z příkladu Jádrové odhady distribuční funkce 2.1 zvolme Epanečnikovo jádro. Pak hodnoty potřebné pro odhad vyhlazovacího parametru metodou maximálního vyhlazení jsou následující:

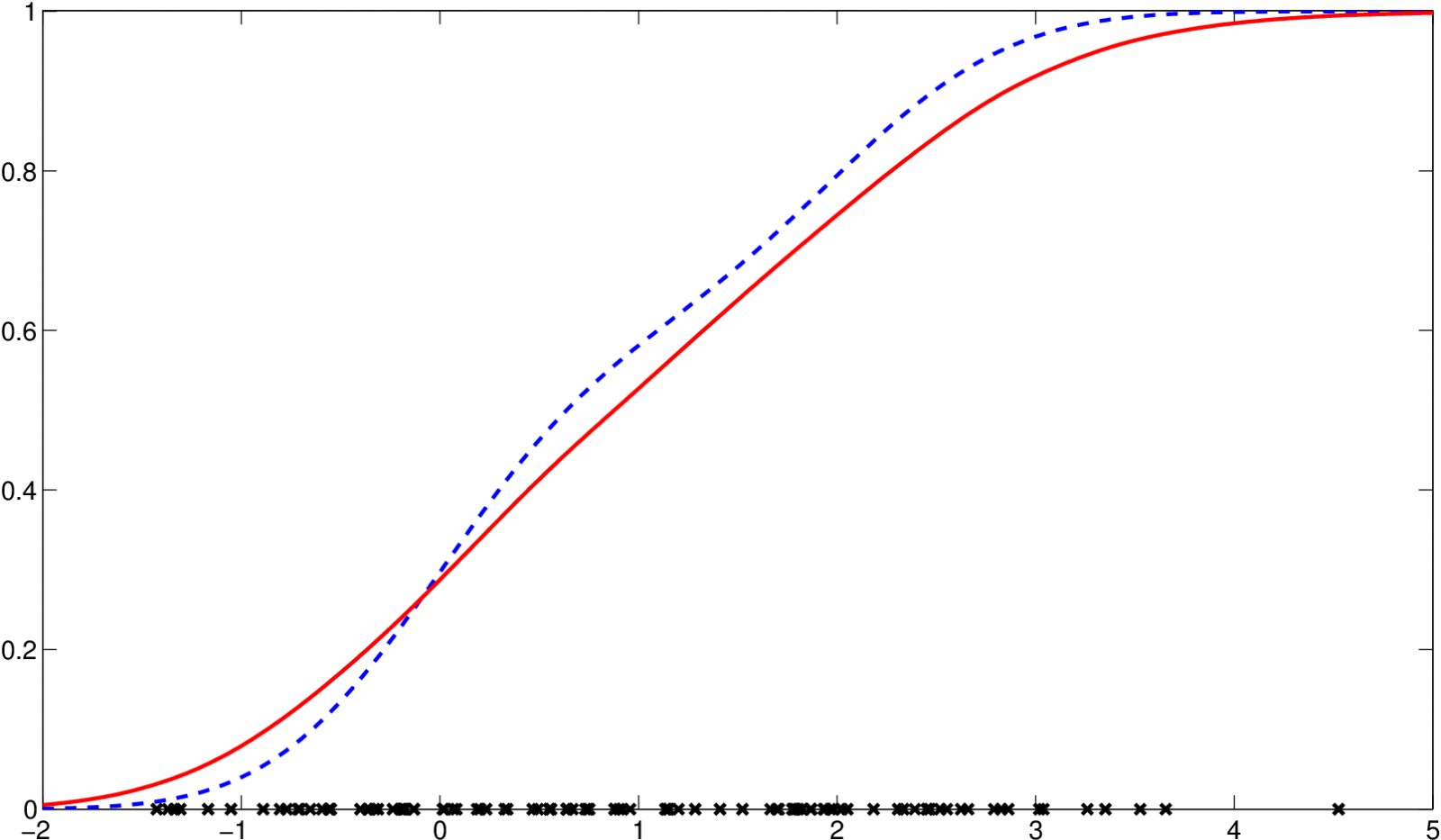
Pak platí a na následujícím obrázku je zobrazen odhad distribuční funkce.

Obr. 6. Odhad distribuční funkce s hMS =1,1037$, odhad (červená, plná), původní funkce (modrá, čárkovaná)