Statistické vlastnosti jádrových odhadů hustoty

Stejně jako u jádrových odhadů regresní funkce lze kvalitu jádrového odhadu hustoty popsat lokálně pomocí střední kvadratické chyby.

Věta 3.1. Střední kvadratická chyba je tvaru

Důkaz. Spočítejme střední hodnotu odhadu

Vychýlení pak bude mít tvar

Dále upravíme vztah pro rozptyl

Důsledek. Střední integrální kvadratická chyba nabývá tvaru

Podobně jako u odhadu regresní funkce můžeme použít globální pohled na kvalitu odhadu, a to pomocí střední integrální kvadratické chyby a jejího asymptotického tvaru

Věta 3.2. Nechť funkce má spojité derivace až do řádu (tj. ) pro a dále předpokládejme a pro Pak platí

kde

Důkaz. Nejprve vypočteme střední hodnotu

dále použijeme Taylorův rozvoj:

Tedy vychýlení odhadu je tvaru

a tedy

Nyní dokážeme vztah pro rozptyl. Víme, že

a dále počítáme

Tedy

a pak využijeme faktu, že

Důsledek. Nechť pro pak je konzistentním odhadem tj. a

Stejně jako u odhadu regresní funkce má význam asymptotická integrální střední kvadratická chyba

kde je tvaru

(3)

V dalších částech textu budeme využívat označení jednotlivých částí chyby , která je součtem asymptotického tvaru integrálu rozptylu (asymptotic integrated variance) a asymptotického tvaru integrálu druhé mocniny vychýlení (asymptotic integrated squared bias):

tedy

Užitím vztahů a pro lze zapsat ve tvaru

(4)

Důkaz viz Cvičení 1.

Odtud je zřejmé, že vyhlazovací parametr, pro nějž nabývá minimální hodnoty, je dán vztahem

(5)

tj.

Vypočtěme hodnotu při dosazení optimálního parametru

(6)

tj.

I v tomto případě, podobně jako u odhadhu regresní funkce, platí vztah mezi asymptotickým rozptylem a vychýlením

(7)

Nyní uvedeme zajímavou vlastnost vyhlazovacího parametru.

Poznámka 3.3. Nechť Pak optimální hodnota vyhlazovacího parametru je

Počítejme derivace dané rovnicí Jádrové odhady hustoty (3) pro k=2

Řešením rovnice je

tj. také realizuje minimum

Lze ukázat, že

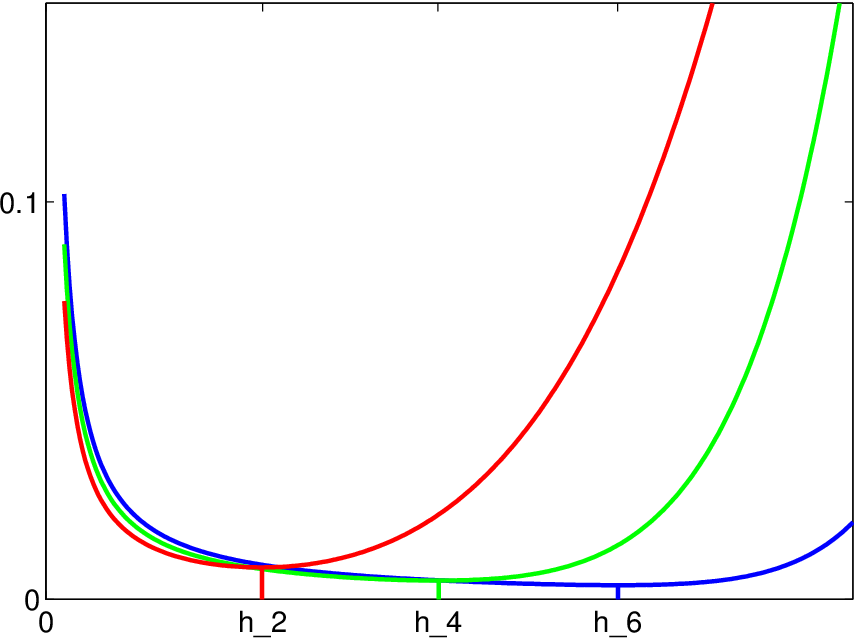
a to znamená, že pro jádra vyšších řádů je minimum plošší a tedy volba blízká optimální hodnotě nevede k velkému růstu . Na následujícím obrázku jsou zobrazeny body minima funkce pro hustotu normálního rozdělení se sto prvky.

Obr. 4. pro jádra vyšších řádů s vyznačenými minimálními hodnotami pro jádra řádu 2,4,6$

Vztah pro optimální hodnotu vyhlazovacího parametru poskytuje informaci, že asymptoticky je Ale vztah má pouze teoretický charakter, protože optimální parametr závisí na neznámé hustotě Je zde tedy opět problém s volbou tohoto parametru. Metodám pro odhad vyhlazovacího parametru je věnován odstavec Volba vyhlazovacího parametru.

Poznámka 3.4. Z předchozích úvah je zřejmé, že množina přípustných hodnot vyhlazovacích parametrů je dána vztahem

kde jsou konstanty,

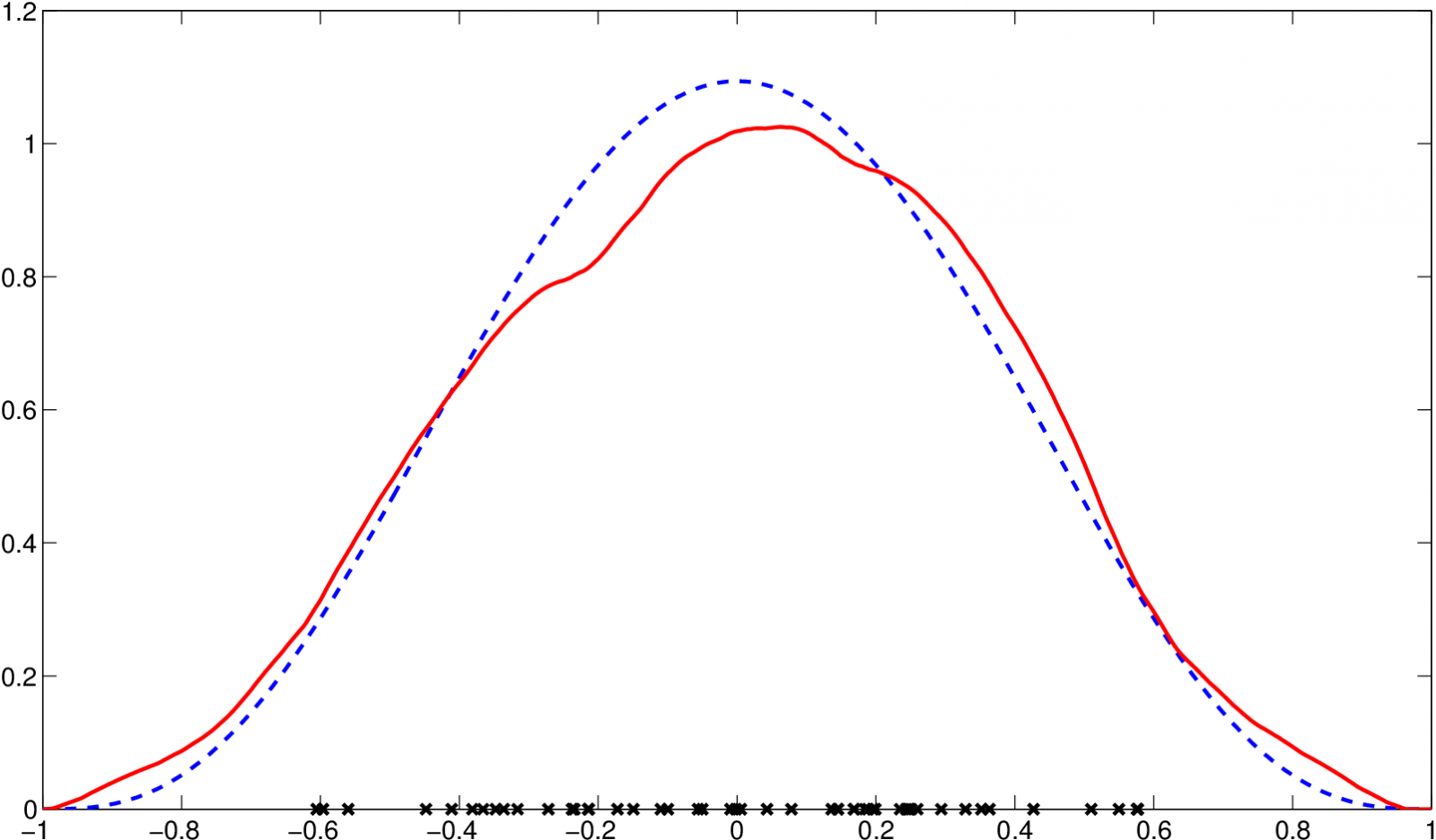
Příklad 3.5. Máme k dispozici data, která pocházejí z rozdělení s hustotou pro Vypočítejme hodnotu optimálního vyhlazovacího parametru pro odhad s jádrem řádu 2.

Podle vztahu Jádrové odhady hustoty (5) potřebujeme spočítat výraz

Výpočet pro Epanečnikovo jádro: tedy

Tedy pro soubor 50 hodnot bude Odhad s optimálním vyhlazovacím parametrem pro tento datový soubor (viz tabulku Datové soubory Tabulka 4) je na následujícím obrázku.

Obr. 5. Odhad hustoty z příkladu, odhad (červená, plná) a původní funkce (modrá, čárkovaná) při použití Epanečnikova jádra a hopt,0,2=0,3860$