Základní typy neparametrických odhadů

Nechť jsou nezávislé náhodné proměnné, které mají tutéž spojitou hustotu a distribuční funkci Nejjednodušší neparametrický dohad distribuční funkce je empirická distribuční funkce definovaná v bodě vztahem

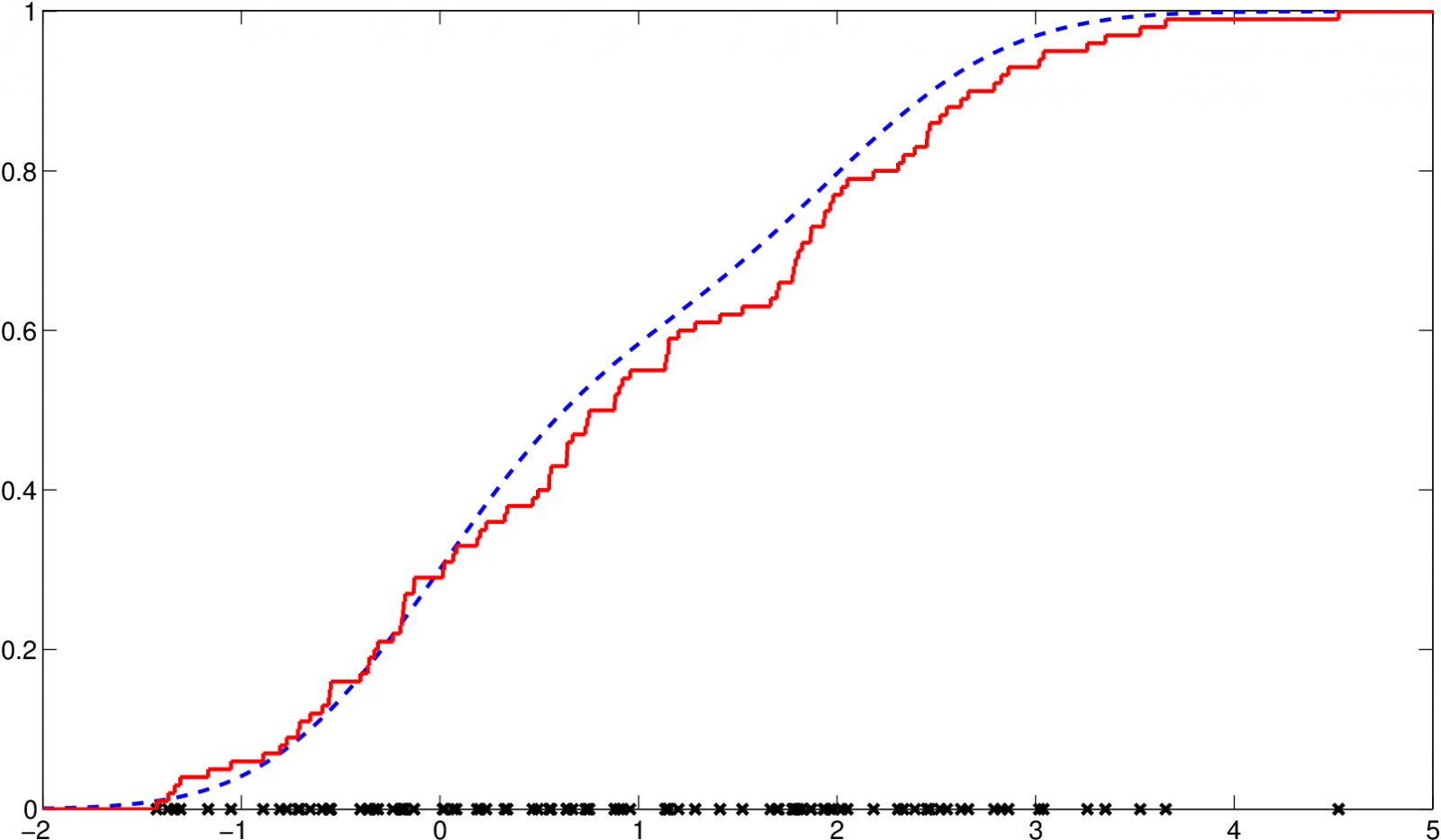
Tento odhad má sice dobré statistické vlastnosti, ale je to schodovitá funkce (viz obr. Jádrové odhady distribuční funkce 2), a proto se budeme zabývat postupy, které umožní zkonstruovat „hladký“ odhad distribuční funkce

Příklad 2.1. Mějme dán náhodný výběr o velikosti n=100 ze směsi dvou normálních hustot a s hustotou (viz kapitola Jádrové odhady hustoty) (Data jsou v tabulce Datové soubory Tabulka 5.)

Z nasledujícího obrázku je patrné, že schodovitá funkce nevystihuje plně charakter distribuční funkce.

Obr. 2. Empirická distribuční funkce Fn (červená, plná) a skutečná distribuční funkce F (modrá, čárkovaná) pro data z příkladu Jádrové odhady distribuční funkce 2.1

Nejznámější postup, jak odvodit neparametrický odhad distribuční funkce, spočívá v integraci jádrového odhadu hustoty, t.j.

Užijeme-li substituce dostaneme

To znamená, že odhad v bodě je definován takto

(1)

Zde předpokládáme, že pro Níže jsou uvedeny základní vlastnosti funkce

1.	pro a pro
2.
3.
4.

Otázka. Lze použít obdélníkové jádro? Jaký bude tvar a vlastnosti funkce

Řešení

Obddélníkové jádro tedy funkce

Vlastnosti

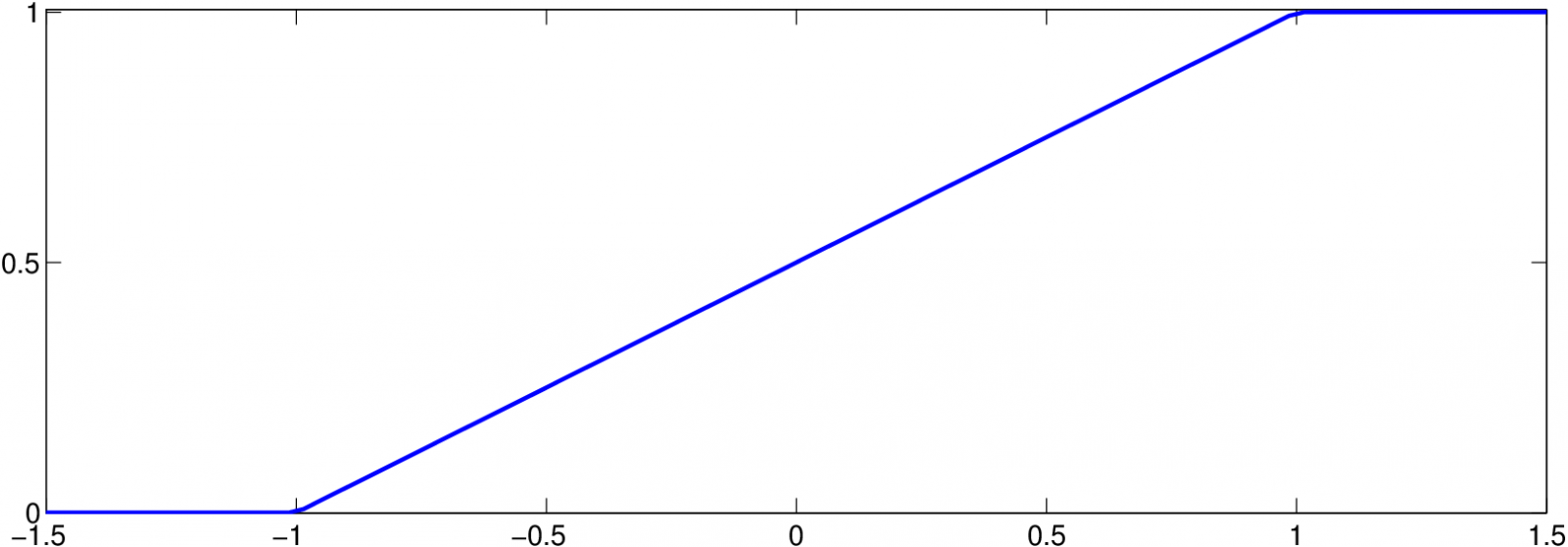
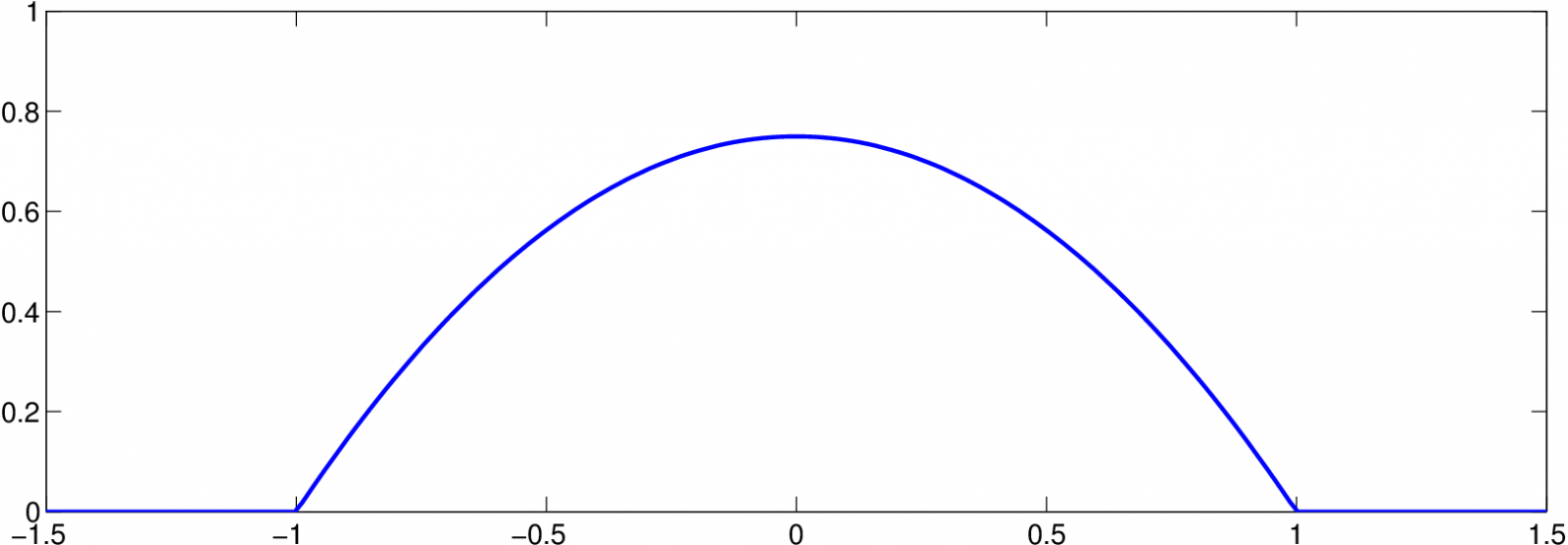
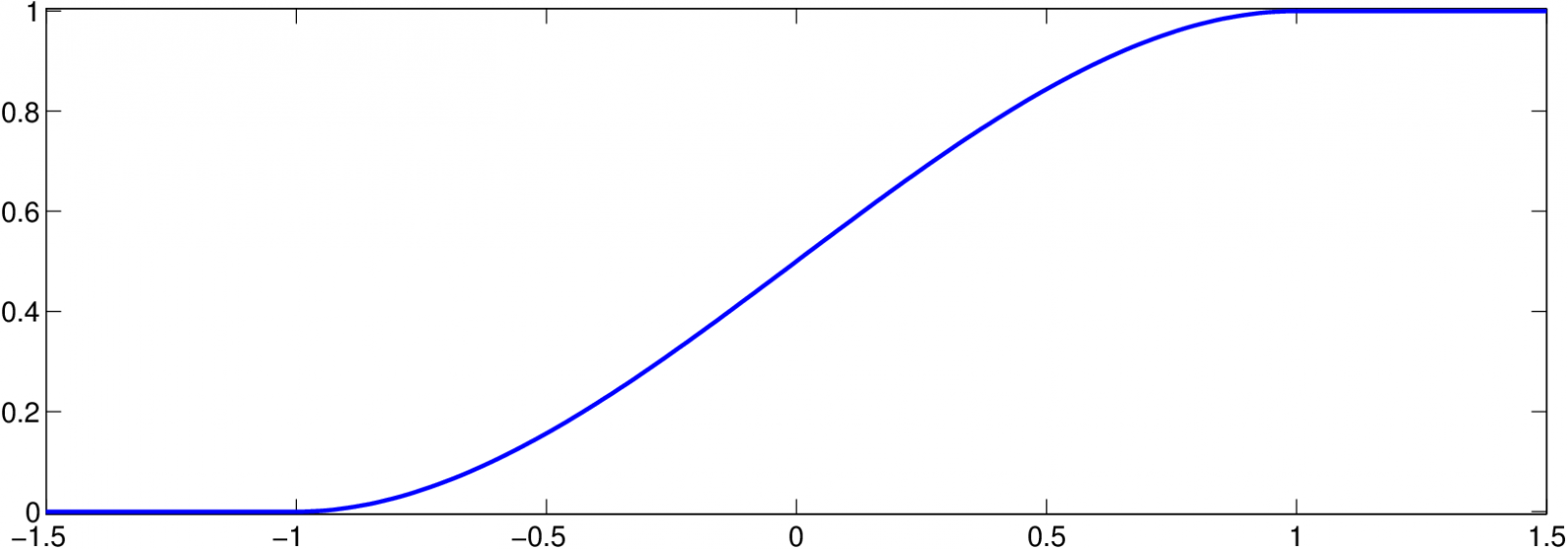
Příklad 2.2. Použijeme-li Epanečnikovo jádro pak funkce je tvaru

Obr. 3. Epanečnikovo jádro K (vlevo) a k němu příslušná funkce W (vpravo)

 

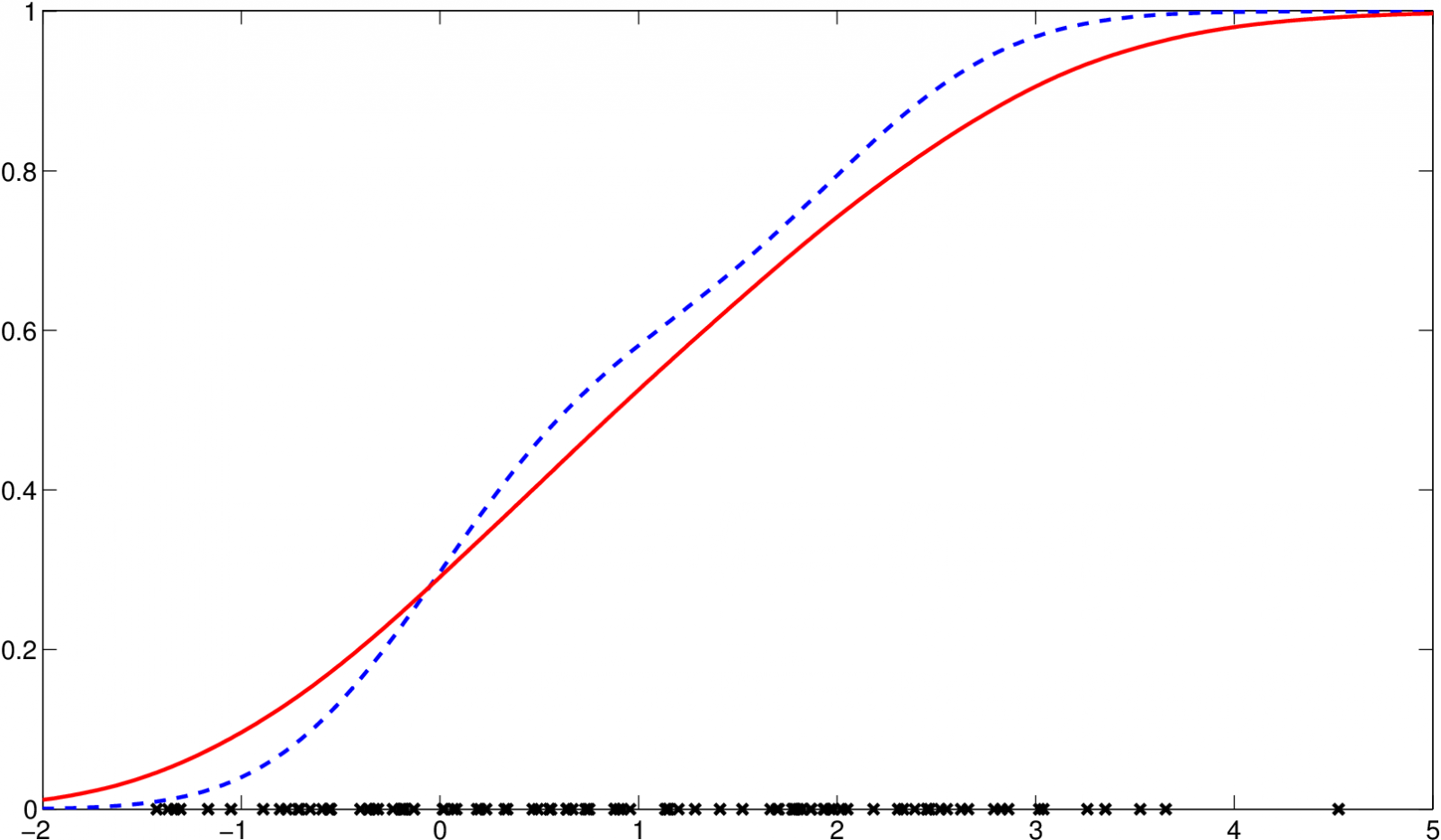
Pro data z příkladu Jádrové odhady distribuční funkce 2.1 je jádrový odhad distribuční funkce prezentován na následujícím obrázku.

Obr. 4. Jádrový odhad distribuční funkce s parametrem h=1,5, odhad (červená, plná), původní funkce (modrá, čárkovaná)