Aplikace na reálná data

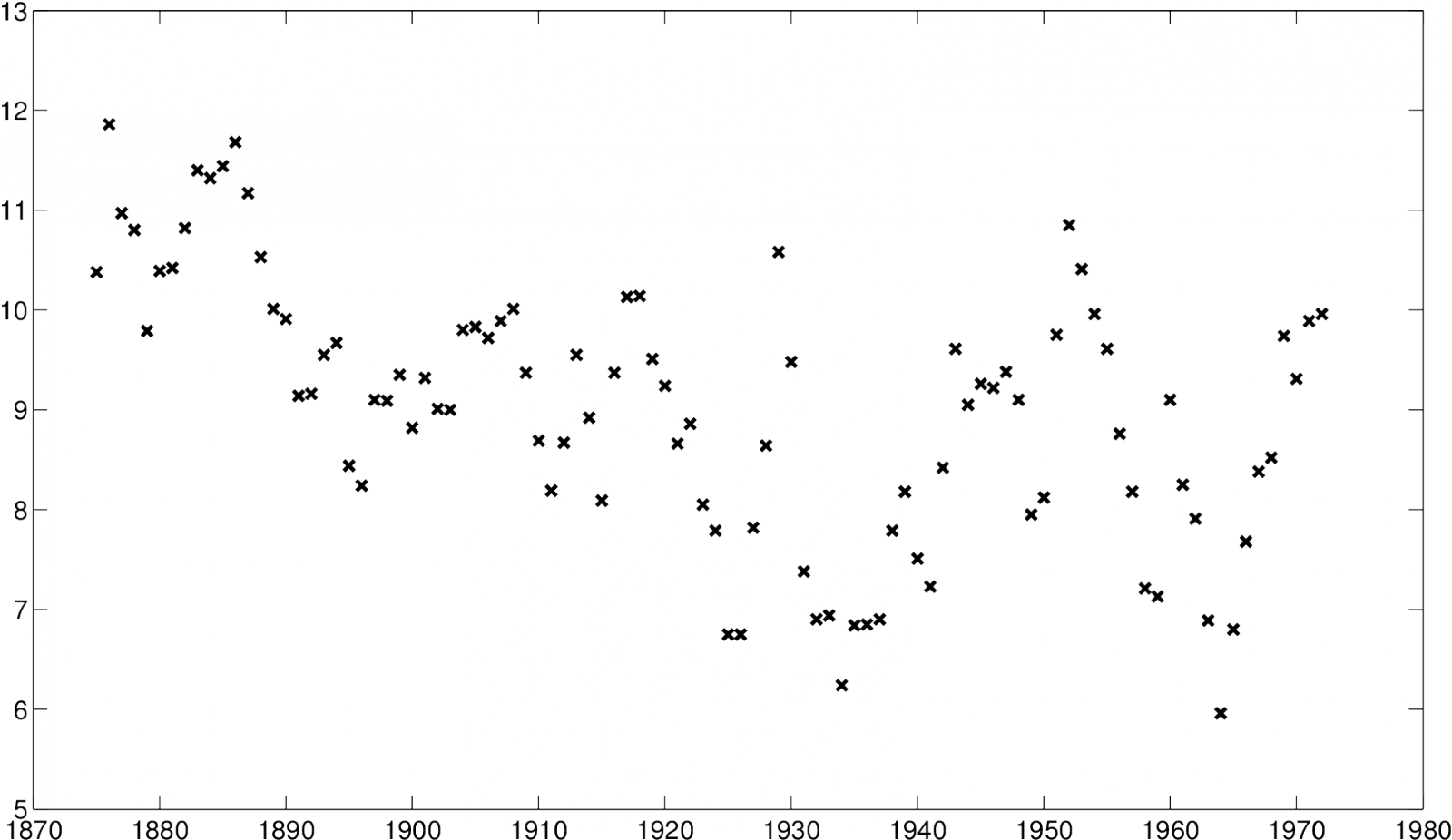
Nyní se vrátíme k motivačnímu příkladu. Datový soubor obsahuje měření úrovně hladiny vody v Huronském jezeře. Měření byla prováděna ročně, v letech 1875 až 1972, tedy naměřené hodnoty jsou ekvidistantní. Data jsou shrnuta v Datové soubory Tabulka 8 a na obrázku Jádrové odhady regresní funkce 15a).

Vyhlazovací parametry jsme odhadli pomocí metody křížového ověřování (za použití Epanečnikova jádra) a také pomocí automatické procedury. Hodnoty vyhlazovacích parametrů jsou následující:

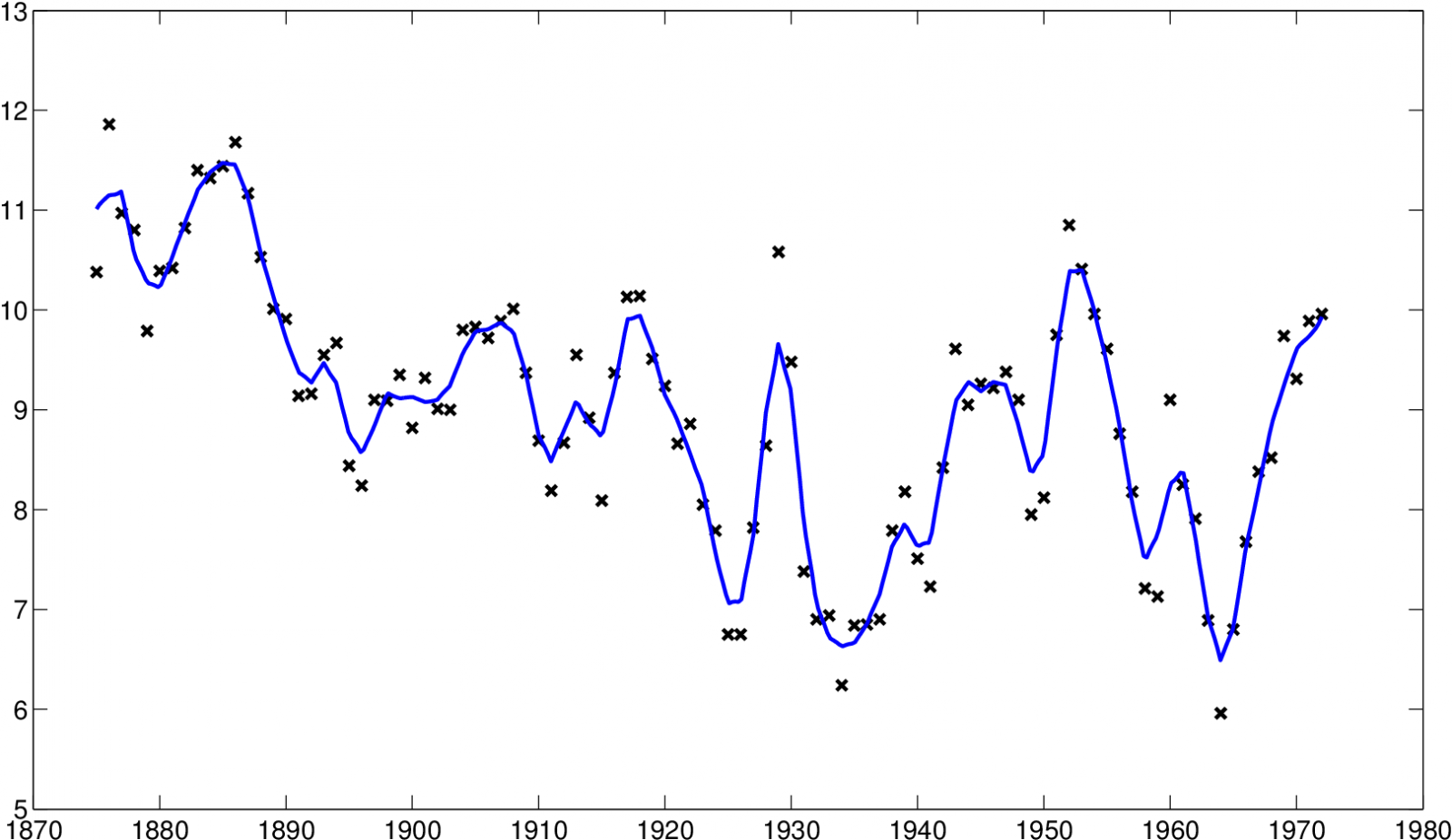
Výsledná křivka je odhadem funkce popisující průběh úrovně hladiny v letech 1875 až 1972. Odhady na následujícím obrázku ukazují, že metoda křížového ověřování spíše podhlazuje.

a) Data
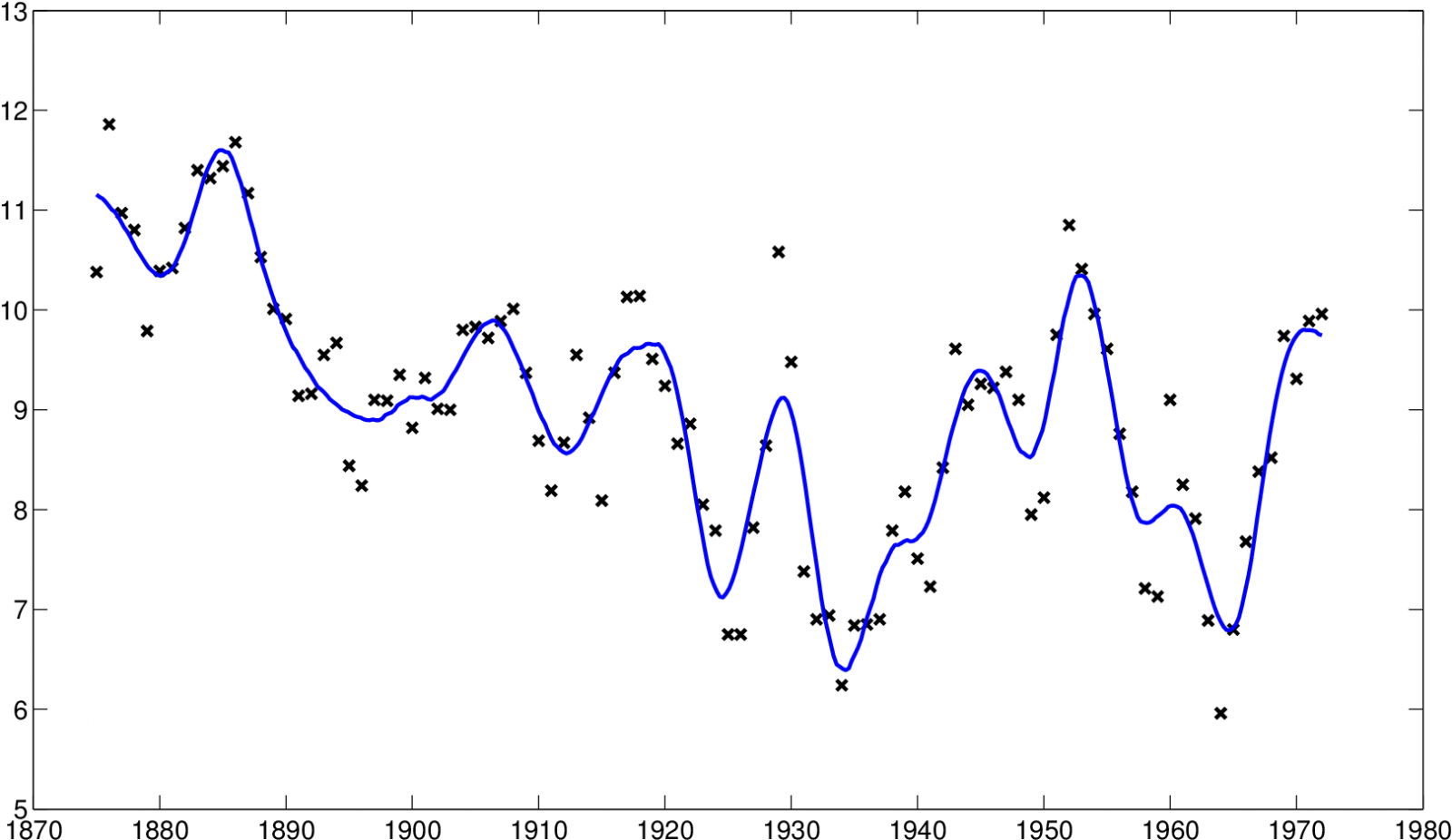
b) hCV=0,0204, Kopt,0,2	c) hCV=0,1525, Kopt,0,12
Obr. 15. Úroveň hladiny Huronského jezera - data a odhadnuté regresní funkce, na ose x jsou roky a na ose y je hladina vody ve stopách (snížená o 570 stop - viz poznámka u dat Datové soubory Tabulka 8)

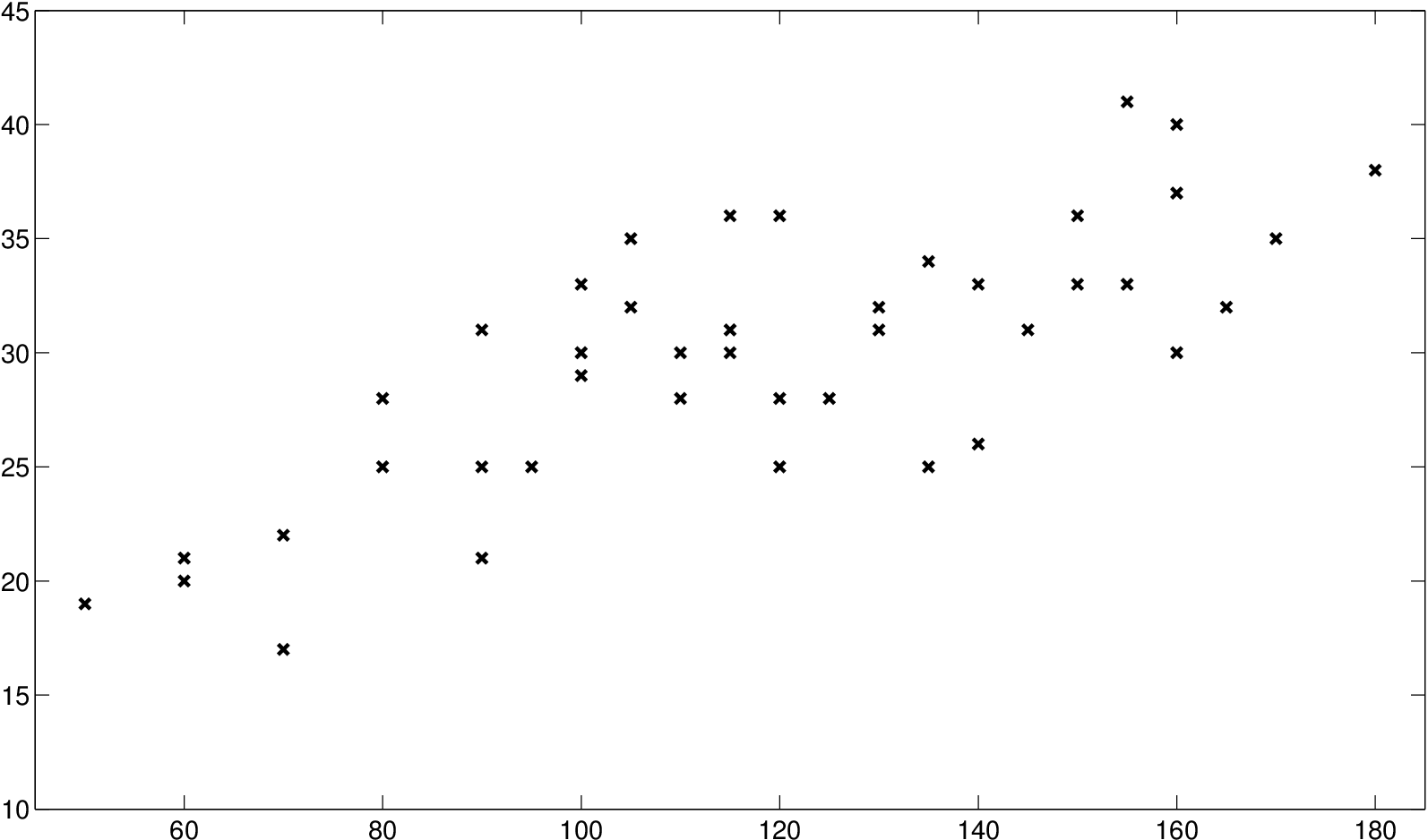
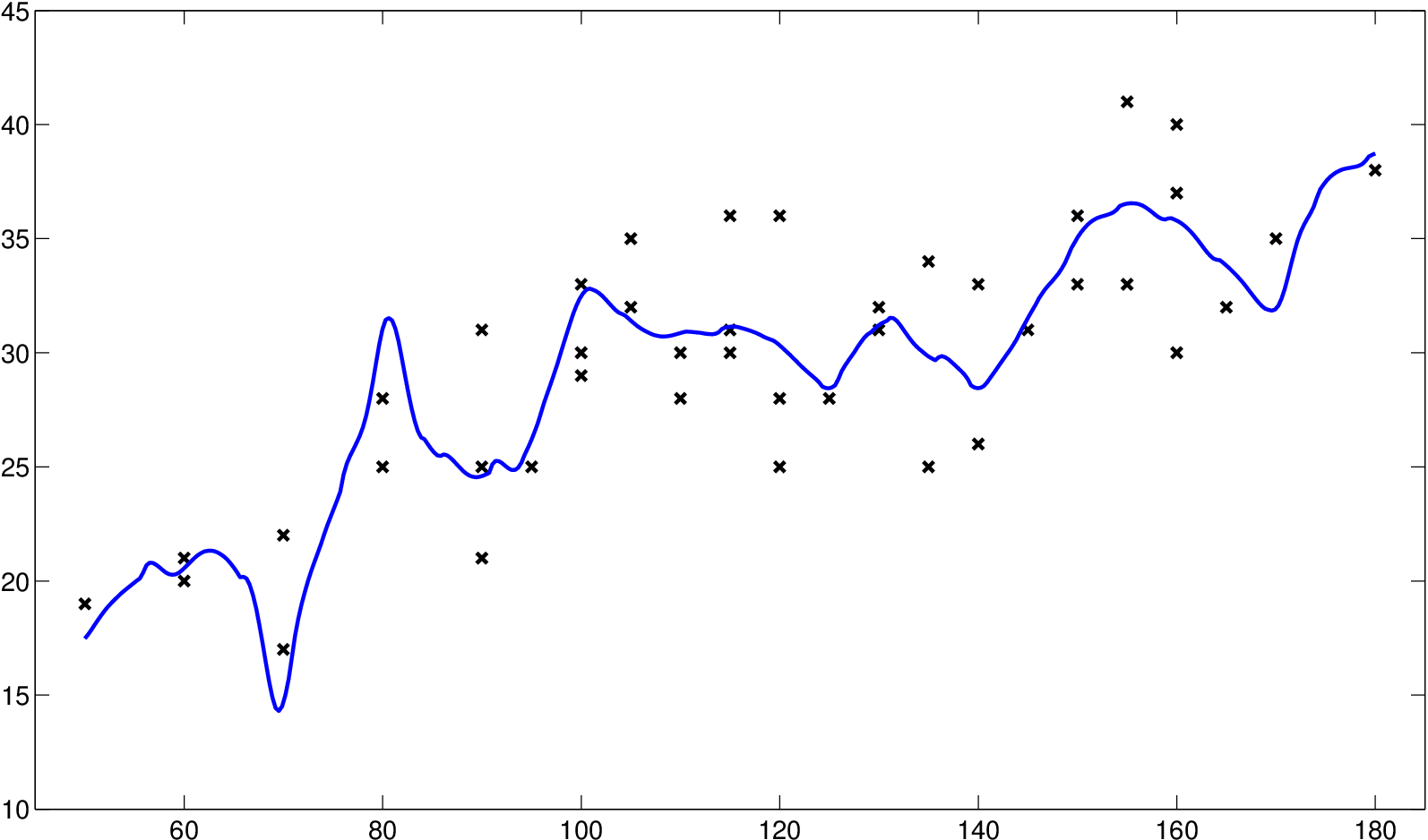
Druhým datovým souborem jsou měření axiální délky krystalů ledu. Měření byla prováděna v místnosti s konstantní teplotou -5°C v časových intervalech 50 až 180 vteřin po přinesení krystalu do místnosti. V tomto případě nejde o ekvidistantní data, protože hodnoty se liší o pět či deset vteřin. Data jsou v tabulce Datové soubory Tabulka 9 a na obrázku Jádrové odhady regresní funkce 16 a). Chceme odhadnout funkci, která vyjadřuje závislost axiální délky krystalů na čase.

Odhady vyhlazovacích parametrů podle metody křížového ověřování a pomocí automatické procedury:

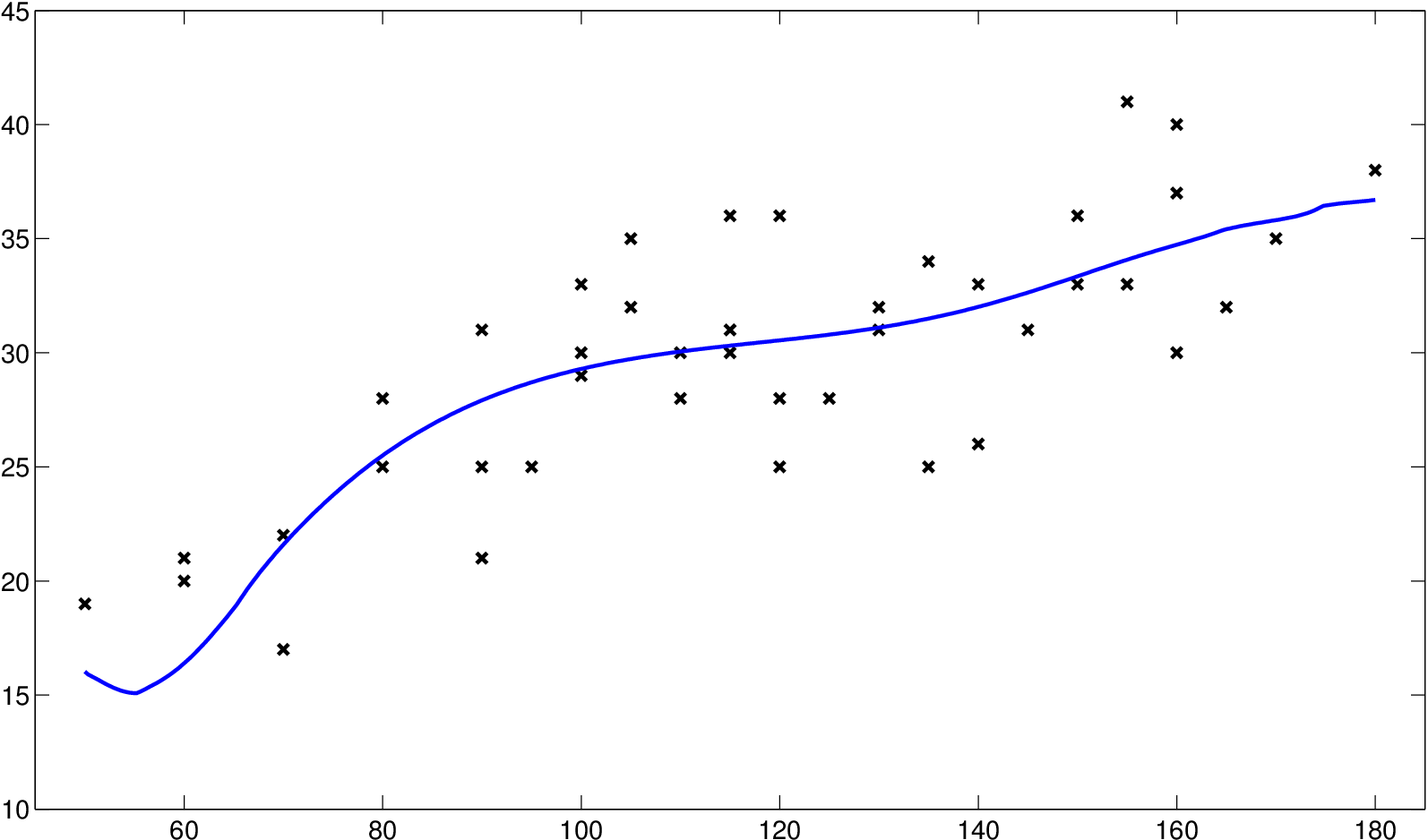
Výsledné odhady regresní funkce jsou na obrázku Jádrové odhady regresní funkce 16. Je vidět, že metoda křížového ověřování dává spíš podhlazený odhad. Na druhou stranu, odhad pomocí procedury se může zdát již přehlazený.

a) Data
b) hCV=0.1865, Kopt,0,2	c)  hCV=0.8826, Kopt,0,10
Obr. 16. Axiální délka krystalů ledu - data a odhadnuté regresní funkce, na ose x je vynesen čas ve vteřinách a na ose y délka krystalu v mikrometrech