Pokud jde o historii neparametrických metod, připomeňme, že v r. 1857 saský ekonom Engel analyzoval data týkající se nákladů na domácnost a pro vyjádření závislosti použil schodovitou (tj. po částech konstantní funkci), kterou dnes nazýváme regresogram. Regresogram užívá stejné základní myšlenky jako histogram pro odhad hustoty. Tato myšlenka spočívá v rozdělení množiny hodnot proměnné na intervaly a za odhad v bodě se vezme průměr hodnot na tomto subintervalu, tj.

kde je indikátorová funkce subintervalu

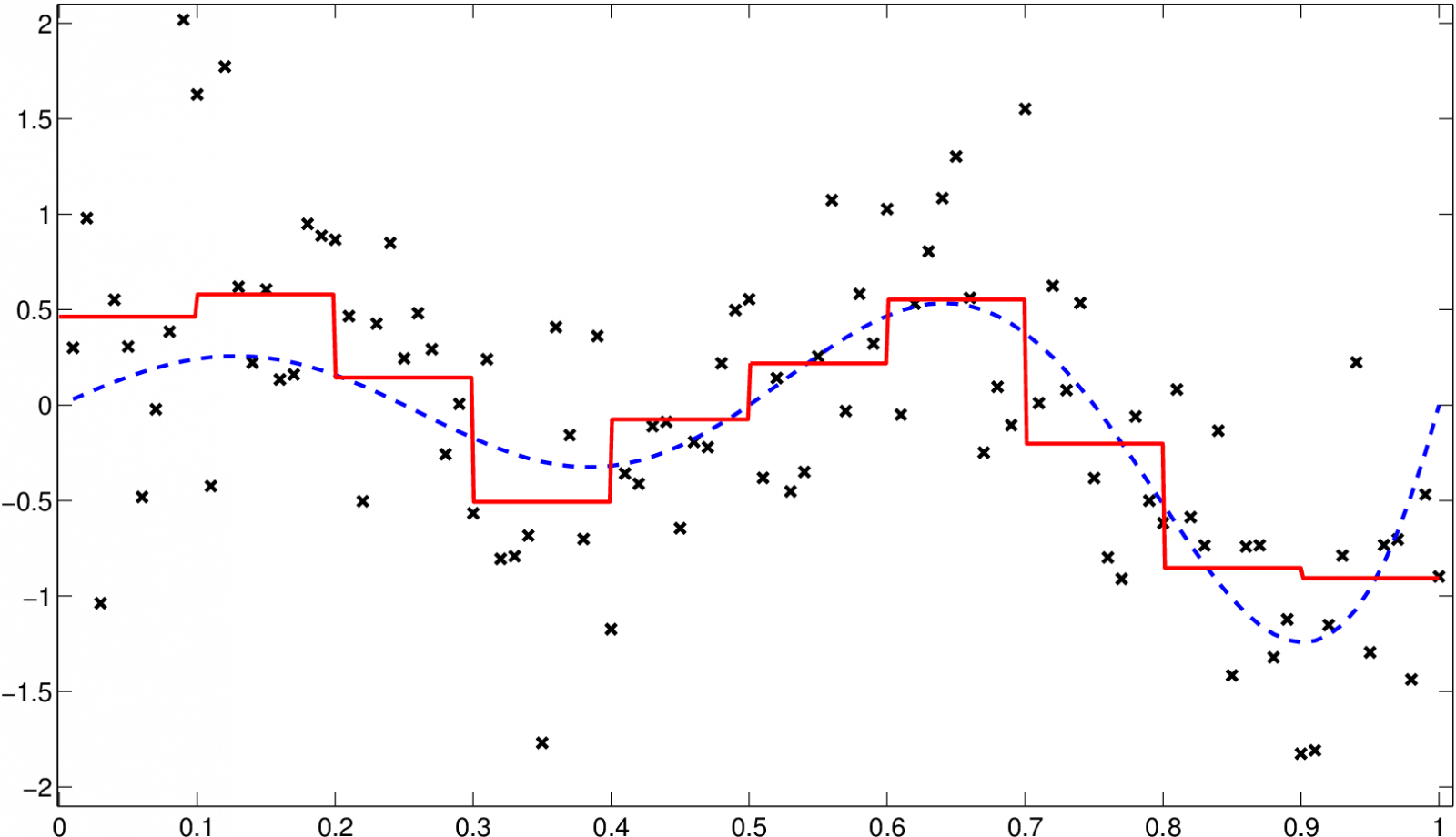
Výsledek aplikace regresogramu na simulovaná data z příkladu Jádrové odhady regresní funkce 1.2 je znázorněn na následujícím obrázku. Vidíme, že tento odhad „vhodně“ vystihuje tvar funkce, ale výsledný odhad je příliš hrubý.

Obr. 3. Regresogram (červená, plná) pro simulovaná data z příkladu 2.1 s původní funkcí (modrá, čárkovaná)

Přirozeným zobecněním regresogramu je metoda klouzavých průměrů. Tato metoda používá lokálních průměrů hodnot ale odhad v bodě je založen na centrovaném okolí bodu přesněji

(3)

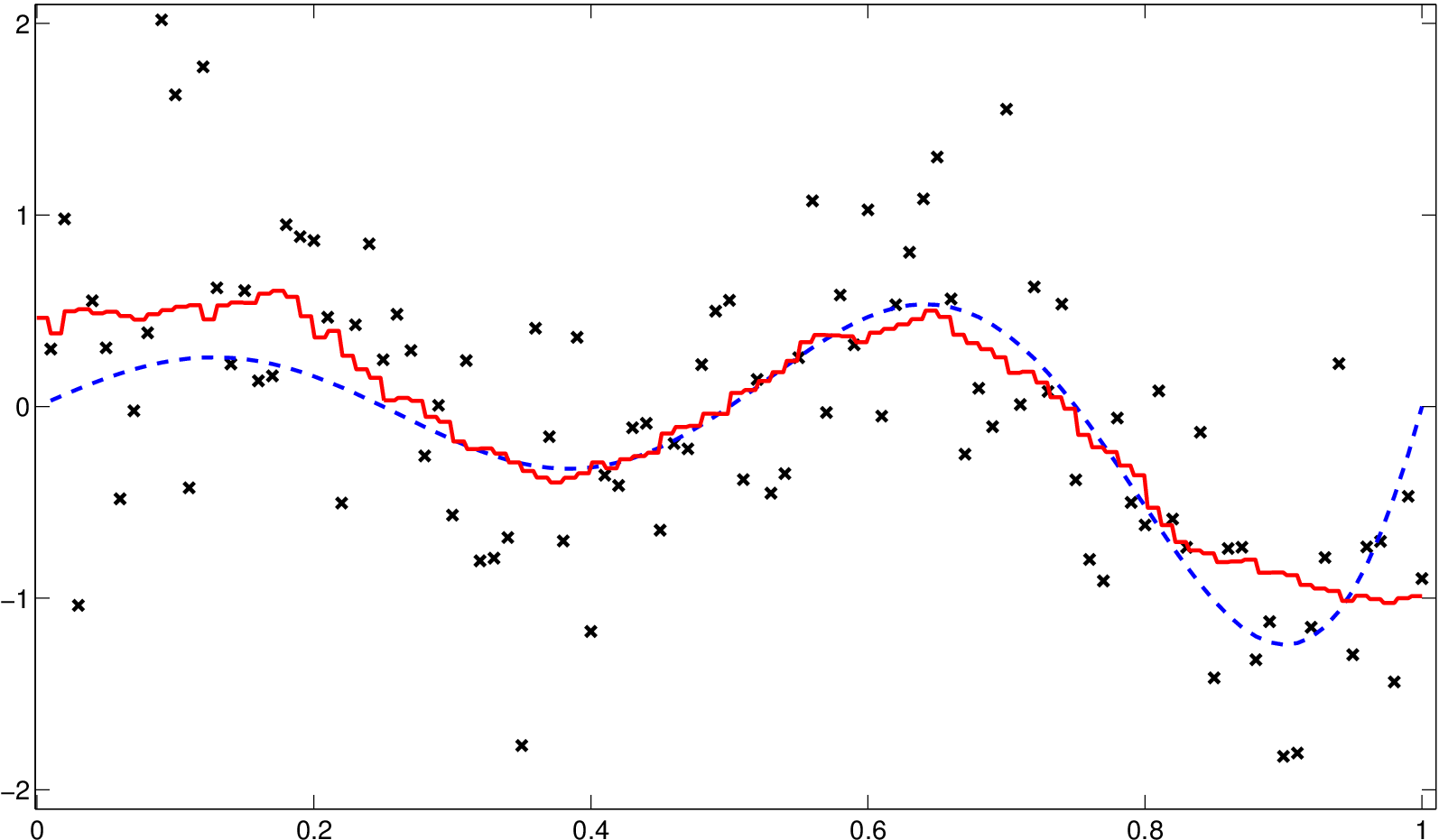
Obr. Jádrové odhady regresní funkce 4 ilustruje aplikaci této metody na simulovaných datech příkladu Jádrové odhady regresní funkce 1.2.

Obr. 4. Klouzavý průměr (červená, plná) pro simulovaná data z Jádrové odhady regresní funkce 1.2 s původní funkcí (modrá, čárkovaná)

Uvedené metody patří mezi nejjednodušší neparametrické vyhlazovací metody. Jádrové odhady lze považovat za zobecnění těchto metod.

Připomeňme zde základní myšlenku vyhlazování tak, jak ji formuloval R. Eubank v r. 1988:

Jestliže předpokládáme, že je hladká funkce, pak pozorování v bodech blízko bodu obsahují informace o hodnotě v bodě Bylo by tedy vhodné užít lokálních průměrů dat blízko bodu abychom získali odhad

Obecně lze jádrové odhady regresní funkce v bodě definovat takto

(4)

kde funkce se nazývají váhy, nezávisí na hodnotách ale závisí na kladném čísle které se nazývá vyhlazovací parametr (nebo také šířka vyhlazovacího okna). Speciální, velmi užitečný typ vah, závisí na jádrové funkci

Nechť je sudé číslo, položme Mezi nejznámější typy jádrových odhadů regresní funkce patří ([8]):

1.	Nadarayovy-Watsonovy odhady (1964)
2.	Priestleyovy-Chaovy odhady (1972)
3.	lokálně lineární odhady (Stone 1977, Cleveland 1979) kde
4.	Gasserovy-Müllerovy odhady (1979) kde Tento odhad je konvolučním typem odhadu.

Úmluva. Uvedené jádrové odhady budeme zapisovat ve tvaru

kde index značí příslušný typ odhadu s danou váhovou funkcí.

V mnoha aplikacích je užitečný zejména Nadarayův-Watsonův odhad Popíšeme nyní jeho konstrukci a budeme ilustrovat vliv vyhlazovacího parametru na kvalitu odhadu. Pro daný bod jsou váhy Nadarayova-Watsonova odhadu dány vztahem

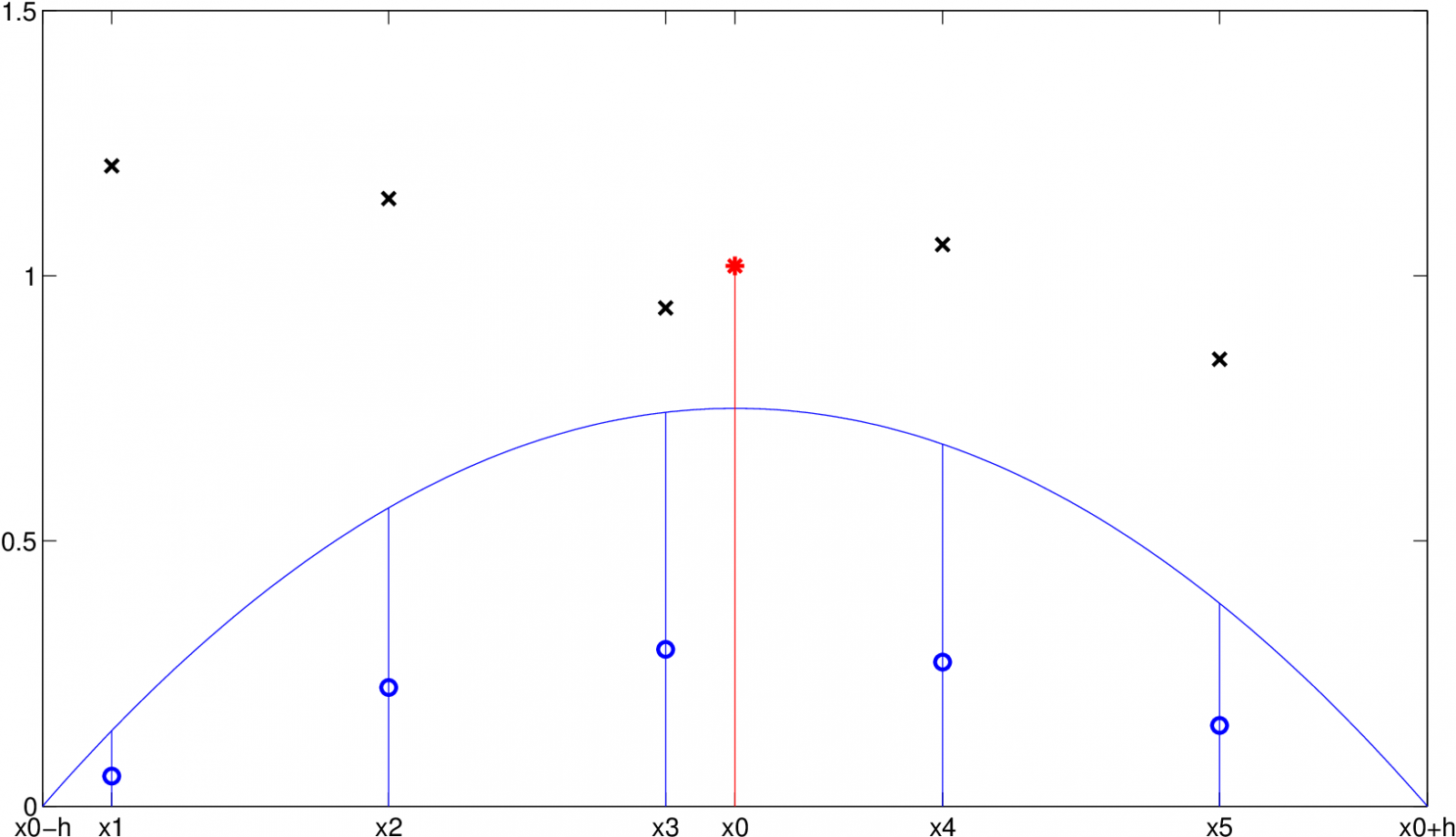
Obrázek Jádrové odhady regresní funkce 5 ilustruje konstrukci odhadu v bodě který je založen na pěti pozorováních (černé křížky). Parabola reprezentuje Epanečnikovo jádro a kroužky znázorňují hodnoty vah

pro Výsledný odhad regresní funkce v bodě je označen hvězdičkou.

Obr. 5. Ilustrace Nadarayova-Watsonova odhadu v bodě x₀

Otázka. Popište konstrukci Nadarayova-Watsonova odhadu, použijeme-li obdélníkové jádro místo Epanečnikova jádra. Vypočtěte váhy pro odhad s obdélníkovým jádrem.

Řešení

Obdélníkové jádro: pro Váhy Nadarayova-Watsonova odhadu:

Tedy NW odhad s obdélníkovým jádrem je totožný s klouzavým průměrem (viz obr. Jádrové odhady regresní funkce 7b)).

Jádrový odhad není definován pro Jestliže nastane případ „0/0“, pak klademe Omezíme se nyní na odhady funkce v bodech plánu

Pro malé hodnoty je výraz pro a tedy hodnota jádra v těchto bodech je rovna nule, a pro bod dostáváme odhad

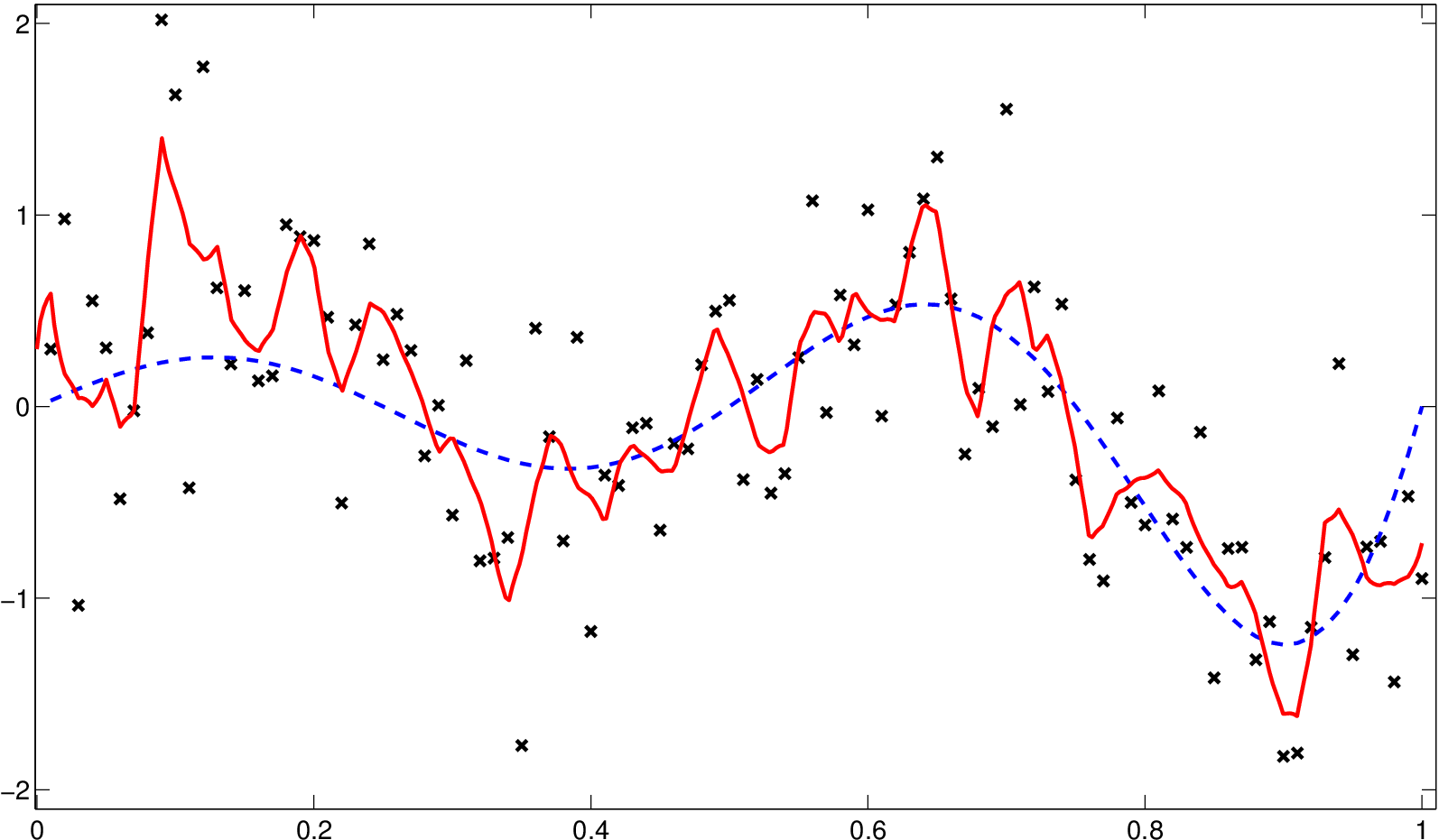
To znamená, že při malé šířce vyhlazovacího okna odhad reprodukuje data (viz obr. Jádrové odhady regresní funkce 6a)).

Podobně pro velké hodnoty je výraz tedy pro všechny body plánu je hodnota jádrové funkce a dostaneme tak průměr dat

Tedy velká šířka okna vede k přehlazení, a to k průměru dat (viz obr. Jádrové odhady regresní funkce 6b)).


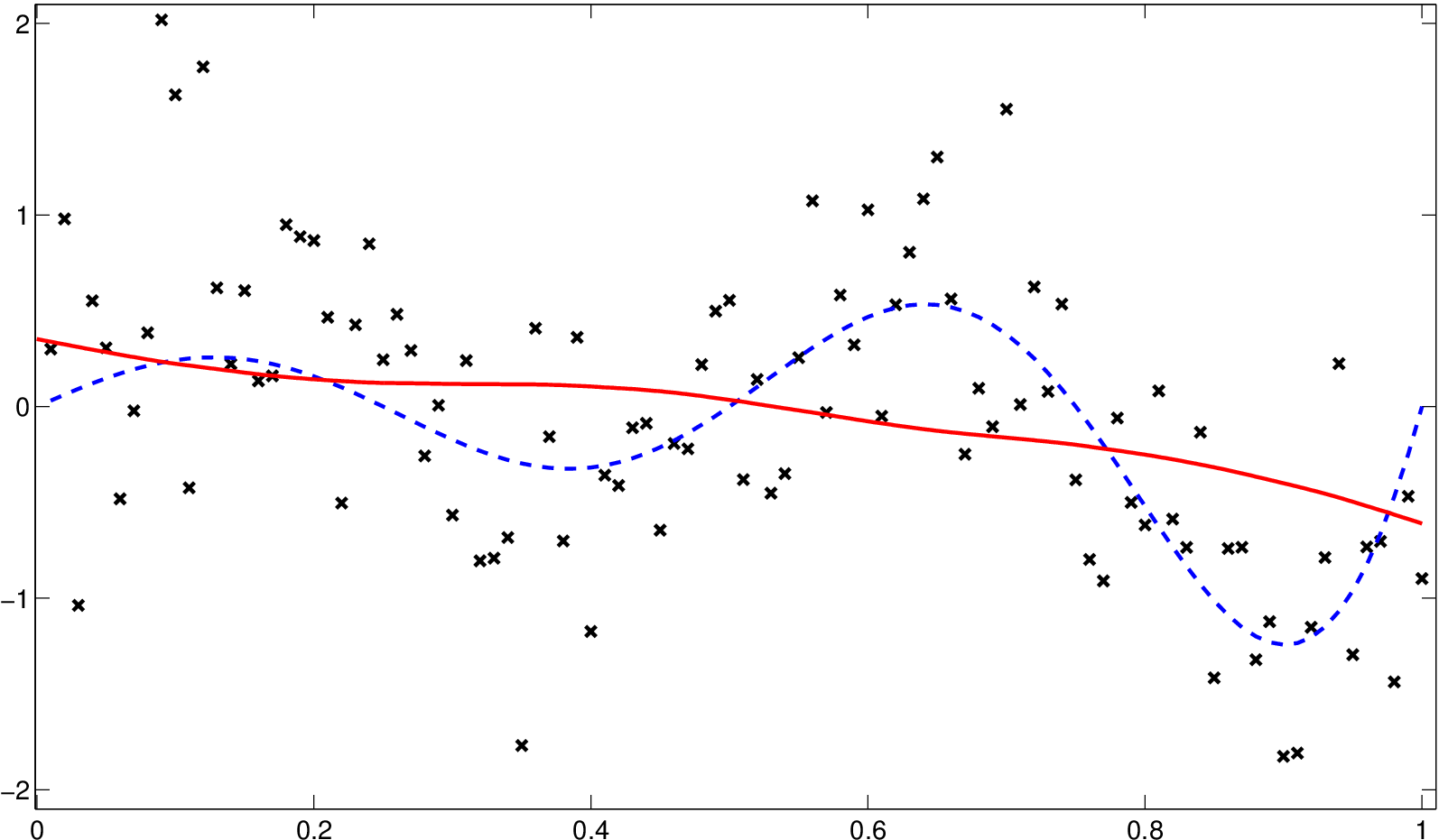
a) Podhlazený odhad, h=0,02	b) Přehlazený odhad, h=0,4
Obr. 6. Podhlazený a přehlazený odhad (červená, plná) regresní funkce (modrá, čárkovaná) z příkladu Jádrové odhady regresní funkce 1.2


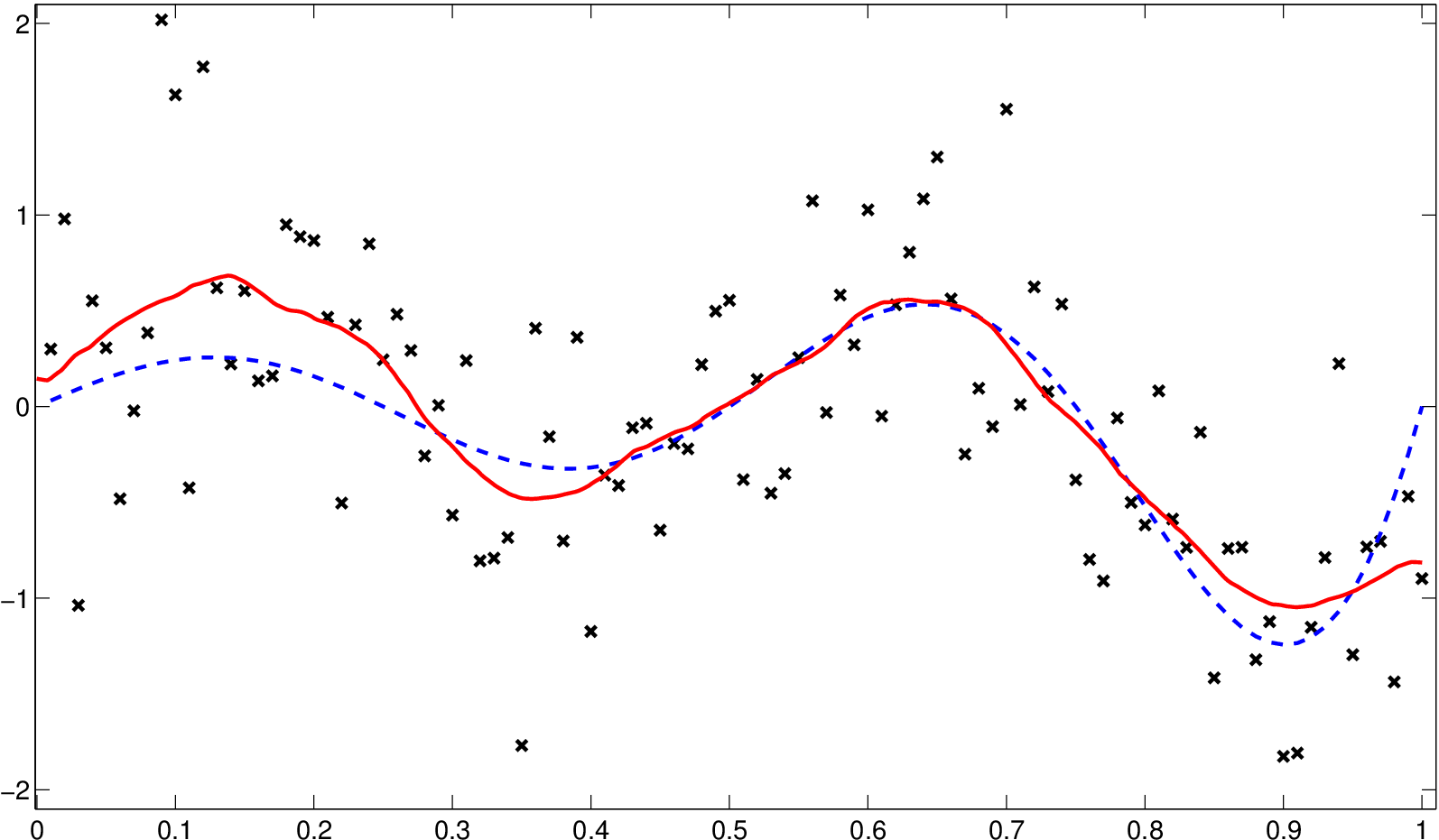
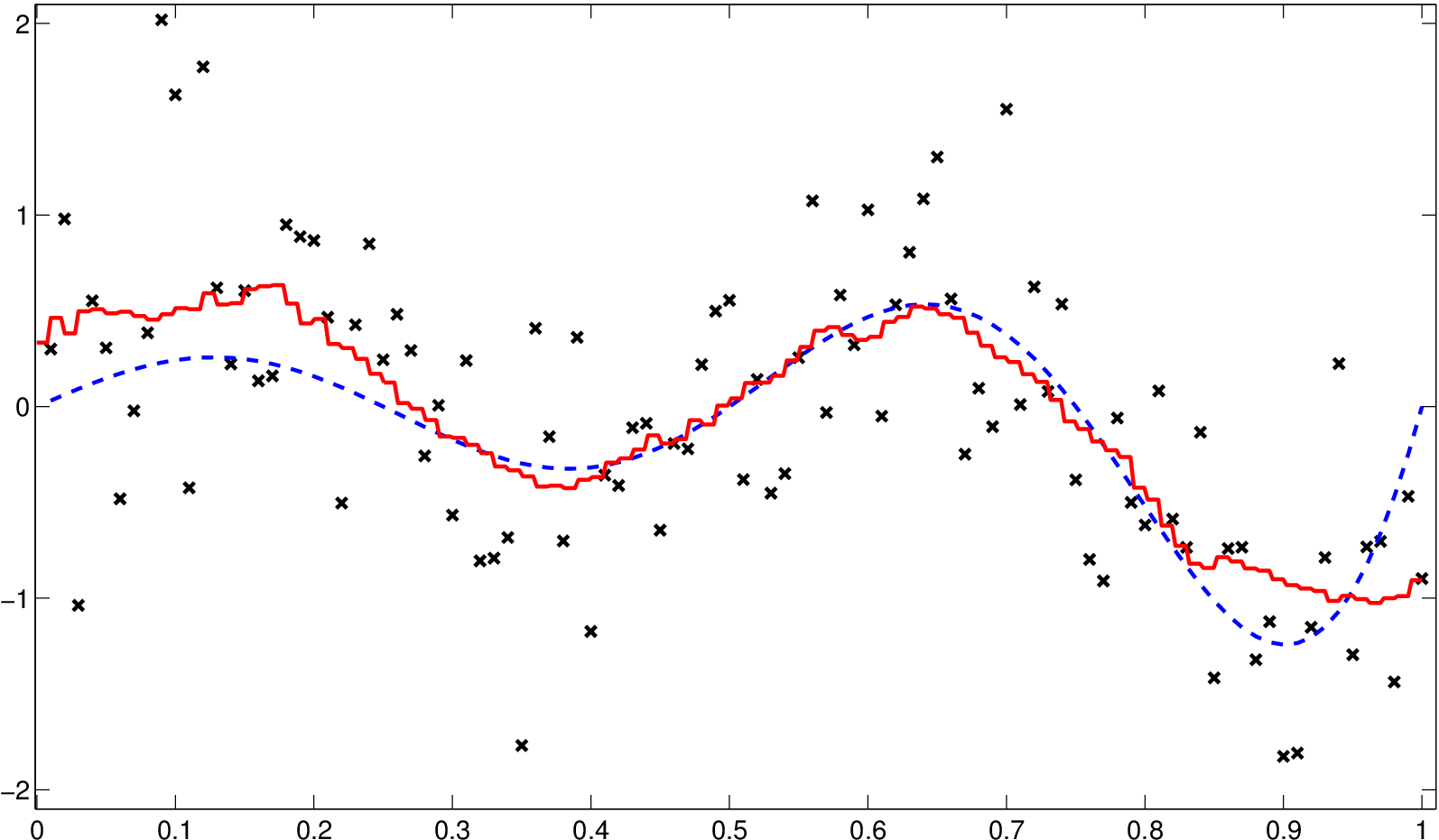
a) Odhad s Epanečnikovým jádrem a h=0,08	b) Odhad s obdélníkovým jádrem a h=0,09
Obr. 7. Odhady (červená, plná) regresní funkce (modrá, čárkovaná) z příkladu Jádrové odhady regresní funkce 1.2 s Epanečnikovým a obdélníkovým jádrem

Na obrázku Jádrové odhady regresní funkce 7a) je znázorněn odhad s Epanečnikovým jádrem. Tento odhad se nejvíce blíží skutečné regresní funkci. Pokud jde o volbu vyhlazovacího parametru, je třeba si uvědomit, že konečné rozhodnutí o odhadované křivce je částečně subjektivní, neboť i asymptoticky optimální odhady obsahují poměrně značné „množství šumu“ a to nechává prostor pro subjektivní posouzení.

Poznámka 2.1. Intervaly spolehlivosti pro hodnotu regresní funkce v bodě jsou užitečné v mnoha aplikacích. Bodový interval spolehlivosti udává interval, v němž s pravděpodobností leží hodnota funkce v bodě . Jsou definovány takto

kde je -kvantil standardního normálního rozdělení a odhad rozptylu v bodě je dán vztahem

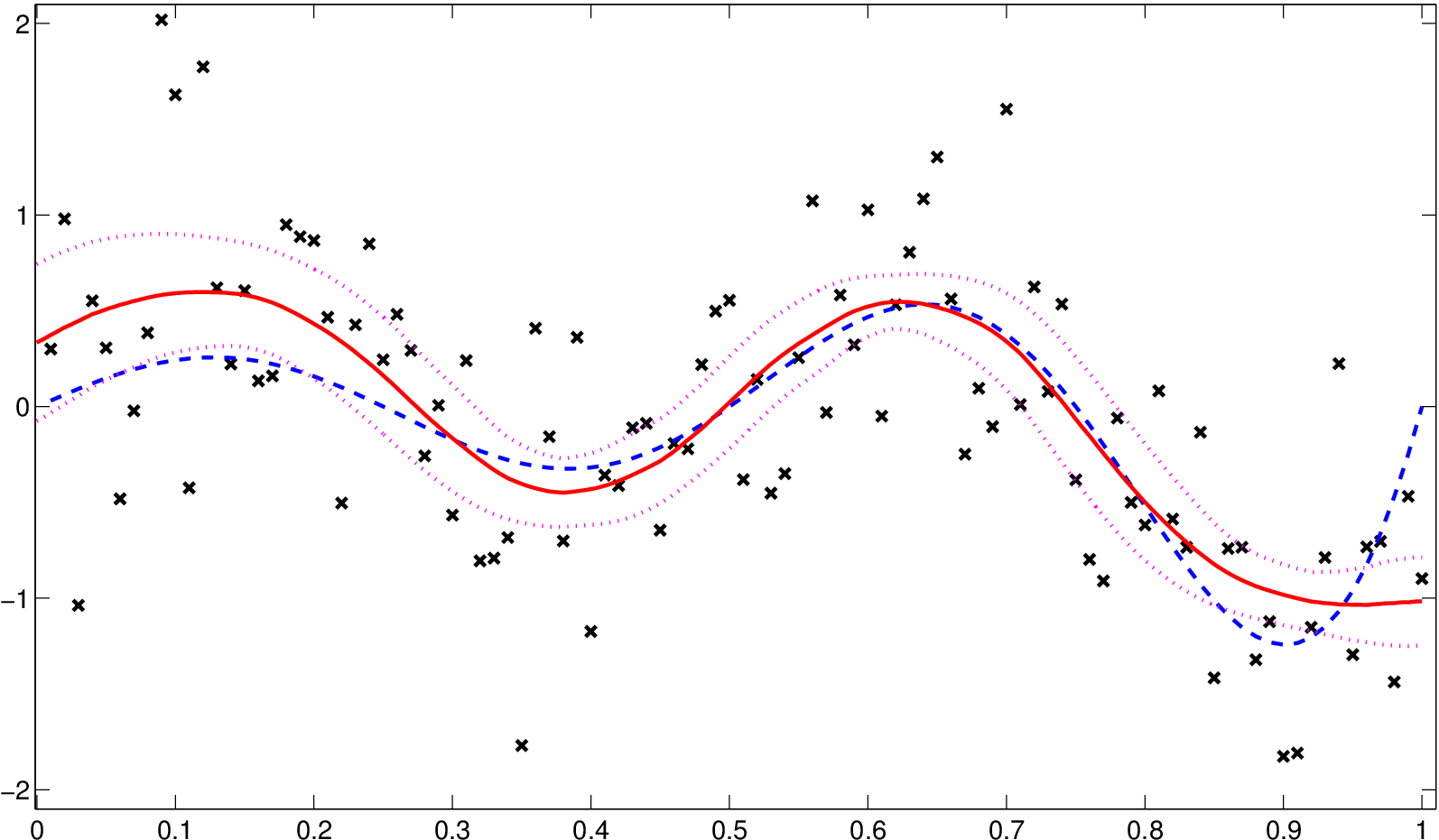
Ukázka intervalu spolehlivosti pro je na obrázku Jádrové odhady regresní funkce 8.

Obr. 8. Interval spolehlivosti pro data z příkladu Jádrové odhady regresní funkce 1.2 při α =0,05 (růžová, tečkovaná) se zobrazeným odhadem regresní funkce (červená, plná) a původní funkcí (modrá, čárkovaná)

vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity