Motivace

Uvažujme datový soubor, který obsahuje měření úrovně hladiny Huronského jezera. Huronské jezero je druhé největší jezero v systému pěti velkých jezer v Severní Americe. Jezerem prochází státní hranice mezi Kanadou a USA.¹

Měření byla prováděna ročně, v letech 1875 až 1972, a výsledky měření jsou zobrazeny na obrázku Jádrové odhady regresní funkce 1. Naším cílem je najít funkci popisující úroveň hladiny v uvedených letech.

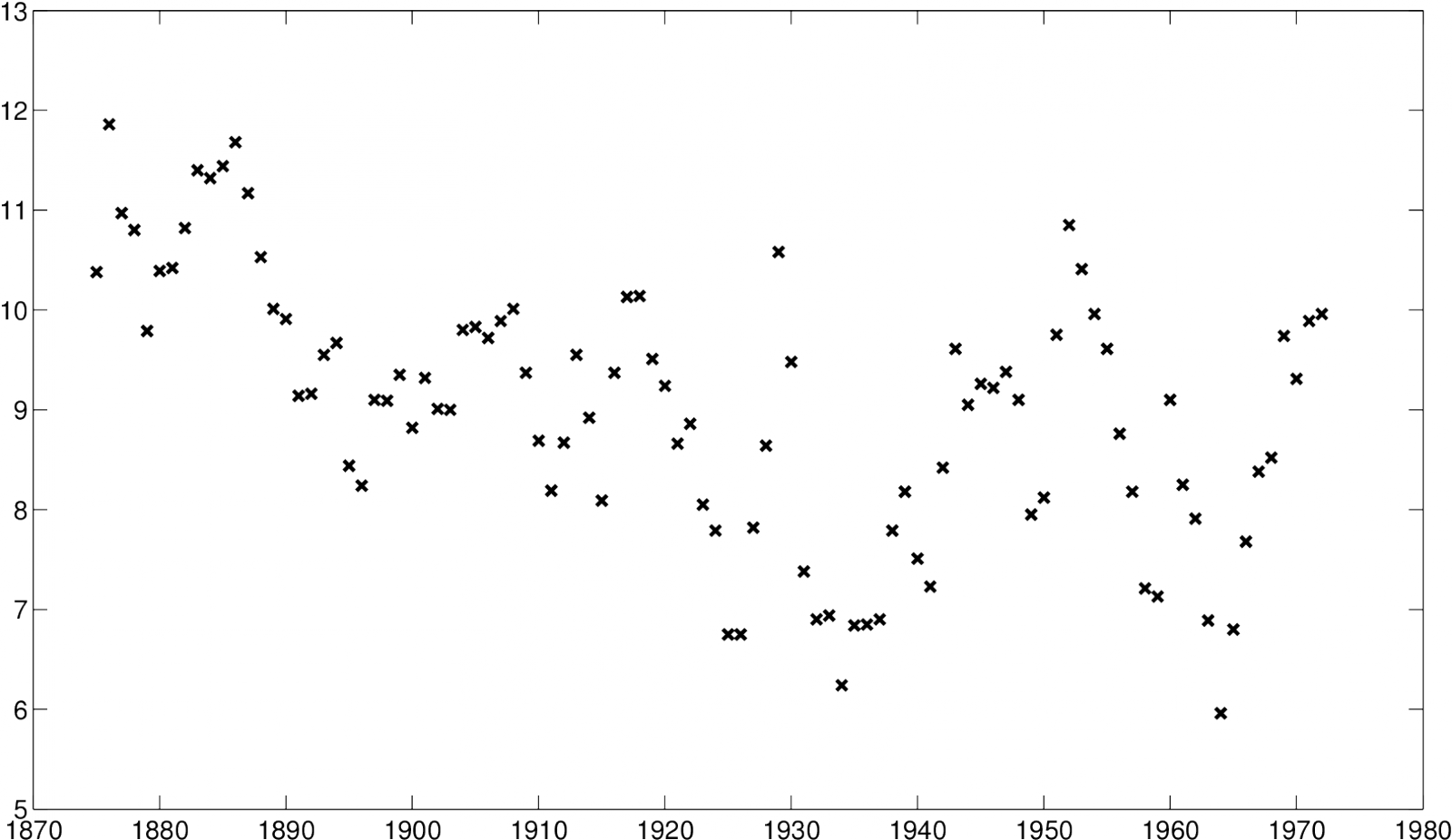Vidíme, že pouhý pohled na tento dvourozměrný bodový diagram obvykle nestačí k tomu, abychom určili tento funkční vztah. 

Statistická úloha, kterou se budeme zabývat, spočívá v proložení vhodné křivky těmito body tak, aby byly odfiltrovány náhodné výkyvy a bylo možné lépe poznat strukturu dat. Tuto křivku nazýváme regresní křivkou.

Formalizujme nyní tuto úlohu: Uvažujme standardní regresní model

(1)

kde je neznámá regresní funkce, jsou body plánu, jsou hodnoty závisle proměnné a jsou chyby měření, o nichž se předpokládá,  že jsou nezávislými, identicky rozdělenými náhodnými veličinami splňujícími podmínky

(2)

Poznámka 1.1. Jsou-li body plánu uspořádaná nenáhodná čísla, mluvíme o regresním modelu s pevným plánem. V případě, že body plánu  jsou náhodné veličiny se stejnou hustotou jedná se o regresní model s náhodným plánem (podrobněji např. [14]). Budeme se dále zabývat modelem s pevným  plánem.

Bez újmy na obecnosti budeme v dalším předpokládat, že pro body platí

Cílem regresní analýzy je nalézt vhodnou aproximaci neznámé funkce . Tento proces odhadu  regresní funkce se obvykle nazývá vyhlazování. K tomuto úkolu lze přistoupit  dvěma způsoby - parametricky a neparametricky. Příkladem parametrického odhadu regresní funkce je regresní přímka vyjadřující lineární závislost. Naopak u neparametrického přístupu nepředpokládáme, že funkce má nějaký předepsaný tvar, pouze předpokládáme jistou hladkost odhadované funkce (tj. dostatečný počet spojitých derivací).

V první polovině dvacátého století byla věnována pozornost zejména parametrickým metodám. V posledních letech však zaznamenaly značný rozvoj neparametrické metody. Tento vývoj souvisí s rostoucími požadavky na zpracování dat, ať už jde o rozsah souborů, rozmanitost těchto dat apod. Čistě parametrický přístup nevyhovuje vždy potřebám flexibility a nebývalý rozmach výpočetní techniky vytvořil dobré předpoklady pro rozvoj neparametrických metod. I přes tento vývoj si oba způsoby zachovávají své výhody a nijak si  nekonkurují. Někdy je vhodné užít neparametrické metody a pak na výsledný odhad použít parametrickou metodu.

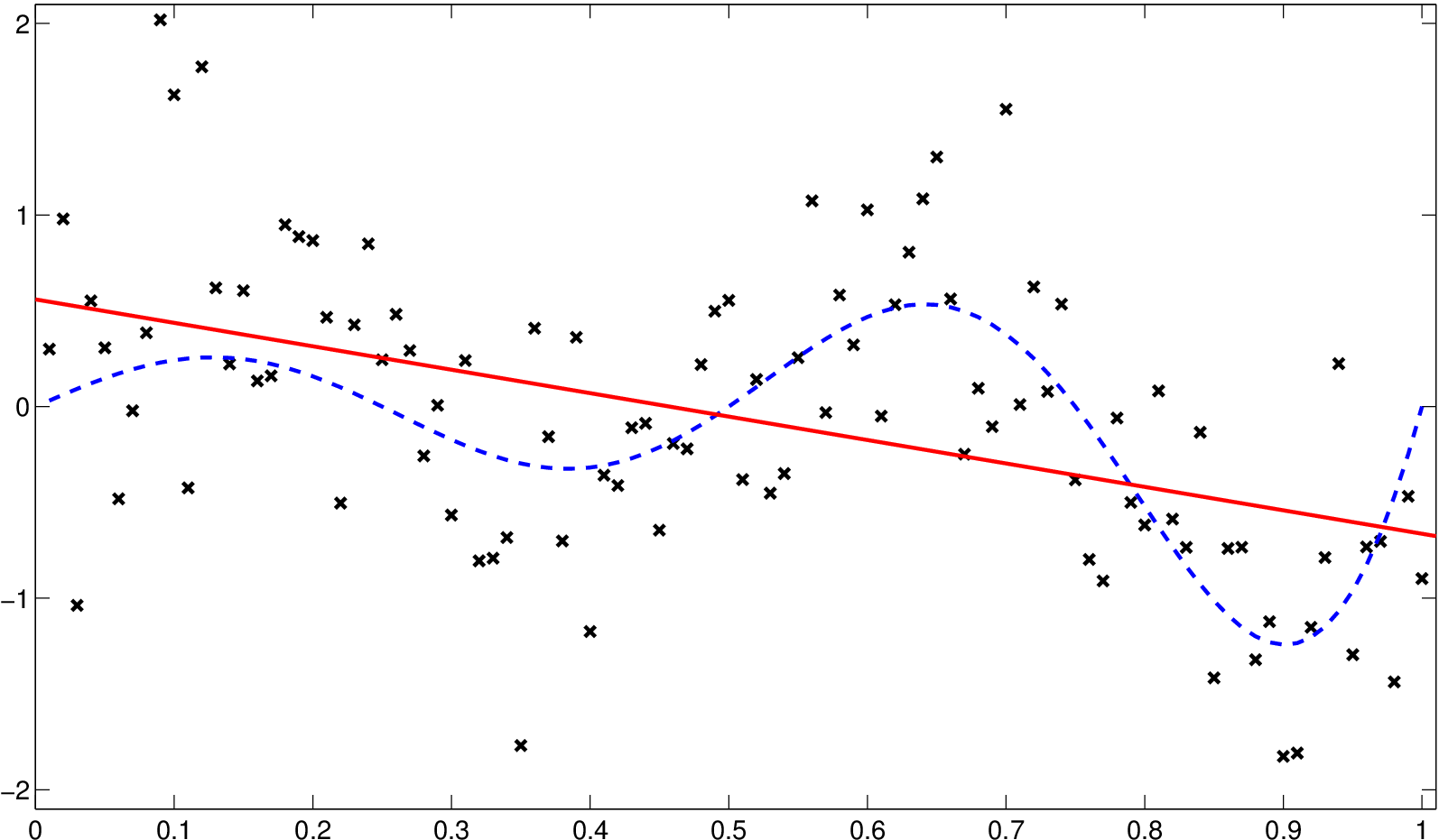
Příklad 1.2. Obr. Jádrové odhady regresní funkce 2 ilustruje na simulovaných datech nevhodnost aplikace parametrického přístupu. V tomto případě byla data generována podle vztahu

kde body a chyby mají normální rozdělení N(0; 0,25). (Data jsou v tabulce Datové soubory Tabulka 1.)

Obr. 2. Simulovaná data () s regresní přímkou (červená, plná) a původní funkcí (modrá, čárkovaná)

Předpokládejme, že hledaná křivka je přímka a známou metodou nejmenších čtverců určíme rovnici této přímky. Obr. Jádrové odhady regresní funkce 2 znázorňuje přesnou funkci, generovaná data a výslednou přímku. Je zřejmé, že náš předpoklad, že hledaná funkce je přímka, není správný.

¹„Great Lakes from space“ od SeaWiFS Project, NASA/Goddard Space Flight Center, and ORBIMAGE.-visibleearth.nasa.gov/view_rec.php?id=793. Licencováno pod Public domain via Wikimedia Commons.