Statistické vlastnosti odhadu

Kvalitu jádrového odhadu lze lokálně popsat pomocí střední kvadratické chyby

Spočítejme nejdříve hodnotu v bodě

Předpokládejme dále, že Označme první integrál a druhý Integrál počítáme metodou per partes a využijeme vlastnosti funkce

		(2)
Dále použijeme Taylorův rozvoj tedy

Počítejme nyní integrál

uvažujeme-li substituce dostaneme
		(3)

Vychýlení odhadu je tedy tvaru

Poznámka 3.1. Vztahy Jádrové odhady distribuční funkce (2) a Jádrové odhady distribuční funkce (3) dávají zajímavý vztah pro vychýlení

Odtud plyne

A dále (z Taylorova vzorce)

Nyní dokážeme tvar rozptylu.

Zde Počítáme tedy jen integrál (označme jej ):

První integrál počítáme metodou per partes a máme

použijeme nyní Taylorův rozvoj funkce
užitím vlastností funkce a dostaneme

Rozptyl je tedy tvaru

Výše uvedené výsledky můžeme nyní zformulovat v následující větě:

Věta 3.2. Nechť pro Pak

		(4)

Globální pohled na kvalitu odhadu lze získat prostřednictvím střední integrální kvadratické chyby

Věta 3.3. Nechť a Pak

(5)

kde

Naším cílem je nalézt takovou hodnotu vyhlazovacího parametru, pro kterou bude nabývat minimální hodnoty. Ale uvedený tvar není pro takovou analýzu vhodný, a proto (stejně jako při odhadu hustoty a regresní funkce) budeme uvažovat asymptotickou střední integrální kvadratickou chybu která v tomto případě je tvaru:

(6)

Nyní už lze standardními metodami matematické analýzy nalézt takovou hodnotu pro kterou nabývá minimální hodnoty. Je snadné ukázat, že

(7)

a pak

(8)

Poznámka 3.4. Optimální hodnota vyhlazovacího parametru pro odhad distribuční funkce je řádu zatímco pro odhad hustoty s jádrem je vyhlazovací parametr řádu

Příklad 3.5. Předpokládejme, že známe tvar distribuční funkce pro Vypočítejme hodnotu optimálního vyhlazovacího parametru pro odhad s jádrem řádu 2.

Podle vztahu Jádrové odhady distribuční funkce (7) potřebujeme spočítat hodnoty a S Epanečnikovým jádrem je

Pak

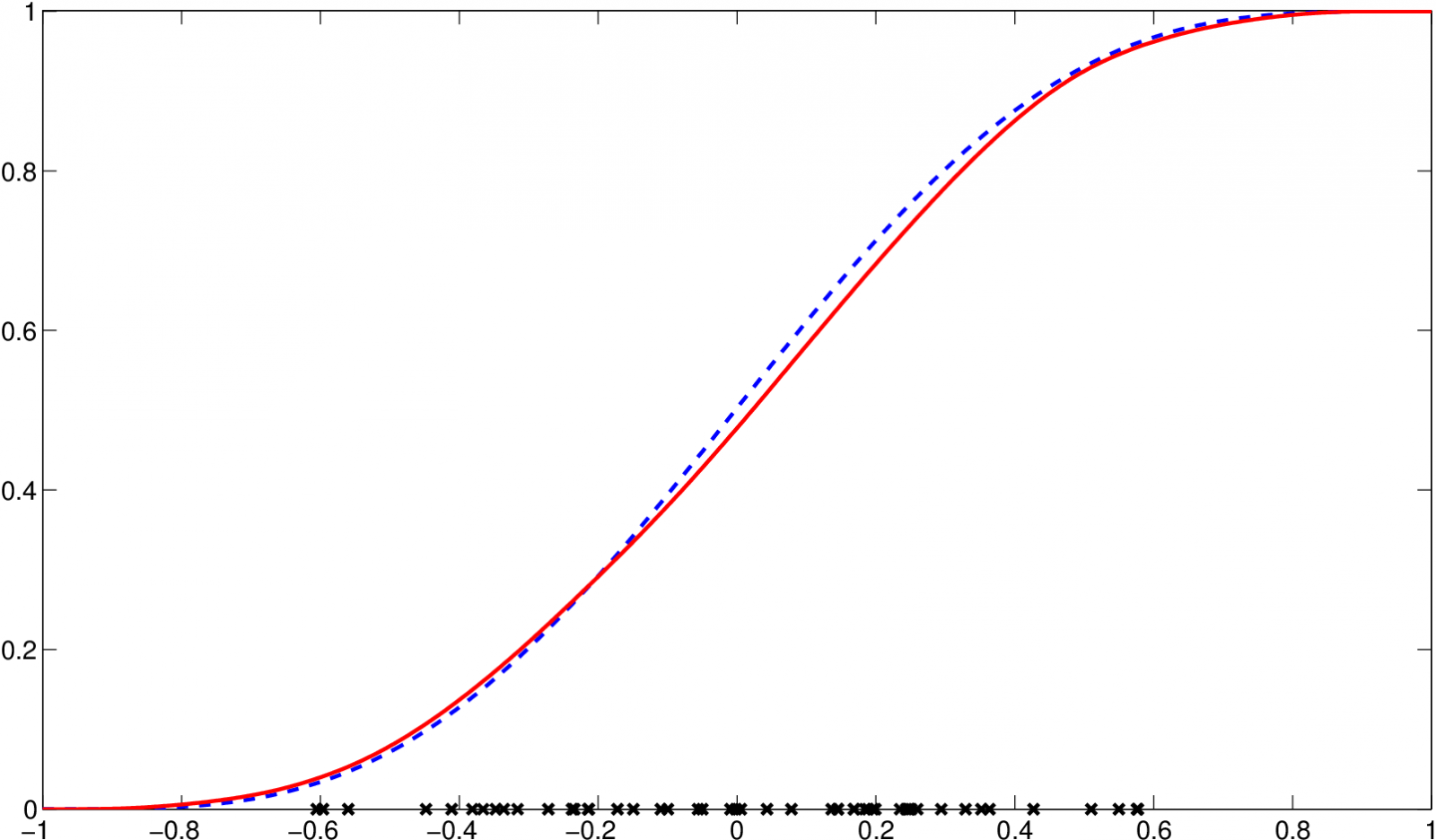
Na následujícím obrázku je odhad s optimálním vyhlazovacím parametrem pro náhodný výběr o 50 pozorování, která pochází z rozdělení s uvedenou distribuční funkcí (data jsou v tabulce Datové soubory Tabulka 4).

Obr. 5. Odhad distribuční funkce z ukázkového příkladu Jádrové odhady distribuční funkce 3.5, odhad (červená, plná) a původní funkce (modrá, čárkovaná) za použití Epanečnikova jádra a hopt,0,2=0,3432