Z dříve uvedených odhadů chyb je zřejmé, že kvalita jádrového odhadu závisí na šířce okna na jádře a na řádu jádra což je číslo, které odpovídá předpokládanému počtu derivací v odhadovaném modelu. Je zřejmé, že všechny tyto tři veličiny se vzájemně ovlivňují, a proto je třeba zabývat se jejich volbou současně.

Pro simultánní volbu jádra, optimálního vyhlazovacího parametru a řádu jádra byla navržena automatická procedura (viz [3]), která odhadne všechny parametry tak, aby byla minimalizována Procedura byla původně odvozena pro odhad hustoty pravděpodobnosti ([4]), ale lze ji aplikovat i pro odhad regresní funkce. Uvedeme zde její zjednodušenou verzi.

Podle vztahů Jádrové odhady regresní funkce (12) a Jádrové odhady regresní funkce (13) je tvaru

a tvaru

Ze vztahu pro vypočteme a dosadíme do vztahu pro Dále použijeme vztahy

a dostaneme vyjádření

ve kterém jsou parametry , a separovány, což umožňuje vybrat tyto parametry simultánně. Právě tento vztah je základem automatické procedury.

Položme

a množinu vhodných řádů označme

kde značí celou část čísla Procedura pak probíhá v pěti krocích:

Příklad 6.1. Aplikace procedury na data z příkladu Jádrové odhady regresní funkce 1.2. Maximální řád jádra zvolme tedy množina možných řádů jader je Pro tyto řády spočítejme hodnoty z kroků 1-3, v kroku 2 jsme použili metodu křížového ověřování pro nalezení optimálního vyhlazovacího parametru

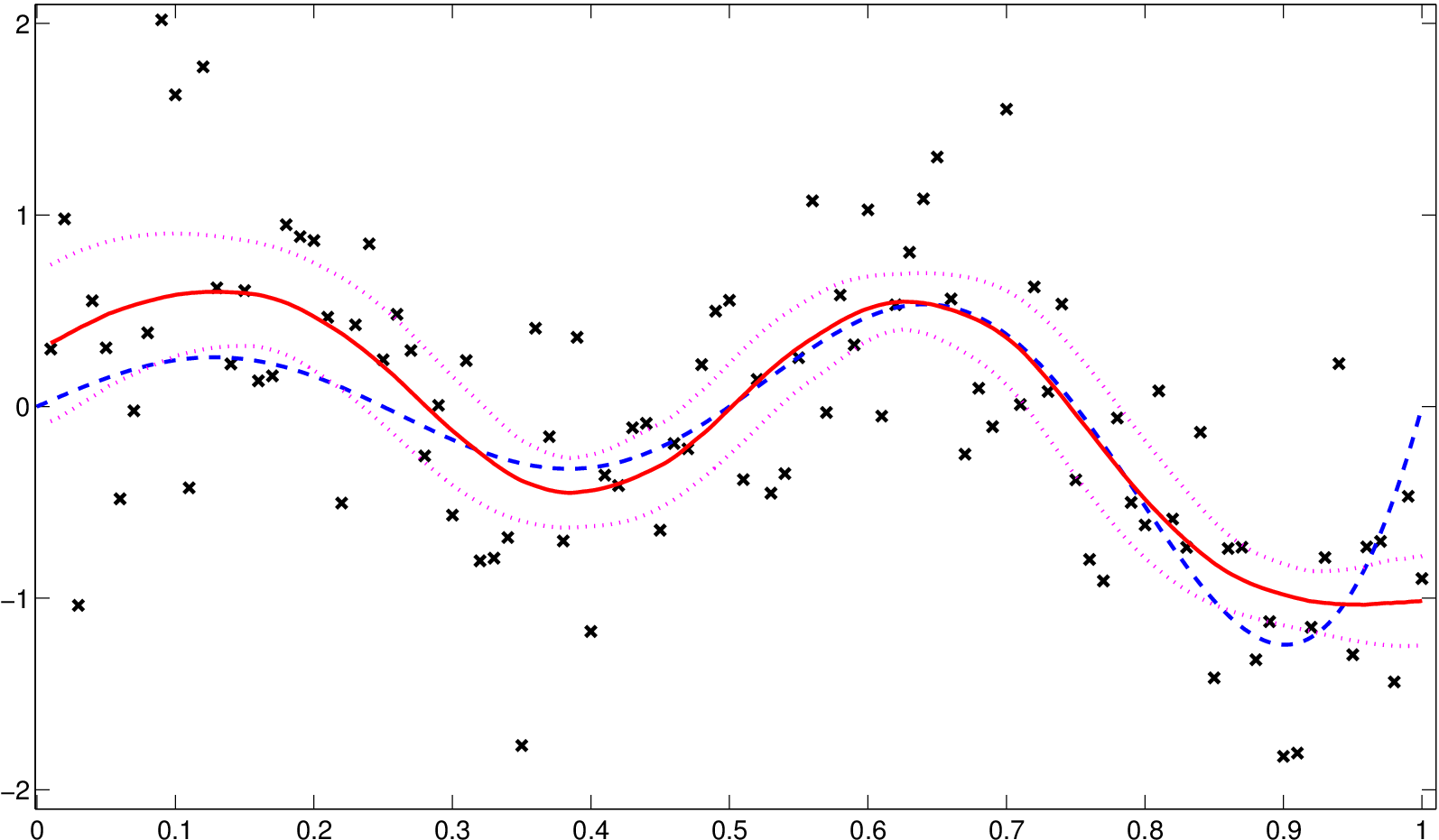
Z tabulky vidíme, že optimální řád jádra je Výsledný odhad je uveden na následujícím obrázku.

Obr. 14. Simulovaná data (x) s jádrovým odhadem regresní funkce při použití procedury (červená, plná) a skutečnou funkcí (modrá, čárkovaná) společně s 95% intervalem spolehlivosti (růžová, tečkovaná)