Základní typy odhadů

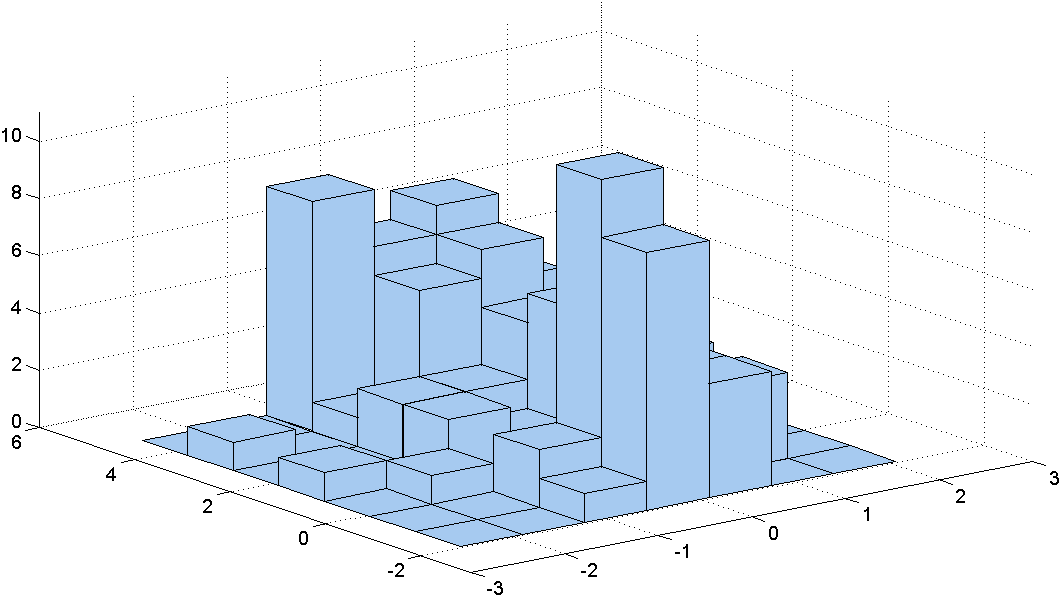
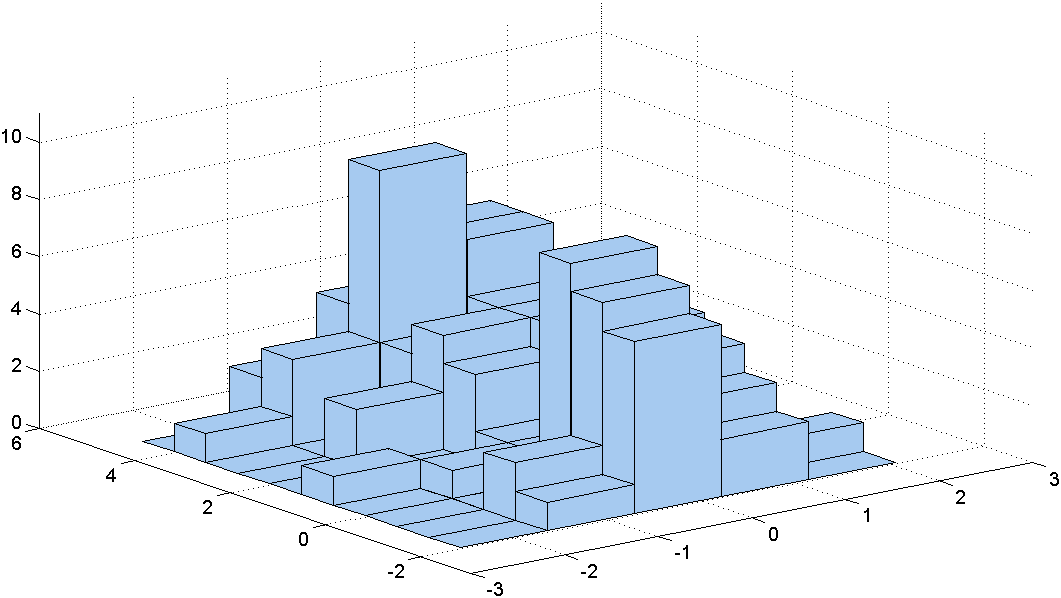
Podobně jako u odhadů hustoty můžeme použít histogram, ale ten má zmíněné nevýhody - jde o schodovitou funkci a je citlivý na volbu počtu a šířky třídicích obdélníků - viz obrázek Jádrové odhady dvourozměrných hustot 2.

Příklad 2.1. Mějme dán datový soubor o velikosti n=100 generovaný ze směsi tří normálních hustot¹. a (Data jsou v tabulce Datové soubory Tabulka 6.)

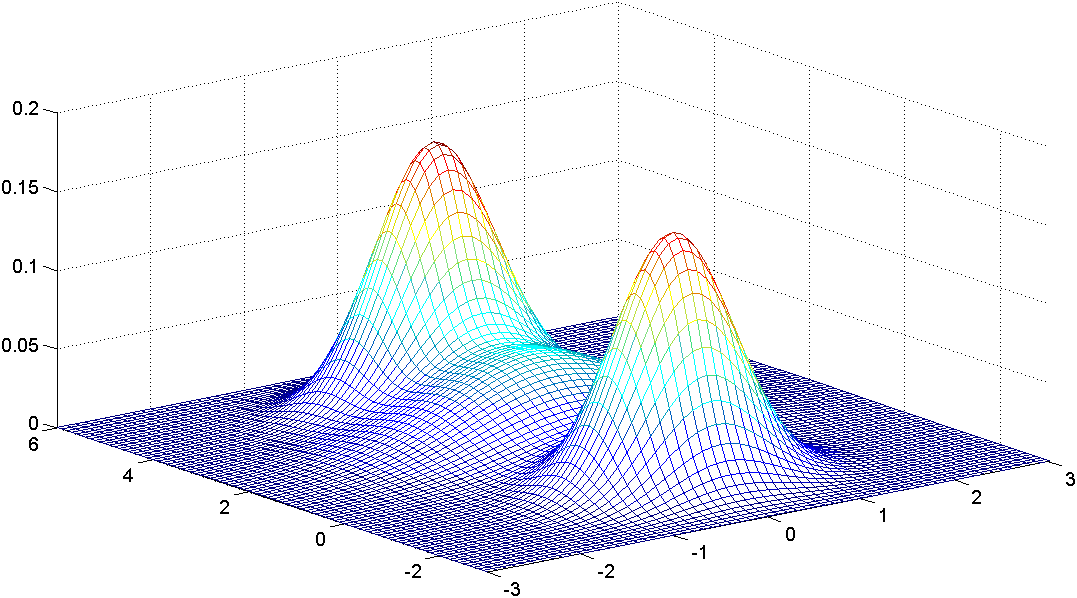
Z obrázků Jádrové odhady dvourozměrných hustot 2.a) a Jádrové odhady dvourozměrných hustot 2.b) je patrné, že histogram nepostihuje charakteristické rysy hustoty  pravděpodobnosti dat, která je zobrazena na obrázku Jádrové odhady dvourozměrných hustot 2.c).

a) 7 x 7 obdélníků	b) 5 x 10 obdélníků
c) Hustota simulovaných dat
Obr. 2. Histogramy s různými počty třídicích obdélníků a hustota pro data z příkladu Jádrové odhady dvourozměrných hustot 2.1

Přejdeme nyní k jádrovým odhadům dvourozměrné hustoty. Předpokládejme, že máme k dispozici náhodný výběr z dvourozměrného spojitého rozdělení s hustotou Jádrový odhad hustoty v bodě je definovaný vztahem

(1)

je dvourozměrné jádro a je pozitivně definitní matice typu a značí její determinant. Prvky matice se nazývají vyhlazovací parametry a matice se pak zkráceně označuje jako vyhlazovací matice.

Jádro je dvourozměrná funkce, kterou můžeme získat pomocí jednorozměrného symetrického jádra Existují dva typy těchto jader:

• součinové jádro

• sféricky symetrické jádro

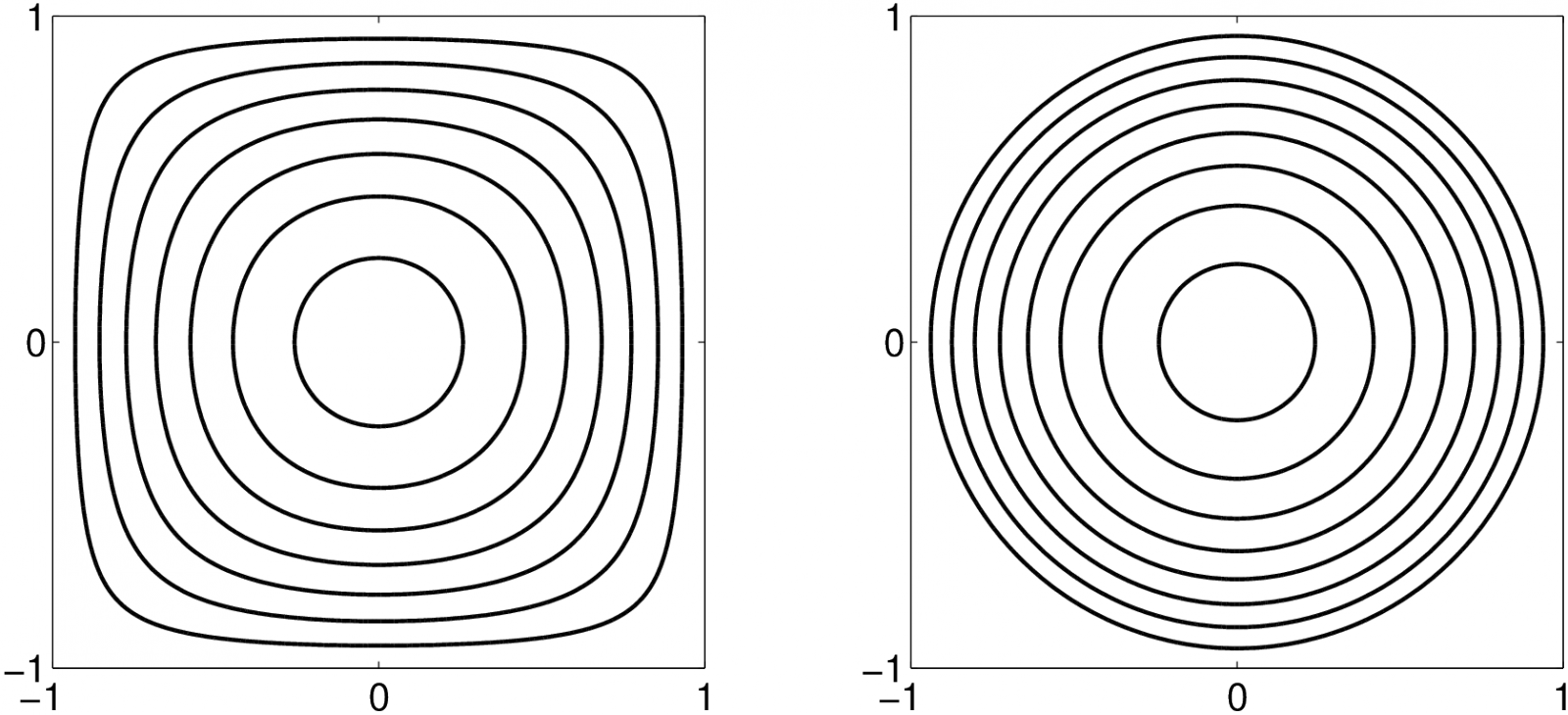
Příklad 2.2. Epanečnikovo jádro, které je v jednorozměrném případě tvaru má následující dvourozměrné varianty

Na následujícím obrázku jsou zobrazeny vrstevnice těchto jader.

Obr. 3. Součinové (vlevo) a sféricky symetrické (vpravo) dvourozměrné Epanečnikovo jádro

Poznámka 5.2. V praxi se často používá Gaussovo jádro

Kromě jeho výhod při výpočtech statistických vlastností odhadu, má navíc zajímavou vlastnost, a to, že je součinovým i sféricky symetrickým jádrem.

Podívejme se blíže na matici Jde o matici vyhlazovacích parametrů, které řídí hladkost výsledného odhadu. Navíc také udávají orientaci odhadnuté hustoty. Rozlišujeme tři základní třídy vyhlazovacích matic:

• třída která obsahuje matice s jediným vyhlazovacím parametrem,
• třída která zahrnuje diagonální matice,
• třída která obsahuje tzv. plné matice.

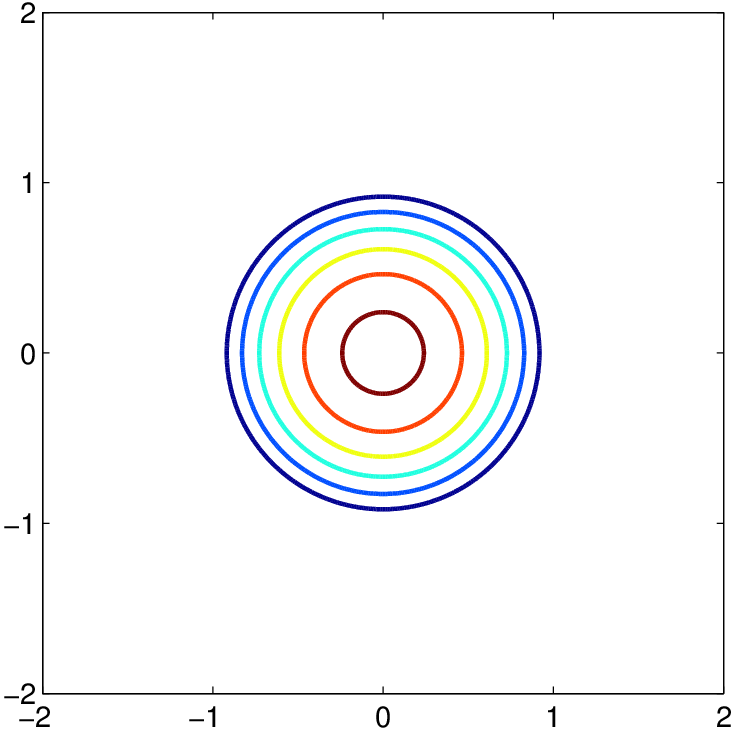
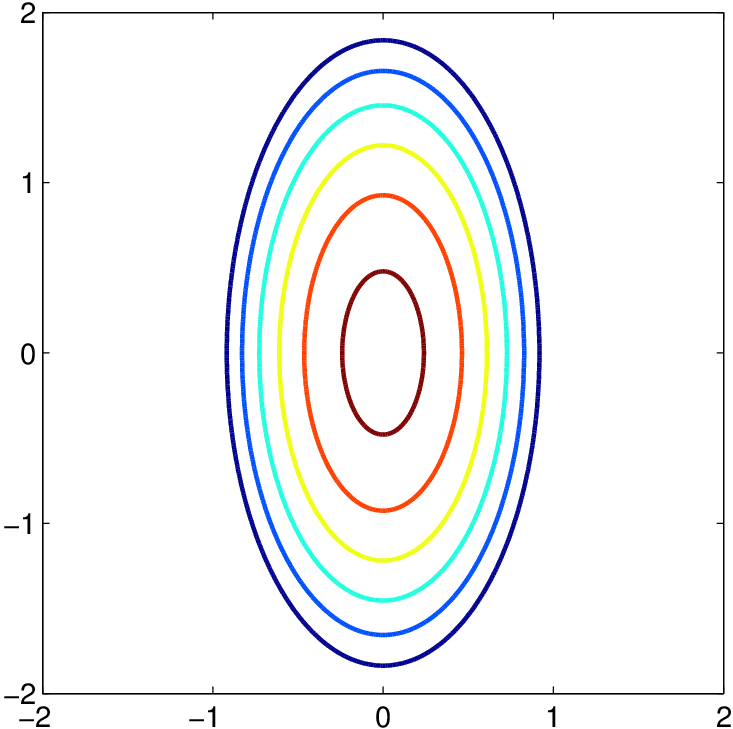
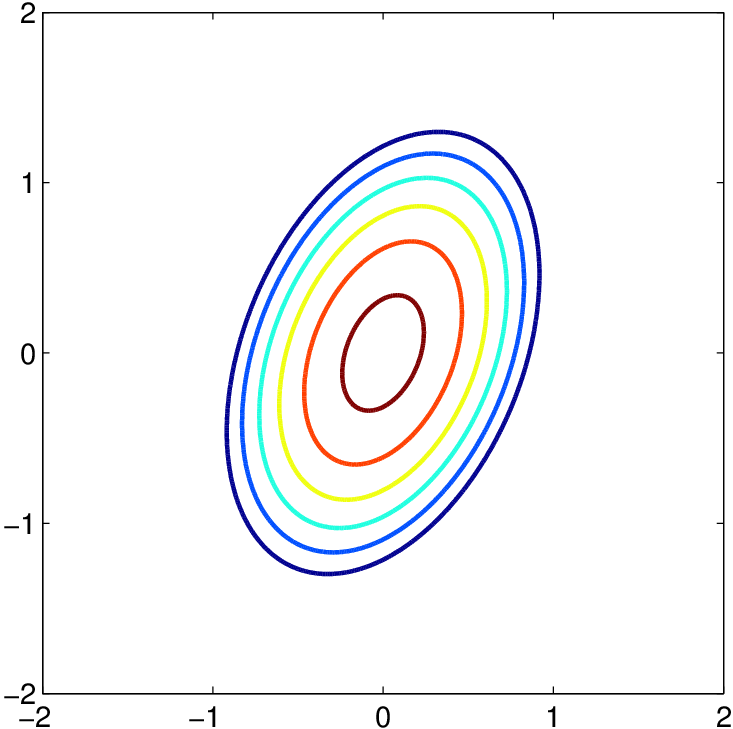
Rozdíly mezi jednotlivými maticemi jsou patrné z následující tabulky, kde jsou zobrazeny vrstevnice sféricky symetrického Epanečnikova jádra v závislosti na třídě matic.

Tab. 1. Třídy vyhlazovacích matic

Budeme se zabývat jádrovými odhady s diagonální vyhlazovací maticí. Jádrový odhad s maticí třídy dává ve všech směrech stejnou míru vyhlazení, což neponechává příliš mnoho prostoru pro zachycení variabilty dat. Na druhou stranu při použití matice třídy je potřeba odhadnout větší počet parametrů, což znamená vyšší výpočetní náročnost.

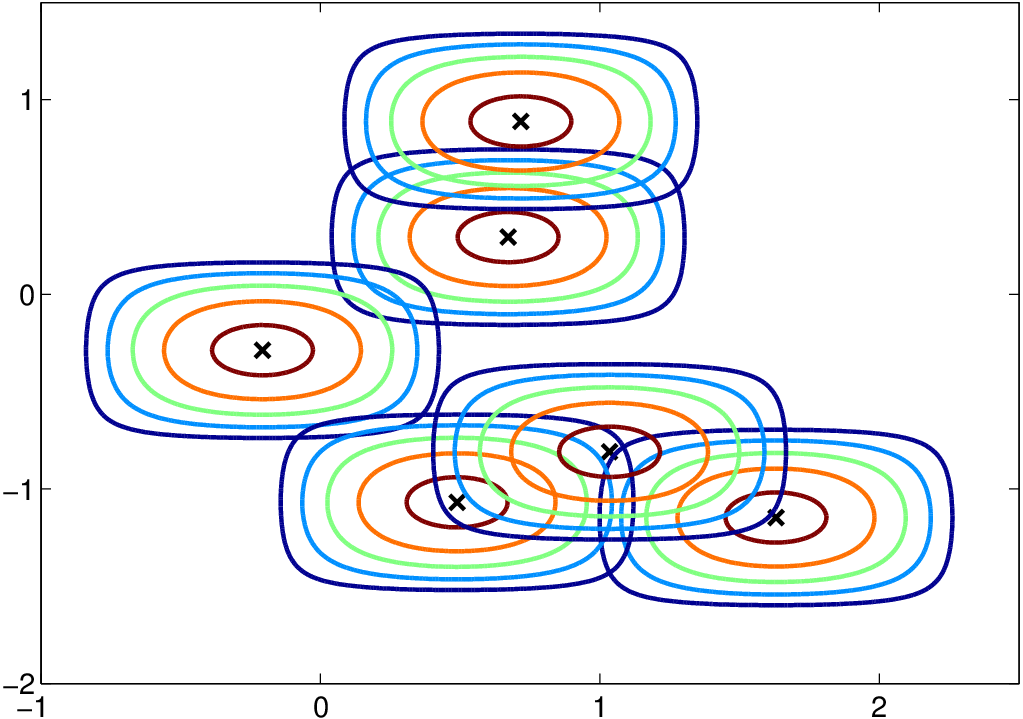
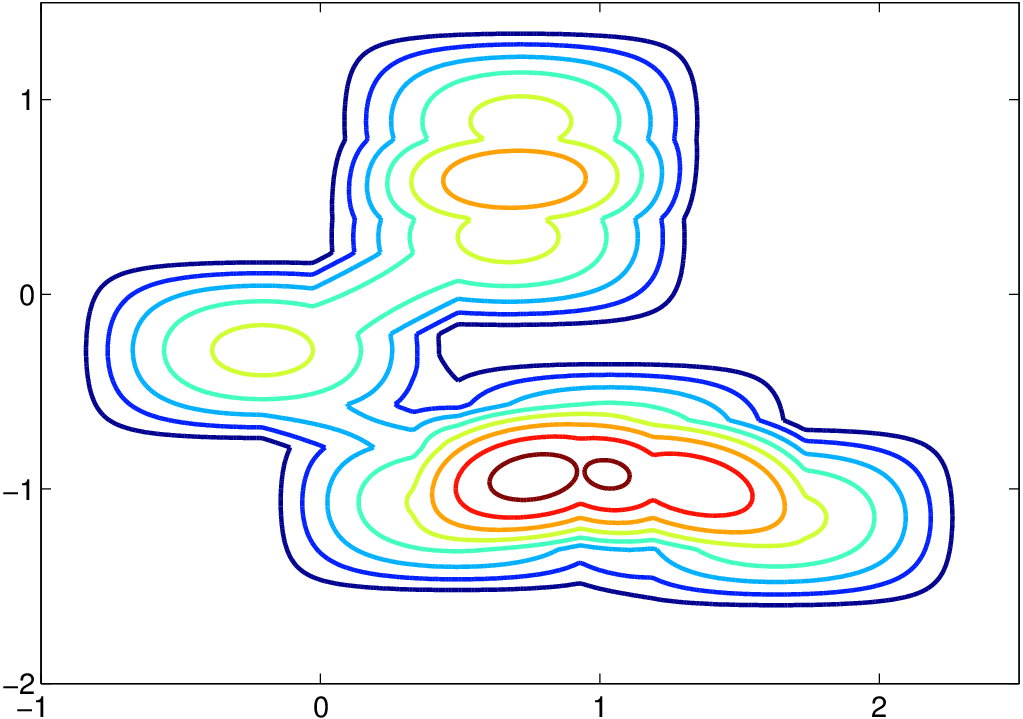
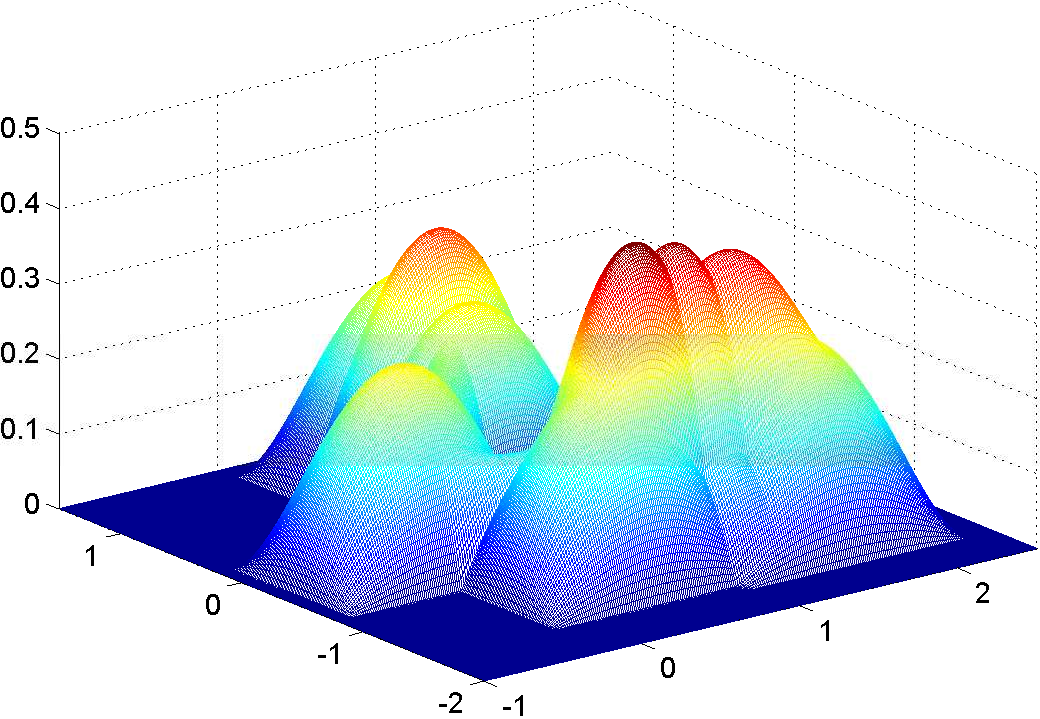
Konstrukce jádrového odhadu je analogická konstrukci jednorozměrného odhadu. Tedy v každém bodě sestrojíme jádro a odhad v bodě je průměr hodnot jader v tomto bodě - viz následující obrázek.

Obr. 4. Konstrukce jádrového odhadu hustoty

¹Používáme zde zkrácený zápis pro dvourozměrnou hustotu normálního rozdělení, a to