Iterační metoda

V tomto odstavci pojednáme o další metodě pro odhad vyhlazovacího parametru. Metodu pouze popíšeme a nebudeme se zabývat statistickými vlastnostmi získané aproximace. Podrobnou analýzu lze najít v monografii [3]. Tato metoda je založena na vztahu Jádrové odhady hustoty (7):

Přepíšeme tuto rovnici

(19)

Problém nalézt pro které nabývá minimální hodnoty, je tedy ekvivalentní řešení této rovnice. Zde se ovšem vyskytuje stejný problém - neznáme hodnotu a proto budeme počítat s odhady rozptylu a vychýlení. Tyto odhady uvažujeme ve tvaru

Odtud plyne

(20)

a

Výraz lze upravit pomocí konvolucí a dostaneme

Funkce má tyto vlastnosti

		(21)

je vychýleným odhadem AISB, a proto budeme uvažovat

(22)

Místo rovnice Jádrové odhady hustoty (19) řešíme rovnici

Rovnici lze také zapsat ve tvaru:

(23)

Uvedenou rovnici lze řešit Newtonovou metodou, neboť derivaci funkce lze snadno spočítat užitím konvolucí. Řešení této rovnice označíme

Řešení rovnice Jádrové odhady hustoty (23) lze považovat za vhodnou aproximaci Tato skutečnost je dokázána v následující větě [3].

Věta 5.11. Nechť

a

Pak platí

Poznámka 3.12. Rychlost konvergence pro metodu křížového ověřování:

Rychlost konvergence pro iterační metodu

Řády rychlosti konvergence pro CV metodu a iterační metodu jsou stejné, ale výhodou iterační metody je podstatně menší výpočetní náročnost.

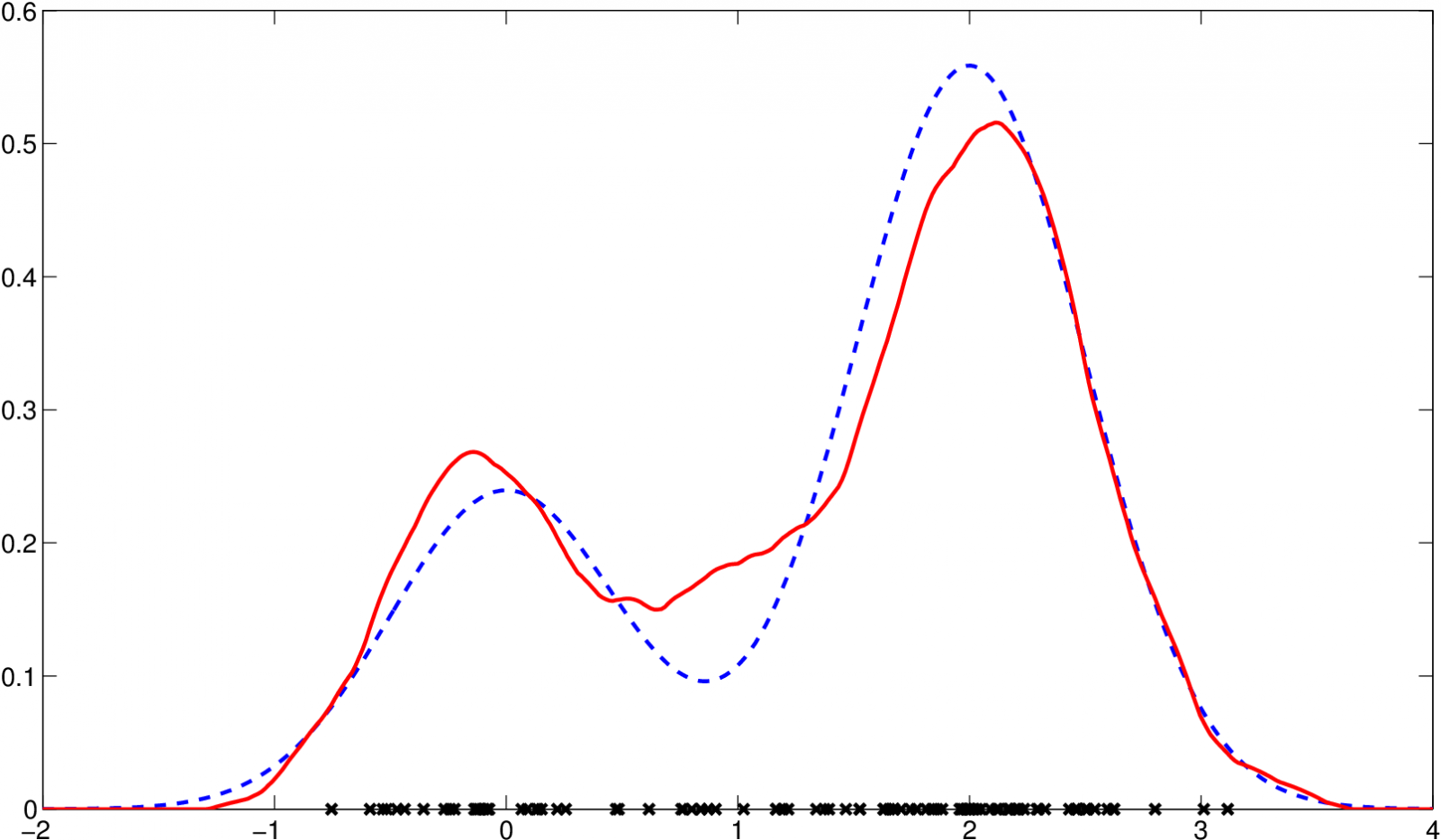
Příklad 3.13. Jádrový odhad hustoty dat z příkladu Jádrové odhady hustoty 2.1 s Epanečnikovým jádrem a vyhlazovacím parametrem určeným iterační metodou je uveden na obrázku:

Obr. 12. Odhad hustoty s hIT =0,5314, odhad (červená, plná), původní funkce (modrá, čárkovaná)