Simulace Poissonova procesu

Simulace, též nazývaná Monte-Carlo experiment, je důležitou součástí matematického modelování, neboť umožňuje studium těch matematických modelů, pro které neexistují analytické výsledky a umožňuje ilustraci ve formě experimentálních dat, avšak se známými vlastnostmi.

Využijeme přitom toho, že časové intervaly mezi po sobě jdoucími událostmi , jsou nsr s exponenciálním rozdělením s parametrem , tvoří tedy náhodný výběr z tohoto rozdělení. Samotná simulace Poissonova procesu pak spočívá ve vygenerování náhodného vzorku intervalů mezi událostmi, a výpočtu okamžiků jednotlivých událostí_, . Hodnota Poissonova procesu je pak v těchto bodech rovna

v intervalech mezi těmito body funkci doplníme tak, aby byla po částech konstatní zprava spojitá a aby pro Dostáváme jednu trajektorii Poissonova procesu.

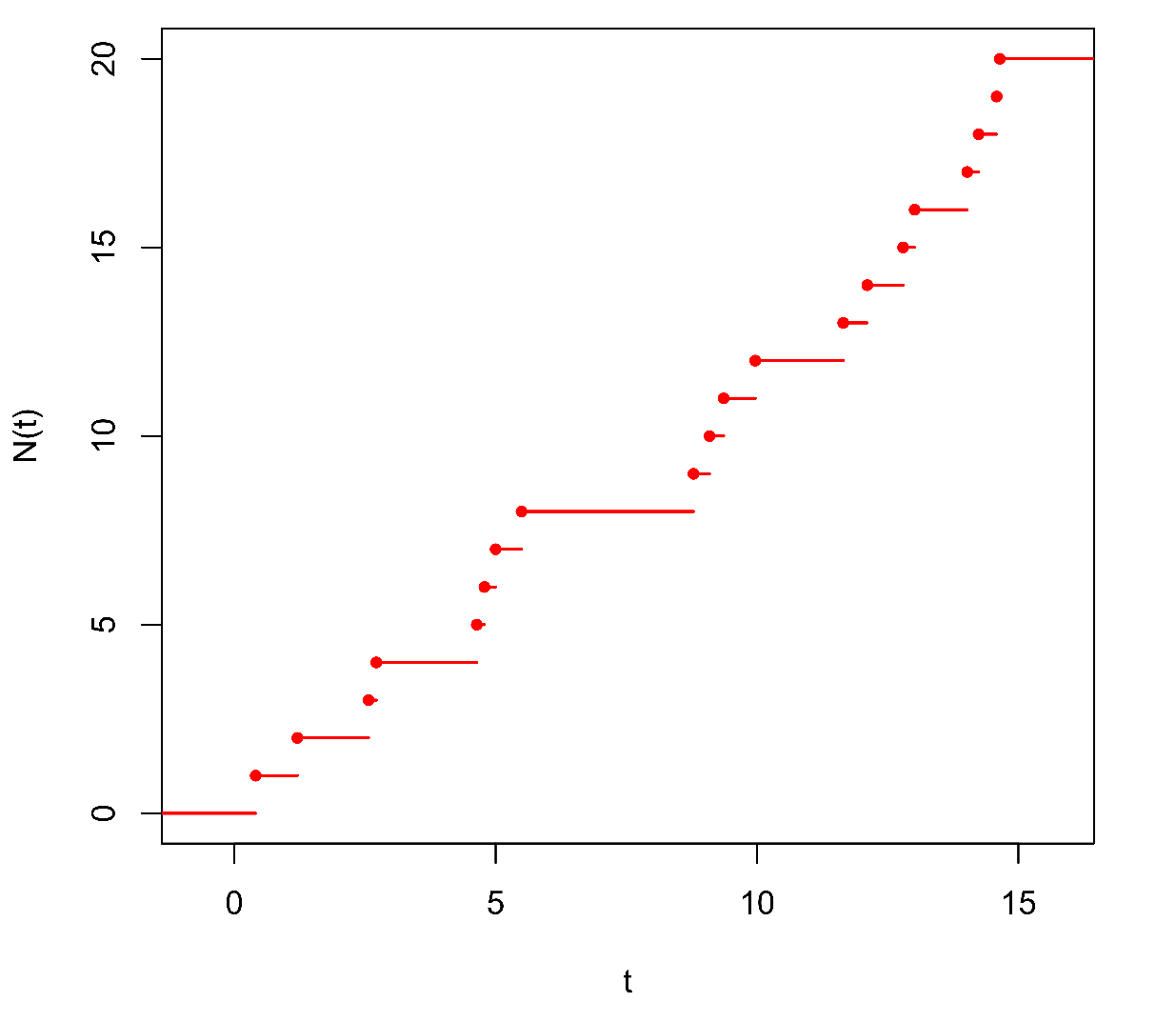
Nyní podáme praktický návod, jak vygenerovat takovou trajektorii ve statistickém softwaru R [2]. Pro základní práci v R odkazujeme na příslušnou část textu Výpočetní matematické systémy. Nejdříve si do proměnné K uložíme počet generovaných okamžiků událostí a do proměnné lambda hodnotu intenzity . Poté pomocí funkce rexp generujeme náhodný výběr z exponenciálního rozdělení se zadanou intenzitou. V níže uvedeném kódu je tento vzorek nasimulovaných časů mezi příchody událostí uložen do proměnné T. Okamžiky událostí, S, spočítáme pomocí kumulativního součtu příkazem cumsum. Do proměnné N, reprezentující hodnotu Poissonova procesu v časech S, uložíme posloupnost přirozených čísel. Přitom přidáme hodnotu 0  na počátek N, takže délka vektoru N je o jedničku větší než délka vektoru S. Trajektorii X Poissonova procesu pak vytvoříme příkazem stepfun jako tzv. schodovitou funkci (step function) interpolující zadané body.

Získanou trajektorii můžeme vykreslit do obrázku.

K <- 20
lambda <- 1.5
T <- rexp (K, rate=lambda)
S <- cumsum (T)
N <- seq (0, length(S), by=1)
X <- stepfun (S, N)
plot (X, verticals=FALSE, pch=20, col=2, lwd=1.5,
xlab="t", ylab="N(t)", main="")

Obr.1 ukazuje dvě trajektorie Poissonova procesu se intenzitou .

Obr.1: Dvě trajektorie Poissonova procesu s intenzitou . Hodnota procesu udává počet zaznamenaných událostí do času včetně. Čas každého skoku v grafu trajektorie odpovídá okamžiku jedné události.