Binomické a Poissonovo rozdělení pravděpodobnosti

Bernoulliovským pokusem (alternativním pokusem) v teorii pravděpodobnosti a statistice rozumíme náhodný pokus, který má právě dva možné výsledky, obvykle nazývané úspěch a neúspěch.  Úspěchem pak rozumíme tu možnost, která je podstatou našeho sledování. Podle zaměření experimentu tak úspěchem může být např. padnutí šestky při hodu kostkou, výhra v loterii, silnější list v karetní hře, uzdravení pacienta (v biomedicínských aplikacích),ale též úmrtí jedince (v analýze přežití), porucha stroje (v teorii spolehlivosti), havárie automobilu (v pojišťovnictví), výbuch sopky či jiná přírodní katastrofa. Pravděpodobnost, že nastane úspěch, budeme označovat , pravděpodobnost neúspěchu je pak rovna .

Předpokládejme, že posloupnost bernoulliovských pokusů provádíme  n krát po sobě, přičemž jednotlivá opakování jsou nezávislá. Označme diskrétní náhodnou veličinu, udávající, kolikrát v posloupnosti pokusů nastal úspěch. Veličina tedy může nabýt hodnot a její rozdělení pravděpodobnosti je známé jako binomické rozdělení. Jeho pravděpodobnostní funkce (probability mass function) je rovna

(1)

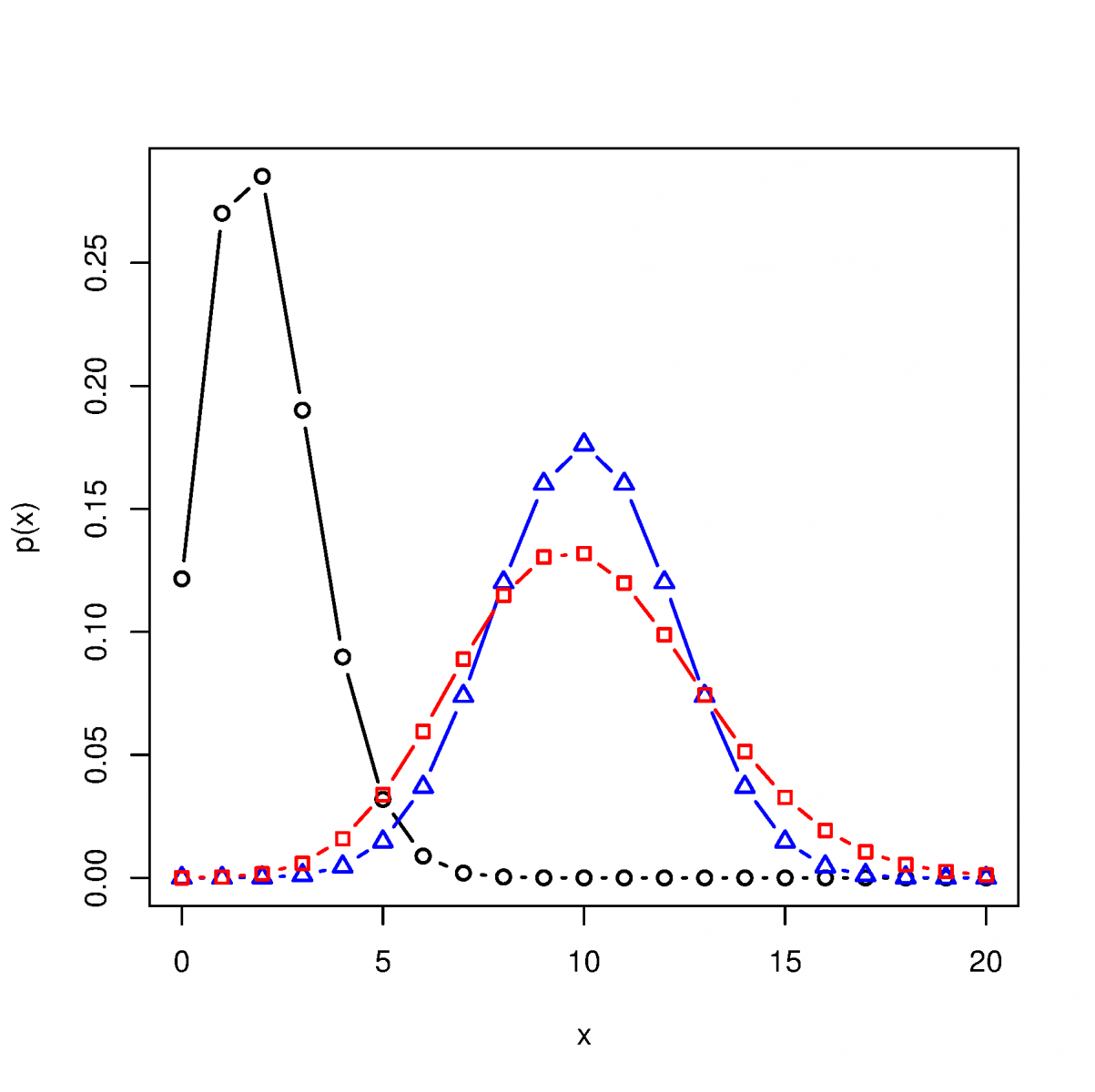
Grafy pravděpodobnostní funkce (1) a odpovídající distribuční funkce (cumulative distribution function) jsou pro některé hodnoty parametrů zobrazeny na Obr. 1. Známými skutečnostmi jsou vztahy pro střední hodnotu a rozptyl binomické náhodné veličiny:

(2)

(3)

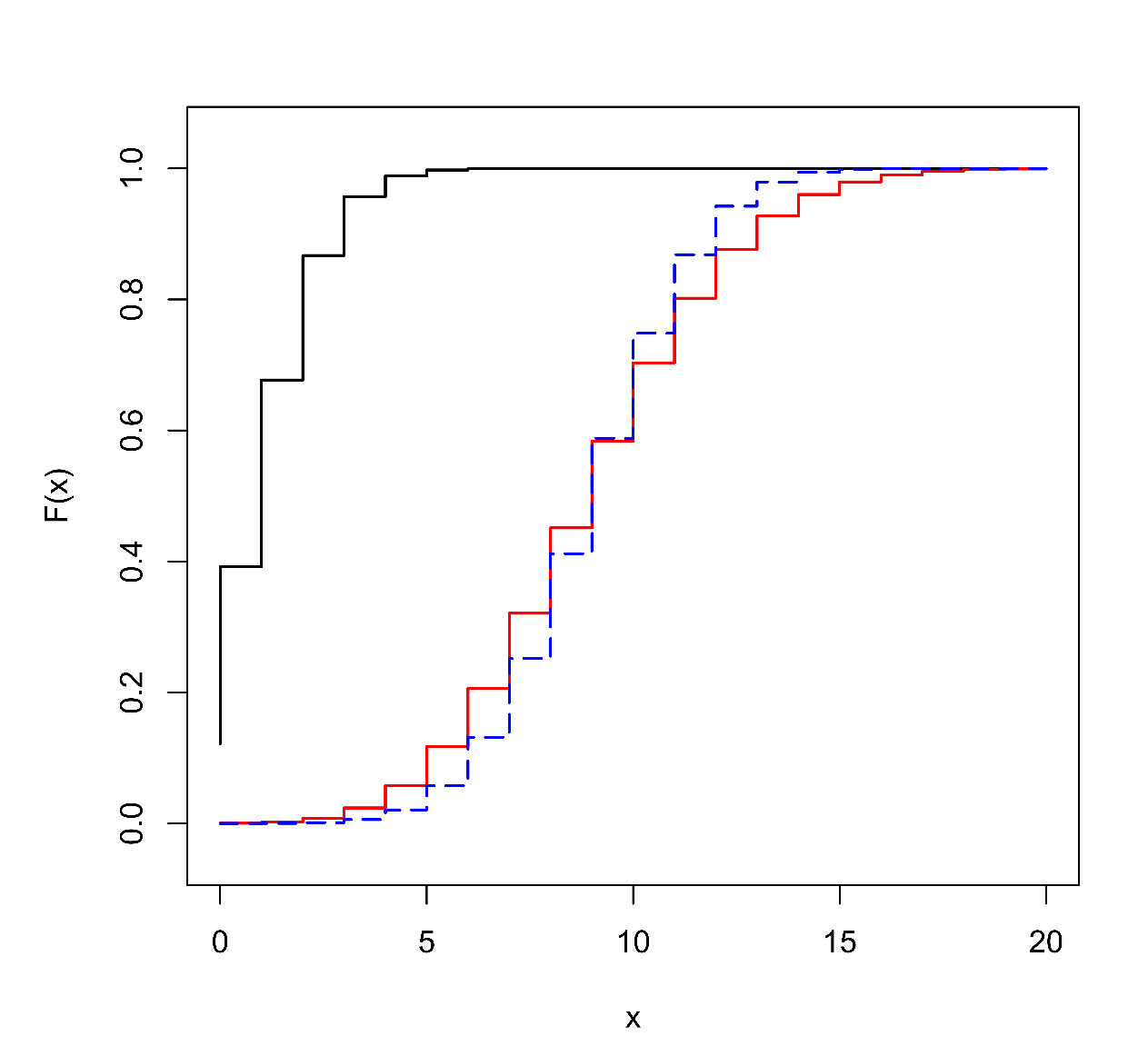Obr. 1: Pravděpodobnostní funkce a odpovídající distribuční funkce binomického rozdělení pravděpodobnosti s parametry (černě, kolečka), (červeně, čtverečky) a  (modře, trojúhelníčky).

Pokud je počet opakování bernoulliovského pokusu s malou pravděpodobností úspěchu velmi velký, přičemž součin zůstává konečný a nenulový, binomické rozdělení se asymptoticky blíží k tzv. Poissonovu rozdělení pravděpodobnosti. Nechť náhodná veličina nabývá hodnot  , a to s pravděpodobnostmi

(4)

kde je daný konstantní parametr. Potom říkáme, že náhodná veličina má Poissonovo rozdělení pravděpodobnosti s parametrem . Někdy je nazýváno též. zákonem malých čísel, neboť se jedná o statistický popis výskytu událostí, které se vyskytují zřídka, mají však mnoho příležitostí nastat. Za určitých podmínek, které budou specifikovány později, taková náhodná veličina udává počet událostí, které nastanou v časovém intervalu jednotkové délky. Jak v takovém případě uvidíme, parametr udává střední počet událostí za jednotku času, jeho rozměr je tedy převrácenou hodnotou jednotky času. 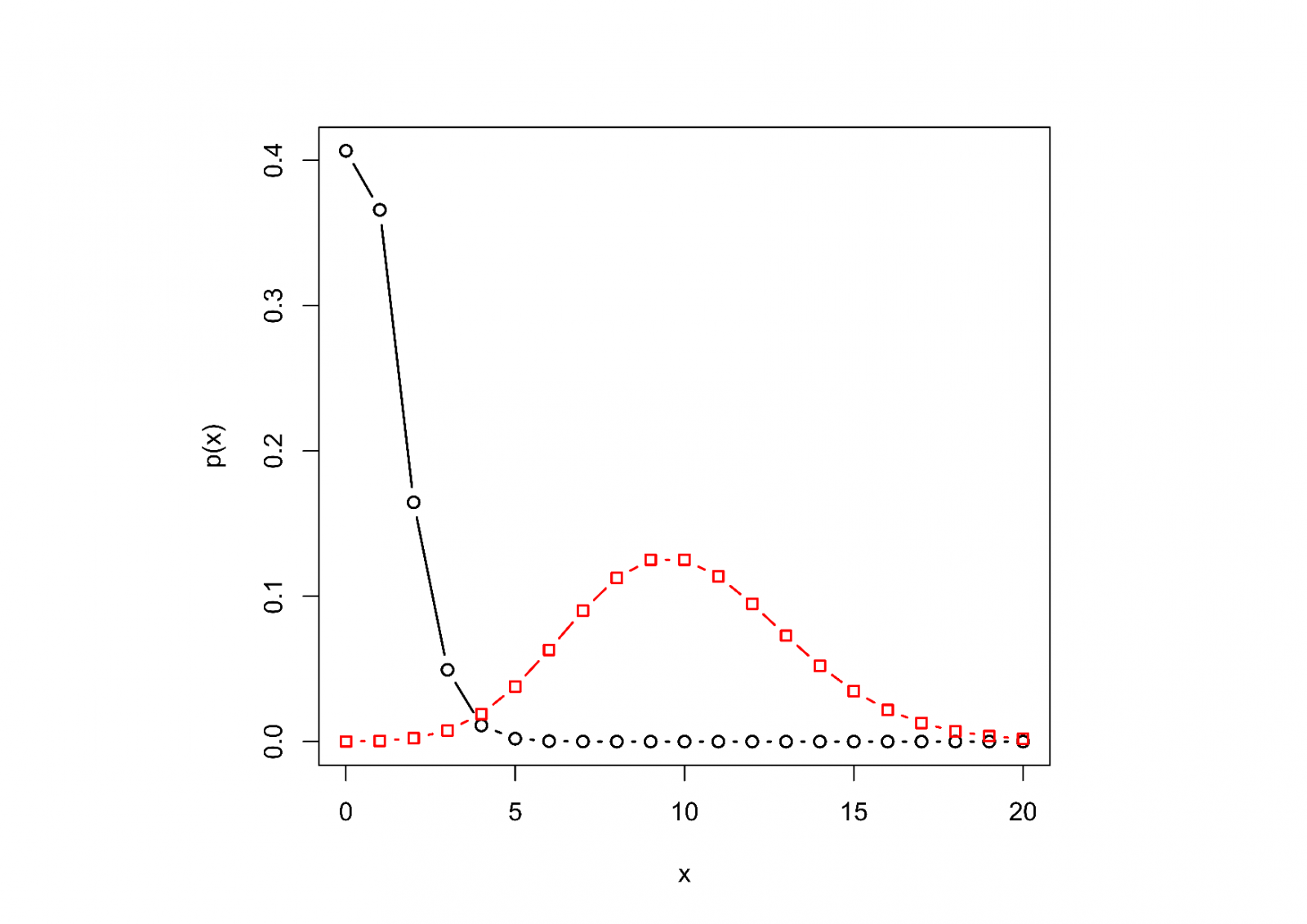Grafy funkce a odpovídající distribuční funkce jsou pro některé hodnoty parametru zobrazeny na Obr. 2.

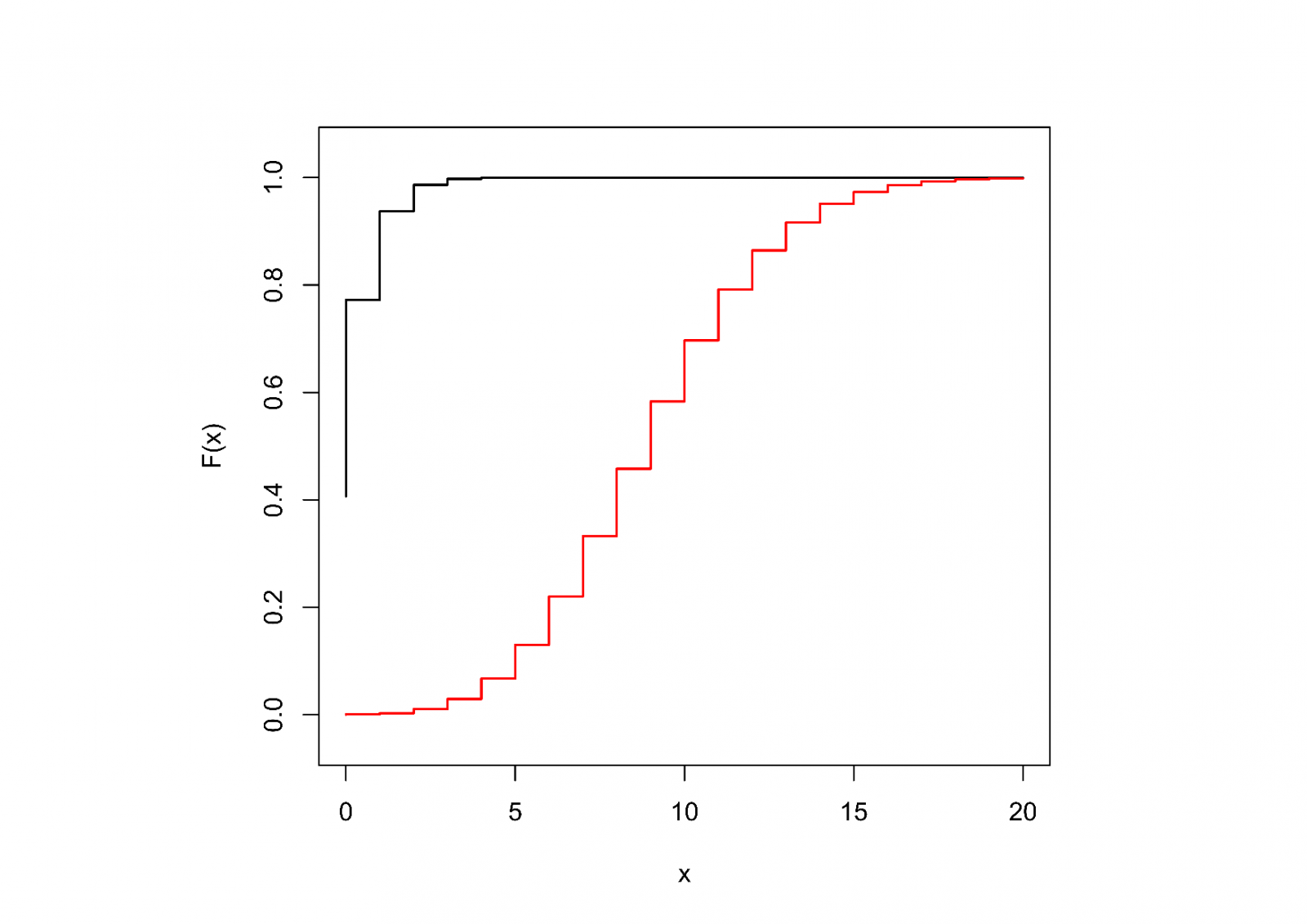Obr. 2: Pravděpodobnostní funkce a odpovídající distribuční funkce Poissonova rozdělení pravděpodobnosti s parametry (černě, kolečka) a   (červeně, čtverěcky). Povšimněme si, že  pro velké je tvar pravděpodobnostní funkce podobný hustotě normálního (Gaussova) rozdělení.

Odvození střední hodnoty a rozptylu poissonovské náhodné veličiny ponecháváme jako cvičení pro čtenáře. Výsledná rovnost

(5)

je typickým poznávacím znamením Poissonova rozdělení pravděpodobnosti. Odtud lze jednoduše získat momentový odhad parametru   Známe-li realizaci náhodného výběru , střední hodnotu aproximujeme výběrovým průměrem a dostáváme momentový odhad ve tvaru

(6)

Lze ověřit, že tento odhad je také maximálně věrohodným odhadem.

Příklad (Úmrtí následkem kopnutí koněm)

V roce 1898 publikoval Ladislaus von Bortkiewicz práci s názvem Das Gesetz der kleinen Zahlen, kde uvedl tabulku počtu úmrtí vojáků 10 pruských kavalerií v důsledku kopnutí koněm v letech 1875 až 1894, viz první dva sloupce v Tab. 1. Druhý sloupec udává, kolikrát bylo v jedné kavalerii během jednoho roku zaznamenáno 0 až 4 úmrtí, 5 či více úmrtí nenastalo.

Tab. 1: Počty vojáků 10 pruských kavalerií, kteří zemřeli po koňském kopnutí za dobu 20 let (1875-1894); podle [3].

počet úmrtí v kavalerii za jeden rok	pozorované četnosti,	teoretické četnosti,
0	109	108.7
1	65	66.3
2	22	20.2
3	3	4.1
4	1	0.6
5+	0	0.1
celkem,	200	200.0

Nejprve za předpokladu poissonovského rozdělení pravděpodobnosti odhadneme parametr . Dosadíme do (6) a dostáváme

K ověření toho, že zaznamenané počty úmrtí odpovídají Poissonovu rozdělení, nyní provedeme test dobré shody. Čtenáře, neznalého této metody, odkazujeme např. na knihu Anděl (2005). Testovací statistika má tvar

kde je celkový počet pozorování, jsou třídy pozorování a počty pozorování v nich (tzv. empirické četnosti). Hodnoty jsou pak teoretické relativní četnosti, tzn. odhadnuté pravděpodobnosti. V našem případě je

Pozorované četnosti jsou uvedeny ve druhém sloupci Tab. 1, spočítané teoretické četnosti jsou pak uvedeny ve třetím sloupci. Všimněme si, jak jsou si pozorované a teoretické četnosti blízké.

Dosazením do testovací statistiky dostáváme její hodnotu . Tu porovnáme s 95% kvantilem rozdělení pravděpodobnosti, přičemž počet stupňů volnosti je roven počtu tříd zmenšenému o dvě. Počet četnosti totiž dále snižujeme o jedničku za každý parametr, který jsme odhadli (v našem případě ). Příslušný kvantil je rovný . Hodnota testovací statistiky je hluboko pod touto hodnotou, na hladině významnosti 5% tedy nezamítáme naši hypotézu, že tato poněkud bizarní data mají Poissonovo rozdělení pravděpodobnosti. Na druhou stranu lze očekávat, že úmrtí v důsledku kopnutí koněm bude vzácným jevem a počty těchto událostí se tak budou řídit zákonem malých čísel.