Proces ryzího zániku

Významově opačným modelem, tedy pro modelem vymírání populace, je proces ryzího zániku (pure death process).
Ten je, podobně jako Yuleův proces, definován následujícími vlastnostmi.
Na začátku pozorování je velikost populace rovna .
Každý jedinec, živý v čase má pravděpodobnost úmrtí v časovém intervalu rovnu .
Dále předpokládáme, že úmrtí jednotlivých jedinců jsou na sobě nezávislá, a že pravděpodobnost úmrtí více než jednoho jedince během intervalu je pro malé  rovna .
Opět chceme určit pravděpodobnostní rozdělení velikosti populace v čase, zadané pravděpodobnostními funkcemi pro a .

Začneme případem , tedy že v populace je jen jeden jedinec.
Číslo , resp. , vyjadřuje pravděpodobnost, že tento jedinec je v čase , resp. , ještě živý. V definici procesu je určeno, že pravděpodobnost přežití časového intervalu  je pro každého jedince rovna , a pomocí pravidla o násobení pravděpodobností tak dostáváme vztah

(11)

Limitním přechodem dospějeme k diferenciální rovnici

(12)

s počáteční podmínkou . Řešením této počáteční úlohy je funkce

(13)

Obecně, když populace má na počítku velikost ,
počet přeživších jedinců v čase je náhodnou veličinou s binomickým rozdělením s parametry a .
"Úspěchy" tu představují úmrtí jedinců, a ta jsou dle definice procesu nezávislá.
Podle (Zákon malých čísel 1) tak dostáváme pravděpodobnostní funkci velikosti populace v čase ,

(14)

a střední hodnotu a rozptyl velikosti populace,

	(15)
	(16)

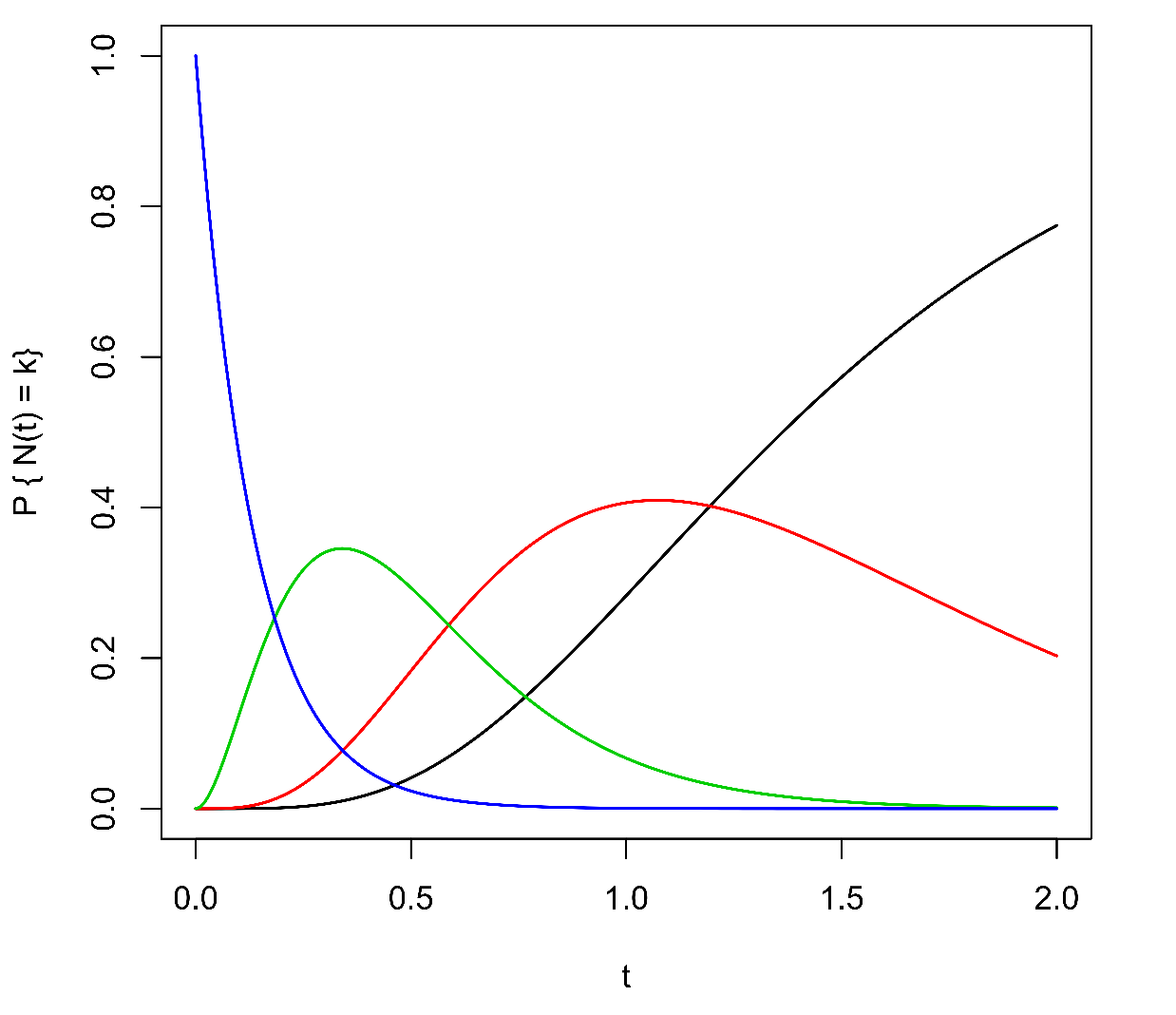
Obr. 2: Vlevo: pravděpodobnostní funkce (14) procesu ryzího zániku jako funkce času, , pro velikosti populace
 k = 0 (černě), ( 1 ) (červeně), ( 3 ) (zeleně) a  (modře).
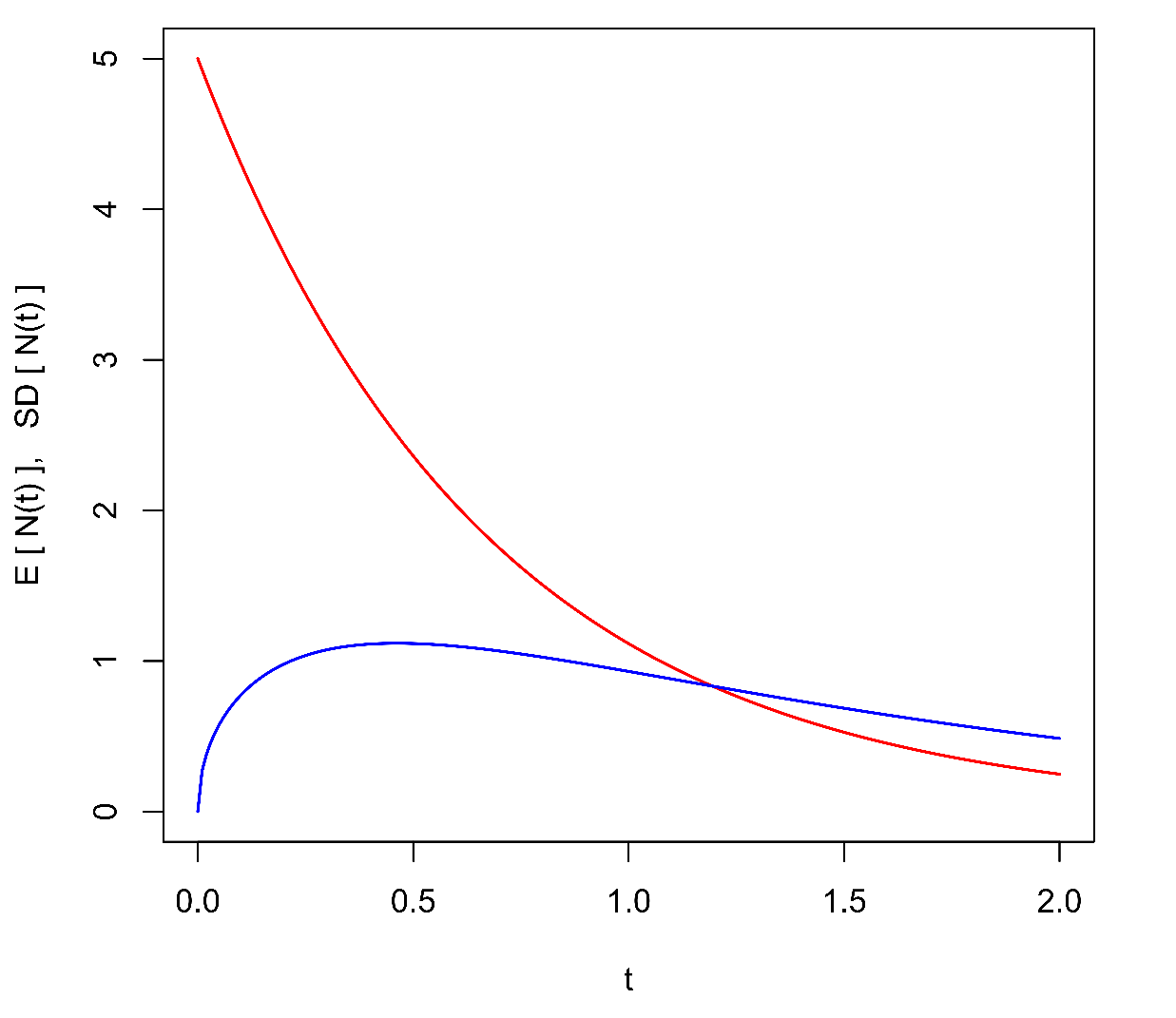
Vpravo: střední hodnota (červeně) a směrodatná odchylka (modře) velikosti populace v čase.
Parametr , počáteční velikost populace byla .

Grafy pravděpodobnostních funkcí (14) pro některá v závislosti na čase jsou nakresleny na Obr. 2 vlevo.
Pro pravděpodobnostní funkce exponenciálně klesá z hodnoty 1 k nule,
pro  funkce začínají v bodě 0, nabývají lokálních maxim v časech  a poté klesají k nule,
a pro  funkce roste z nuly do asymptotické hodnoty jedna.
Průbehy střední hodnoty (15) a směrodatné odchylky (odmocniny z (16)) jsou nakresleny na Obr. 2 vpravo.
Střední hodnota exponenciálně klesá, zatímco rozptyl nabývá lokálního maxima v čase .

V procesu ryzího zániku se velikost populace buď nemění, anebo klesá. Když dosáhne hodnoty nula, říkáme, že populace vyhynula. Pravděpodobnost, že populace je vyhynulá v čase (tzn. vyhynula nejpozději v čase ) je

(17)

Pro tato pravděpodobnost konverguje k jedné, populace tedy zřejmě nevyhnutelně vyhyne.