Od Bernoulliho k Poissonovi

Tuto podkapitolu věnujeme odvození Poissonova rozdělení pravděpodobnosti z binomického rozdělení. Bude se sice jednat o ryze matematický text, pro čtenáře by však měl být spíše osvěžením znalostí z matematické analýzy, na níž právě teorie pravděpodobnosti a matematická statistika staví své základy.
Vyjdeme z pravděpodobnostní funkce (1) binomického rozdělení a budeme uvažovat limitní přechod

Vyjádříme , čímž eliminujeme limitní přechod , a dosadíme do vyjádření pravděpodobnostní funkce:

Výraz rozdělíme na tři části,

jejichž limity pro spočítáme samostatně. Limita první části je zřejmá,

Pro výpočet limity druhého členu využijeme asymptotického vyjádření exponenciální funkce:

(7)

S její pomocí dostáváme

Pro výpočet limity třetího členu využijeme tzv. Stirlingovu aproximaci ([1]) faktoriálu:
 

pro velká N.

(8)

Tu použijeme pro přepsání faktoriálů a a postupnými úpravami výrazu dostáváme:

Samostatně spočítáme limity jednotlivých umocněných závorek. Zřejmé jsou limity

Při výpočtu limity

pak opět využijeme limitního tvaru exponenciální funkce. Celkově dostáváme limitu členu ve tvaru .

Limita pravděpodobnostní funkce binomického rozdělení je tedy rovna

což je pravděpodobnostní funkce (4) Poissonova rozdělení.
Graficky je porovnání pravděpodobnostních funkcí binomického rozdělení s parametry a Poissonova rozdělení s parametrem ukázáno na Obr.3.
Všimněme si, že Poissonova rozdělení podhodnocuje pravděpodobnosti kolem střední hodnoty a nadhodnocuje pravděpodobnosti pro velká .

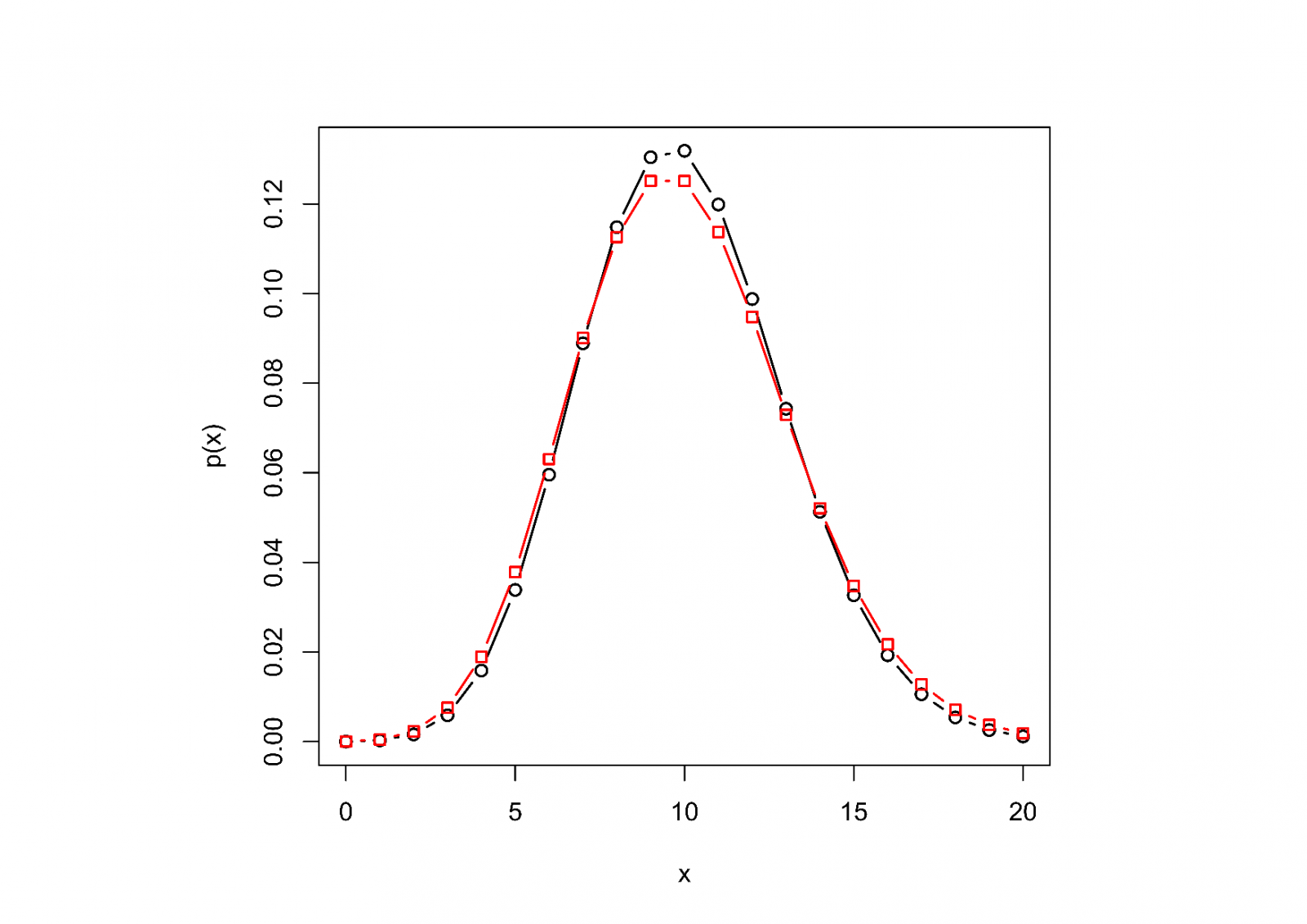Obr. 3: Porovnání pravděpodobnostních funkcí binomického rozdělení s (černá kolečka) a Poissonova rozdělení s (červené čtverečky).

Poznámka (Asymptotické vyjádření exponenciální funkce)

Platnost vztahu (7), kterého často využíváme při odvozování limitních rozdělení pravděpodobnosti, nemusí být na první pohled jasná. Rozepišme proto výraz uvnitř limity podle binomické věty. Postupnými úpravami dostáváme: 

Limitním přechodem sice naroste počet členů řady, ale odpadnou výrazy v závorkách, neboť všechny konvergují k jedničce. Dostaneme tak řadu 

o níž je známo (přesvědčíme se přímým výpočtem), že jde o Taylorovu řadu exponenciální funkce rozvinutou v bodě nula.