Jednoduchá náhodná procházka

Náhodná procházka je základním modelem časového vývoje veličin, které nabývají celočíselných hodnot -např. po zaokrouhlení či vyjádření ve vhodných jednotkách -, a to v mnoha oblastech vědy, mj. ve fyzice, ekologii, psychologii i ekonomii. V literatuře je popsáno mnoho jejích různých variant, zde se zaměříme jen na některé z nich a popíšeme jejich vlastnosti. Využijeme přitom literaturu [2, 4, 5].

Při výkladu použijeme fyzikální reprezentaci pomocí popisu polohy částice (hodnota náhodné procházky) v čase. Předpokládejme, že částice, jejíž pohyb sledujeme, se v čase 0 nachází v nulové poloze. Od tohoto okamžiku je pak v každém časovém kroku její poloha o jednotku zvýšena nebo snížena, v závislosti na výsledku alternativního (bernoulliovského) pokusu s danou konstantní pravděpodobností úspěchu . Dále předpokládáme, že prováděné alternativní pokusy jsou navzájem nezávislé.

Označme polohu objektu po krocích symbolem . Formálně je tzv. jednoduchá náhodná procházka (simple random walk) definována následujícími vlastnostmi:

(i)	, tj. proces začíná s pravděpodobností 1 v bodě 0,
(ii)	kde jsou nsr náhodné veličiny s diskrétním (dvoubodovým) rozdělením pravděpodobnosti

(1)

Podmínku (ii)je možno ekvivalentně zapsat také ve tvaru

(iii)

Náhodná procházka je markovským procesem s diskrétními stavy a diskrétním časem.

Hodnota , kterou proces nabývá v čase totiž dle (ii) závisí pouze na jeho hodnotě v předchozím časovém okamžiku, , nikoliv na trajektorii, která jej do tohoto stavu dovedla. V případě, že pravděpodobnosti úspěchu a neúspěchu v alternativních pokusech jsou stejné, tedy , nazýváme výsledný proces symetrickou náhodnou procházkou.

Vygenerovat trajektorii náhodné procházky není obtížné. Následující příkazy ukazují provedení takového Monte-Carlo experimentu v prostředí R [3]. Předpokládáme přitom, že čtenář se již seznámil se simulací z části SMPp.1.

K <- 50
p <- 0.6
N <- seq (0, K)
Z <- 2 * rbinom (K, 1, p) - 1
X <- c (0, cumsum (Z))
plot (N, X, type="b", pch=16, col=2, xlab="n", ylab="X_n")

Za zmínku stojí čtvrtý řádek, kde pro získání náhodného výběru Z z rozdělení (1) používáme příkaz rbinom pro vzorek z binomického rozdělení (Zákon malých čísel 1)., které při nastavení druhého parametru na 1 odpovídá alternativnímu rozdělení. Protože takový vzorek obsahuje jen nuly a jedničky, na požadované hodnoty jej ještě musíme transformovat.

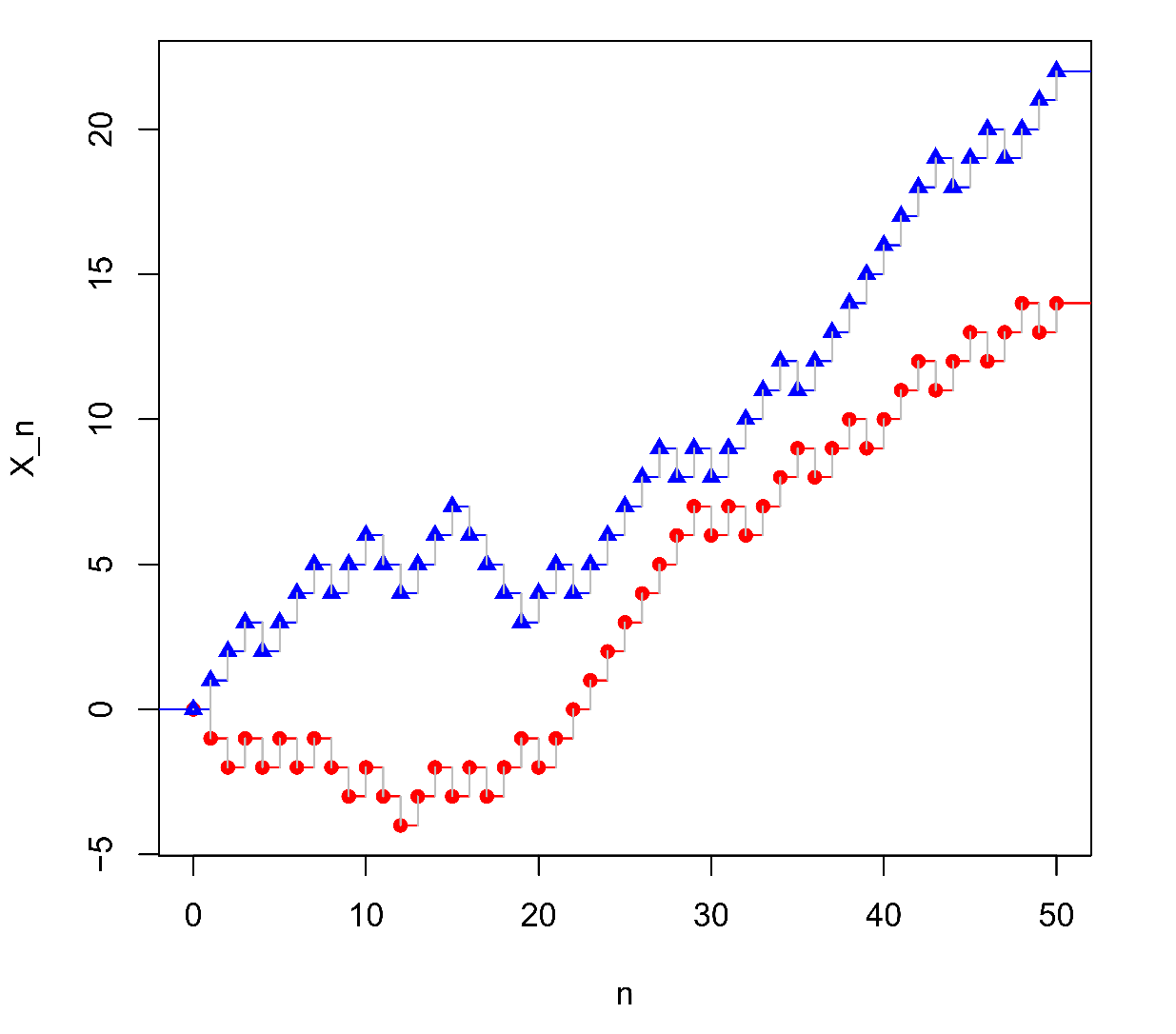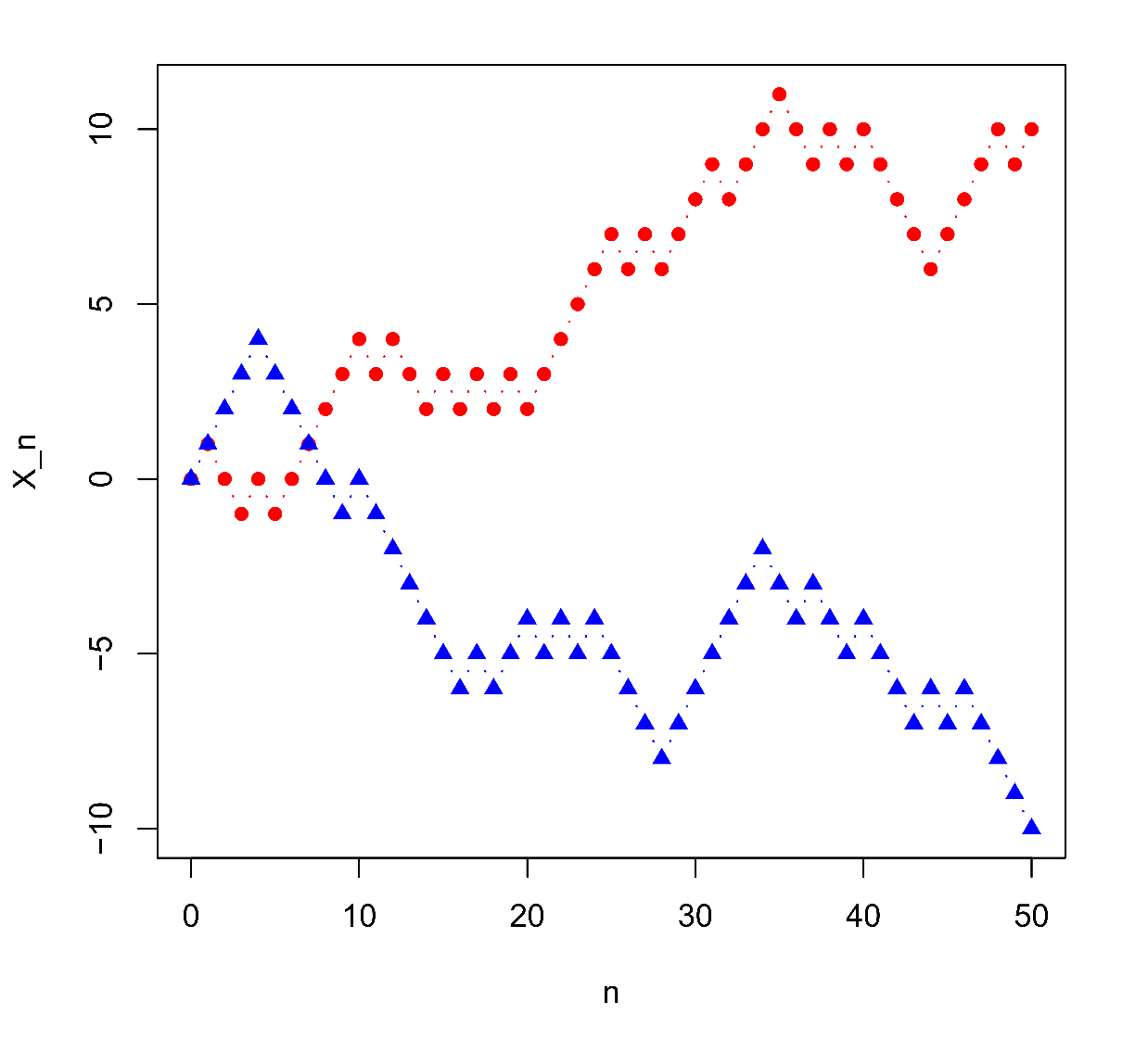
Obr.1:Vlevo dvě trajektorie symetrické náhodné procházky, vpravo dvě trajektorie jednoduché náhodné procházky s p = 0,6.

Několik typických trajektorií náhodných procházek je nakresleno v Obr.1. Obvykle se kreslí jen body odpovídající hodnotám procesu (graf vlevo), lze se však setkat i se znázorněním pomocí schodovité funkce (graf vpravo) jakoby procesu se spojitým časem.