Slovník | Vyhledávání | Mapa webu
 
Analýza a modelování dynamických biologických datVybrané kapitoly z matematického modelování Procesy větvení Číselné charakteristiky
Logo Matematická biologie

Číselné charakteristiky

Protože podle (ii) jsou náhodné veličiny nsr, mají také stejné číselné charakteristiky. Označme střední počet potomků každého jedince (v libovolné generaci)

(3)

a rozptyl počtu potomků

(4)

Pro odvození střední hodnoty počtu jedinců v -ní generaci vyjdeme z (2), kde náhodný součet rozepíšeme podle vzorce pro úplnou pravděpodobnost,

Střední hodnota v uvedeném výrazu je přitom rovna , neboť jde vlastně o sumu středních hodnot počtu potomků jedinců. Dosazením a úpravou tak dostáváme rekurzivní vztah (pro )

(5)

Z (i) a (1) přitom máme , explicitní tvar pro střední hodnotu velikosti populace je tedy rovný

(6)

Nyní odvodíme rozptyl velikosti populace v -té generaci. Jak již bylo řečeno, náhodné veličiny jsou nsr a platí tedy 

Tohoto vztahu a (6) využijeme při výpočtu podmíněného druhého momentu,

E ( X n + 1 2 | X n = k ) = Var ( X n + 1 | X n = k ) + [ E ( X n + 1 2 | X n = k ) ] 2 = k σ 2 + k 2 μ 2 .

Využitím vzorce pro úplnou pravděpodobnost pak počítáme

E ( X n + 1 2 ) = ∑ k = 0 ∞ P { X n = k } E ( X n + 1 2 | X n = k ) = ∑ k = 0 ∞ ( k σ 2 + k 2 μ 2 ) P { X n = k } =
= σ 2 ∑ k = 0 ∞ k P { X n = k } + μ 2 ∑ k = 0 ∞ k 2 P { X n = k } = σ 2 E ( X n ) + μ 2 E ( X n 2 ) .

Dosadíme z (6) a vyjádříme rozptyl velikosti populace,

čímž obdržíme rekurentní vztah

(7)

Z podmínky (i) máme , jako cvičení pro čtenáře pak ponecháváme vyjádření explicitního vztahu pro rozptyl velikosti populace

(8)

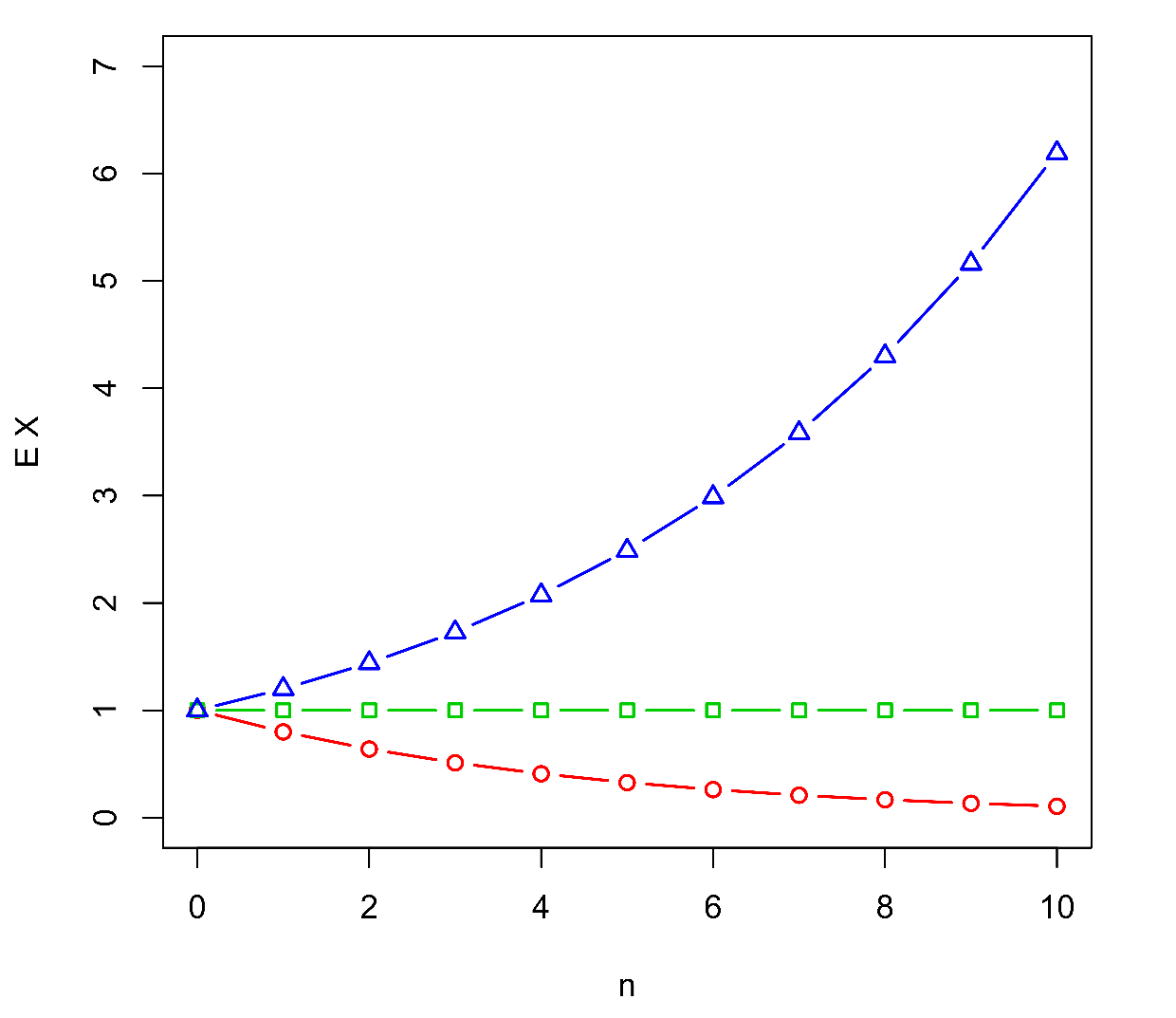
Grafy průběhů střední hodnoty (6) a rozptylu (8) v závislosti na generaci jsou pro různé hodnoty střední hodnoty počtu potomků, , vykresleny na (Obr.2.

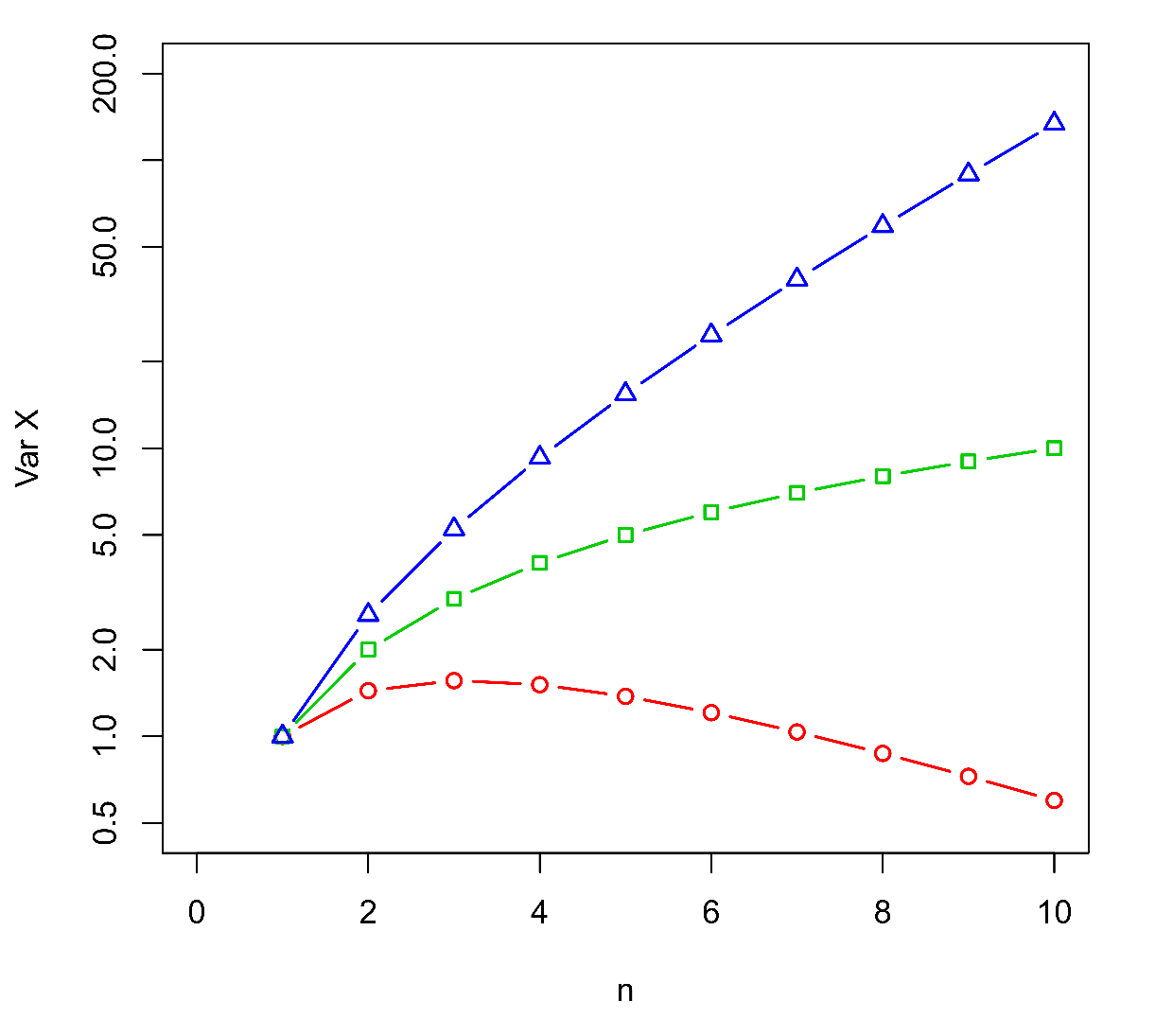Obr.2: Střední hodnota, , a rozptyl, , velikosti populace Galtonova-Watsonova procesu větvení v závislosti na generaci, . Hodnoty rozptylu (graf vpravo) jsou uvedeny na logaritmické škále. Parametry: (červeně, kolečka), (zeleně, čtverečky), (modře, trojúhelníky); .

Všimněme si asymptotického chování () střední hodnoty a rozptylu velikosti populace. Při obě charakteristiky konvergují k nule, při obě divergují. Zajímavý je případ , kdy je v populaci v průměru stále jen jeden jedinec, ale rozptyl velikosti populace roste nade všechny meze.

 

 

 
vytvořil Institut biostatistiky a analýz Lékařské fakulty Masarykovy univerzity