Nehomogenní Poissonův proces

Jedním z omezení (homogenního) Poissonova procesu je konstantní hodnota intenzity v předpokladech (i) a (ii) . Změníme-li tyto předpoklady na

(i*)
(ii*)

kde , , je po částech spojitá nezáporná funkce, obdržíme nehomogenní Poissonův proces, neboli Poissonův proces s proměnnou intenzitou .
Pro nehomogenní Poissonův proces lze analogickým způsobem jako pro homogenní variantu odvodit rozdělení pravděpodobnosti počtu událostí v časovém intervalu . Odpovídající pravděpodobnostní funkce je tvaru

(1)

Pro počet událostí od počátku sledování, , dostáváme

(2)

tzn. počet událostí je náhodnou veličinou s Poissonovým rozdělením pravděpodobnosti s parametrem , resp. ); porovnejte (1) a (2) s (Zákon malých čísel 4 ). Přitom udává střední počet událostí v intervalu
a je tedy rovno určitému integrálu

(3)

Poznamenejme, že homogenní Poissonův proces dostaneme, když intenzita bude konstantní funkcí, . V takovém případě přímým výpočtem dostaneme střední počet událostí .

Nehomogenní Poissonův proces se často používá k modelování periodických náhodných jevů, např. příjezdů pacientů na ARO v závislosti na denní době. Jednoduchý tvar takové periodické intenzity může být např. tvaru

(4)

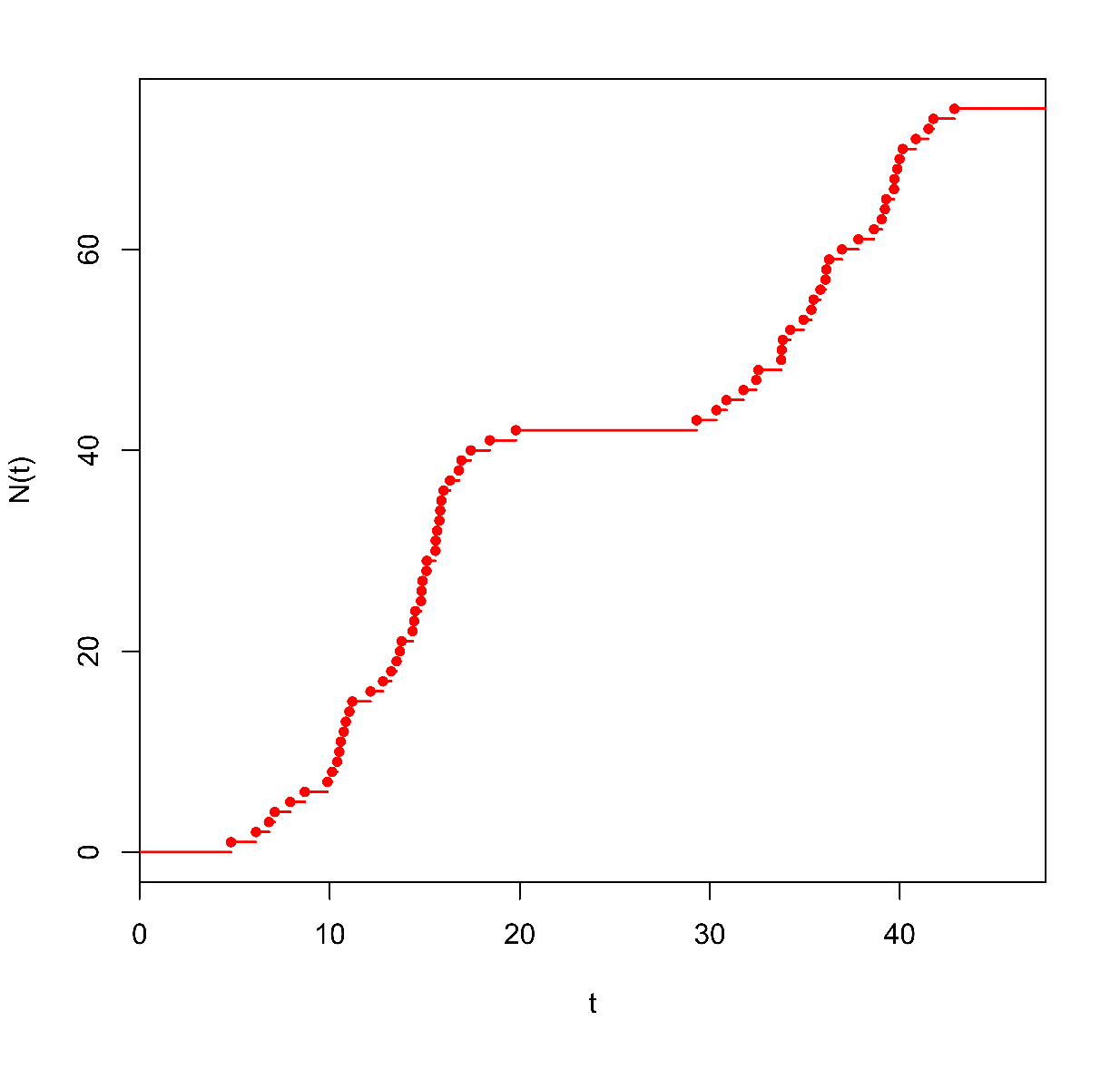
kde je konstantní část intenzity, udává amplitudu periodické části a je fázový posun. Veličina je úhlová frekvence, k periodě opakování je ve vztahu . Tedy např. pro nehomogenní Poissonův proces s intenzitou s denní periodou a časem uváděným v hodinách budeme mít úhlovou frekvenci . Příklad trajektorie nehomogenního Poissonova procesu s periodickou intezitou je na Obr.1.

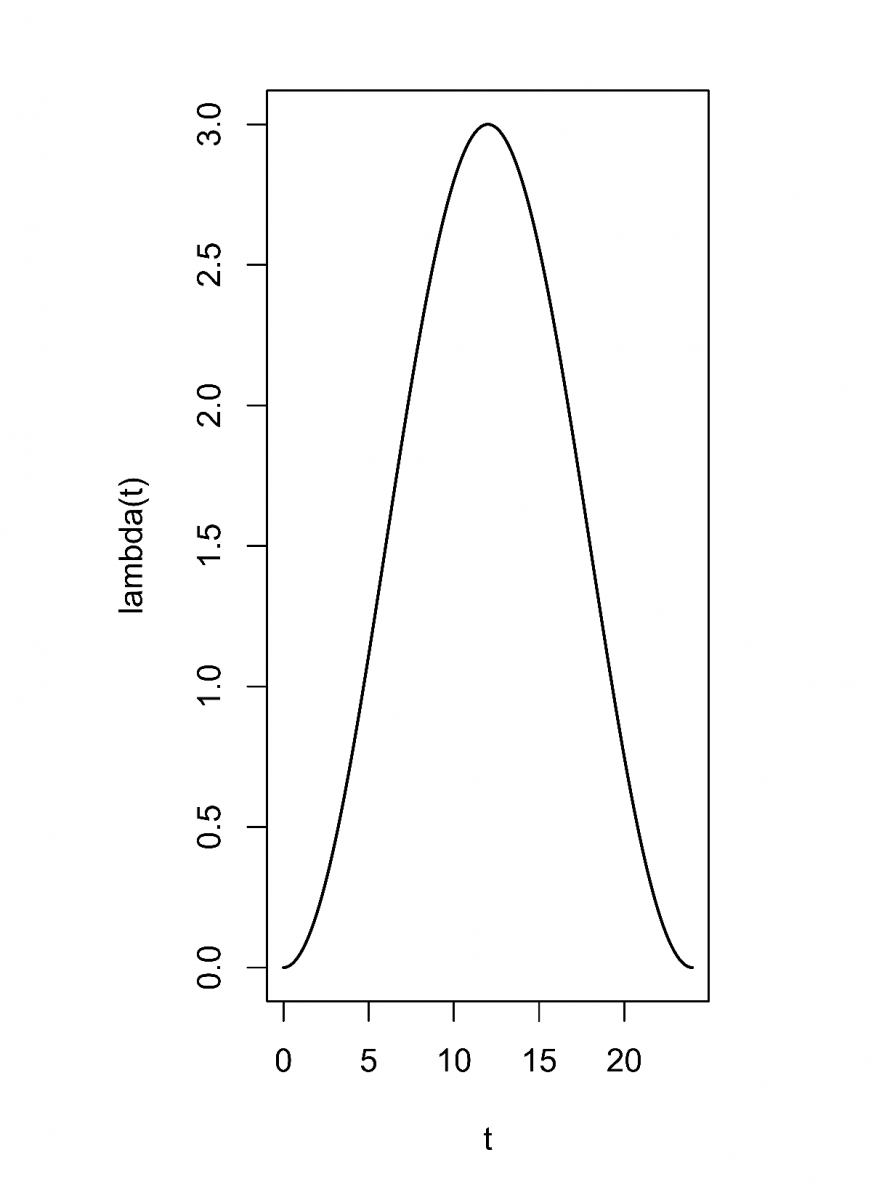
Obr.1: Vlevo: trajektorie nehomogenního Poissonova procesu s periodickou intenzitou eqref{eq:04-periodicka} s parametry ( a=b=1,5 ), h, . Je patrná velká hustota událostí v okolí časů 12 a 36 h, a velmi nízká hustota v okolí časů 0, 24 a 48 h, což odpovídá periodické intenzitě s periodou 24 h. Vpravo: průběh intenzity v závislosti na čase (v hodinách) po dobu jedné periody.

Proměnná intenzita však nemusí být jen deterministickou (nenáhodnou) funkcí času, , ale může záviset na hodnotě jiného náhodného procesu , stochasticky nezávislém na . Při takové volbě intenzity pak dostáváme tzv. Coxův proces.