Úvod do teorie informace

Zájemcům o hlubší pochopení principů teorie informace doporučujeme následující standardní literaturu, [1, 2, 3]. Uvedené zdroje zároveň sloužily jako zdroj textu této kapitoly. Příklady k procvičení jsou pak částečně inspirovány úkoly ze sbírky [4].

Základní problematika teorie informace byla vymezena americkým matematikem Claude Elwood Shannonem (1916-2001) v jeho práci A mathematical theory of communication z roku 1948, ve které dokázal klíčové teorémy o přenosu a reprezentaci informace. Shannonovou motivací byla  snaha exaktně popsat komunikaci, tedy způsob, jak ve zvoleném místě reprodukovat (přesně nebo přibližně) sdělení či signál vyslaný z  jiného místa.

Teorie informace ukazuje, že existují omezení na efektivitu reprezentace a spolehlivé komunikace sdělení:

1. Reprezentace informace:

   Sdělením, či signálem, mohou být hodnoty nějaké fyzikální veličiny (elektrického pole, frekvence zvuku, atp.) či symbolické abstrakce (písmena abecedy). Shannon ukázal, že sdělení lze popsat jako náhodný proces a přiřadit mu informační obsah v jednotkách bit (z anglického binary digit). V nejjednodušším případě je sdělení modelováno jako posloupnost nezávislých pozorování diskrétní náhodné veličiny s konečnou množinou stavů a pravděpodobnostní funkcí,

   (1)

   Průměrný informační obsah (v bitech) na jeden symbol takového sdělení je definován jako entropie veličiny

   (2)

   Význam entropie a zdůvodnění pojmu informační obsah spočívá v tom, že sdělení realizované veličinou nelze popsat méně než bity na symbol. Entropie tedy mimo jiné určuje dolní mez na bezeztrátovou kompresi dat, při nižší velikosti dat by již komprese musela být ztrátová.

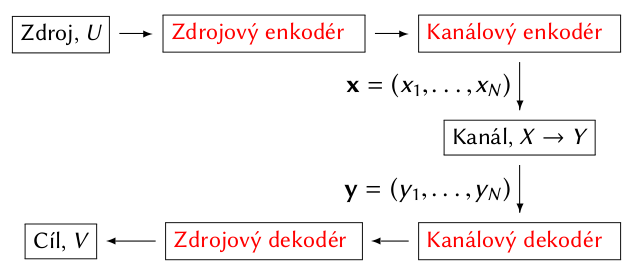
Obr. 1. Schéma přenosu informace dle C. E. Shannona.

Celý systém komunikující sdělení ze zdroje do cíle je znázorněn na obr. Vybraná témata z teorie informace 1. Sdělení realizované náhodnou veličinou je nejprve zdrojovým enkodérem komprimováno, v praxi často do podoby binárního řetězce. Tento binární řetězec je kanálovým enkodérem převeden na vstup do informačního kanálu. Sekvence vstupních symbolů (tzv. blokový kanálový kód) je kanálem zobrazena na výstupních symbolů, přičemž úkolem kanálového dekodéru je určit vstupní sekvenci s minimální pravděpodobností chyby. Výstup je v cíli dekomprimován zdrojovým dekodérem. Teoreticky lze v případě takovým systémem přenášet bitů na symbol a přitom zajistit, aby pravděpodobnost že zdrojové a cílové sdělení se liší byla libovolně malá. V praxi nebývá teoretických limitů dosaženo z důvodů přílišné výpočetní složitosti, zejména kanálového dekódování.