Trubice s nulovým tokem na okraji

V této a následující části prozkoumáme řešení rovnice difuze

(1)

za podmínky nulového toku na okraji trubice. Počáteční podmínku přitom stále předpokládáme ve tvaru

(2)

Nulový tok znamená, že první derivace koncentrace částic vzhledem k prostorové souřadnici je na okraji trubice nulová. V každém čase je tedy koncentrace částic v nějakém malém, ale celém,  okolí okraje konstantní, čímž zde nedochází k difuzi. To však neznamená, že koncentrace je také konstantní v čase. Nikoliv, během času se může měnit, ale tak, aby se v celém, malém, okolí okraje měnila stejným způsobem. Okrajová podmínka je tedy matematicky zapsána ve tvaru

(3)

Nulovost toku na okraji trubice, tzn. platnost Řešení rovnice difuze, 2. část (3) lze, podobně tomu bylo jako u nulové koncentrace na okraji, zajistit trikem. Symetricky vzhledem k okraji, tzn. bodu 0, umístíme zdánlivý zdroj(e) stejné koncentrace, jako je zadáno počáteční podmínkou. Počítáme tedy nyní s tzv. sudým rozšířením funkce

(4)

pomocí níž lze řešení difuzní rovnice Řešení rovnice difuze, 2. část (1) pro s počáteční podmínkou Řešení rovnice difuze, 2. část (2) a okrajovou podmínkou Řešení rovnice difuze, 2. část (3) zapsat jako

(5)

Abychom prozkoumali vliv sudého rozšíření, rozdělíme Řešení rovnice difuze, 2. část (5) na dva integrály a využijeme Řešení rovnice difuze, 2. část (4),

V prvním integrálu provedeme substituci a zaměníme meze. Tím budou oba integrály přes interval a lze řešení lze přepsat do tvaru

(6)

Vidíme, že v integrandu vystupuje součet hodnot dvou hustot normálního rozložení pravděpodobnosti: reálné a zdánlivé, umístěné symetricky vzhledem k okraji trubice, Tento princip zajistí nulový tok částic na okraji trubice, tedy platnost okrajové podmínky.

Stejně jako úlohách z předchozí kapitoly dále prozkoumáme speciální počáteční podmínku

(7)

Sudé rozšíření této počáteční podmínky je zřejmě

(8)

a řešení pak dle Řešení rovnice difuze, 2. část (5) či Řešení rovnice difuze, 2. část (6) s pomocí Řešení rovnice difuze (6) nalézáme ve tvaru -násobku součtu hodnot hustoty normálního rozdělení se střední hodnotou (poloha reálného zdroje) a rozptylem a hustoty normálního rozdělení se střední hodnotou (poloha zdánlivého zdroje) a stejným rozptylem,

(9)

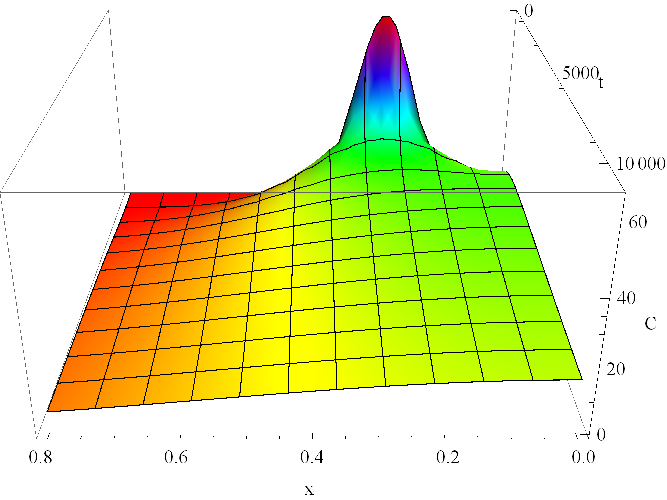
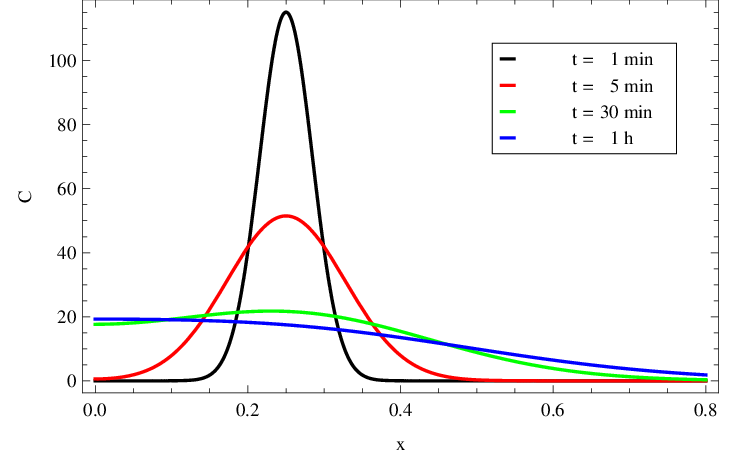
Řešení je zobrazeno v grafu na obr. Řešení rovnice difuze, 2. část 1. Rozložení koncentrace v trubici v několika časových okamžicích je pak zachyceno v obr. Řešení rovnice difuze, 2. část 2. Na průbězích z obr. Řešení rovnice difuze, 2. část 2 si zejména všimněme, že koncentrace na okraji, tzn. v bodě není nulová, dokonce se v čase mění. Jako funkce prostorové proměnné, však koncentrace na okraji dosahuje lokálního extrému, první parciální derivace koncentrace vzhledem k je zde skutečně nulová. Je zde tedy nulový tok, jak je předepsáno okrajovou podmínkou Řešení rovnice difuze, 2. část (3).

Obr. 1. Koncentrace C(x,t) v mM dle Řešení rovnice difuze, 2. část (9) v závislosti na prostorové souřadnici v cm a na čase v sekundách. Okrajovou podmínkou je stanoven nulový tok na okraji, x = 0, na počátku je v bodě a = 0,25 cm vloženo množství N0 = 10-6 mol částic. Průřez trubice má obsah S = 0,1 cm2, difuzní koeficient má hodnotu D = 10-5 cm2 s-1.

Obr. 2. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze, 2. část 1 v závislosti na (v cm) v několika časových okamžicích. Koncentrace na okraji není obecně nulová, ale vzhledem k prostorové proměnné zde má nulovou derivaci.