
Rychlost reakce
Absolutní hodnota derivace koncentrace substrátu je nazývána rychlostí reakce. Při quasi-steady-state aproximaci jsme odvodili vztahy Enzymová kinetika (35) a Enzymová kinetika (36). Pro okamžitou rychlost reakce v čase
tedy můžeme psát
|
|
(9) |
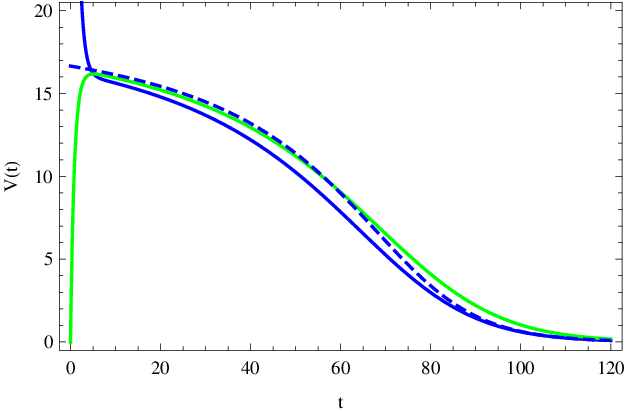
Graf závislosti této okamžité rychlosti na čase je vykreslen na obr. Enzymová kinetika, 2. část 2 čárkovanou čarou. Porovnáním s přesnými, numericky spočítanými, hodnotami derivací a
pro parametry Enzymová kinetika (20) vidíme, že Enzymová kinetika, 2. část (9) je relativně dobrou aproximací rychlosti reakce, s výjimkou krátké počáteční fáze. Na počátku je rychlost reakce aproximována hodnotou
 |
|
Obr. 2. Závislost okamžité rychlosti reakce V(t) podle Enzymová kinetika, 2. část (9) (modrá čárkovaná křivka, v mol dm-3 s-1) na čase t (v sekundách) podle Enzymová kinetika, 2. část (12) pro enzymovou reakci Enzymová kinetika (14) s parametry Enzymová kinetika (20). Přesné, numericky spočítané, hodnoty derivací koncentrací substrátu a produktu jsou zobrazeny plnými čarami, rychlost ubývání substrátu dS(t)/dt plnou modrou čarou a rychlost přibývání produktu dP(t)/dt plnou zelenou čarou.
|
Pro praktické využití je důležité chování (počáteční) rychlosti v závislosti na počáteční koncentraci substrátu
|
|
(10) |
Rychlost je rostoucí funkcí vzhledem k
a pro vysoké počáteční koncentrace substrátu
konverguje k maximu
|
|
(11) |
Lze tak psát
|
|
(12) |
 |
|
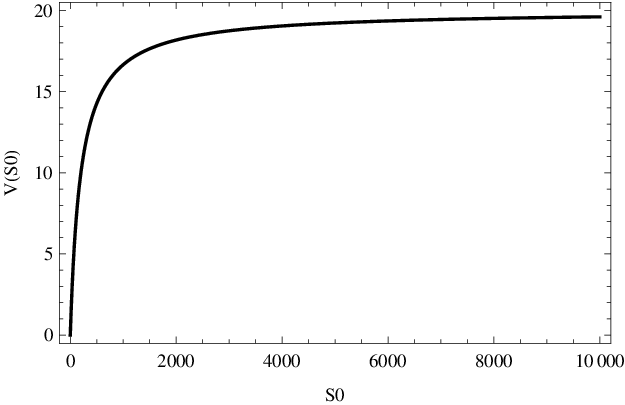
Obr. 3. Závislost (počáteční) rychlosti reakce V0 (mol dm-3 s-1) na počáteční koncentraci substrátu S0 (mol dm-3) podle Enzymová kinetika, 2. část (12) pro enzymovou reakci Enzymová kinetika (14) s parametry Enzymová kinetika (20).
|
 |
|
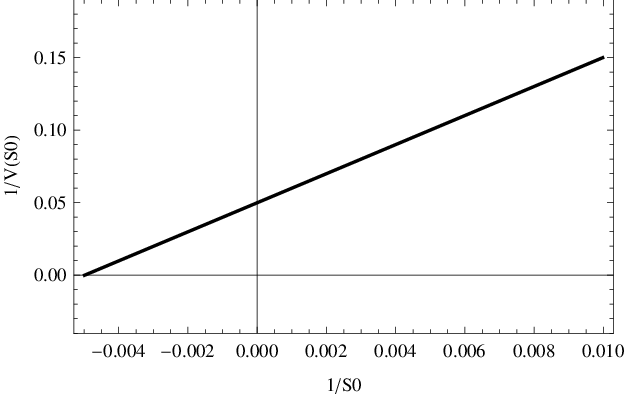
Obr. 4. Lineweaverův-Burkův graf závislosti Enzymová kinetika, 2. část (12). Na osách jsou vyneseny převrácené hodnoty veličin z obr. Enzymová kinetika, 2. část 3.
|
 |
|
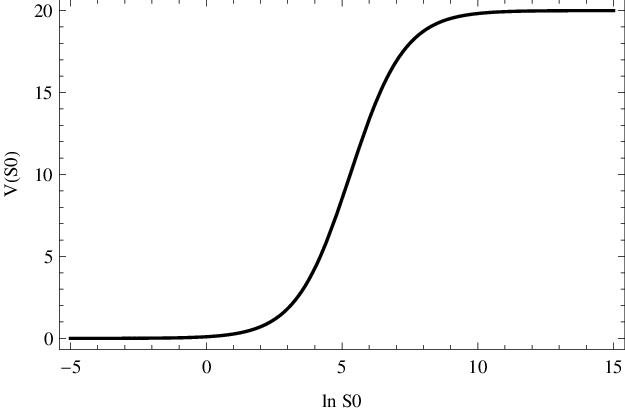
Obr. 5. Závislost Enzymová kinetika, 2. část (12) z obr. Enzymová kinetika, 2. část 3 ve tvaru sigmoidy. Na vodorovné ose je vynesen přirozený logaritmus počáteční koncentrace S0.
|
Graf rychlosti v závislosti na počáteční koncentraci substrátu je na obr. Enzymová kinetika, 2. část 3. Rychlost reakce roste s počáteční koncentrací substrátu, pro nízké počáteční hodnoty koncentrace je růst prudký, pro vysoké koncentrace se rychlost reakce přibližuje asymptotické maximální rychlosti
Z grafu lze odečíst, že pro počáteční koncentraci
je rychlost reakce rovna přibližně
V praxi často tato závislost zobrazuje na tzv. Lineweaverově-Burkově grafu, kdy se na svislou osu vynáší převrácená hodnota rychlosti, a na vodorovnou osu převrácená hodnota počáteční koncentrace substrátu,
jak je ukázáno v obr. Enzymová kinetika, 2. část 4. Takto zobrazená závislost je totiž lineární a toho v praxi se využívá k odhadu parametrů reakce. Empiricky se zjišťuje rychlost reakce
při různých počátečních koncentracích substrátu
Jejich převrácené hodnoty se vykreslí jako body v rovině, jimiž se proloží regresní přímka, např. pomocí klasické metody nejmenších čtverců.
Třetí možností, jak graficky zachytit stejnou závislost, je použitím logaritmického měřítka pro koncentraci. Na vodorovné ose je tedy vynesen přirozený (příp. desítkový) logaritmus koncentrace Odpovídající graf je na obr. Enzymová kinetika, 2. část 5, jedná se o tzv. sigmoidální křivku, neboli S-křivku. Ta roste z asymptotického minima 0 k asymptotickému maximu
a je symetrická vzhledem k inflexnímu bodu, pro nějž platí




