Trubice s podélným zdrojem a nulovou koncentrací na okraji

Předchozí počáteční podmínku nyní rozšíříme na podélný zdroj o koncentraci v intervalu mezi body a podél trubice. Máme tedy trubici s jedním okrajem, přičemž počáteční koncentrace částic v ní je popsána funkcí

(30)

Liché rozšíření počáteční podmínky je přitom zřejmě

(31)

Řešení difuzní rovnice Řešení rovnice difuze (1) pro s počáteční podmínkou Řešení rovnice difuze (30) a okrajovou podmínkou Řešení rovnice difuze (23) obdržíme dosazením do Řešení rovnice difuze (24),

V integrálech provedeme substituci a oba integrály poté s využitím Řešení rovnice difuze (8) přepíšeme jako rozdíly distribučních funkcí. Obdržíme výsledek

(32)

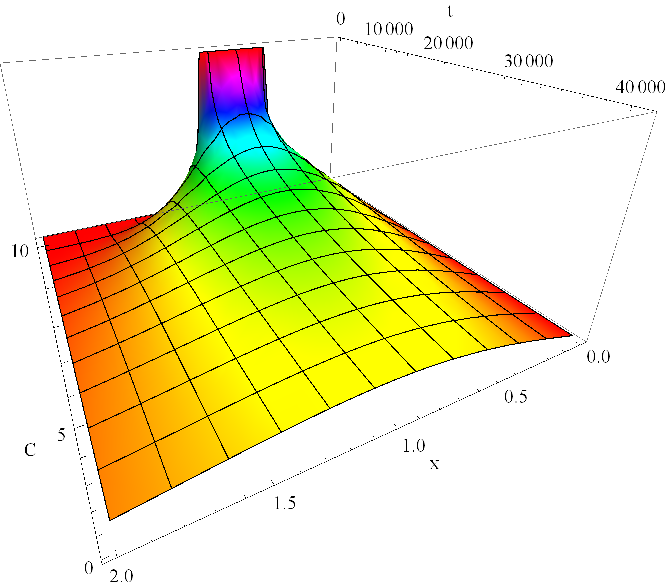
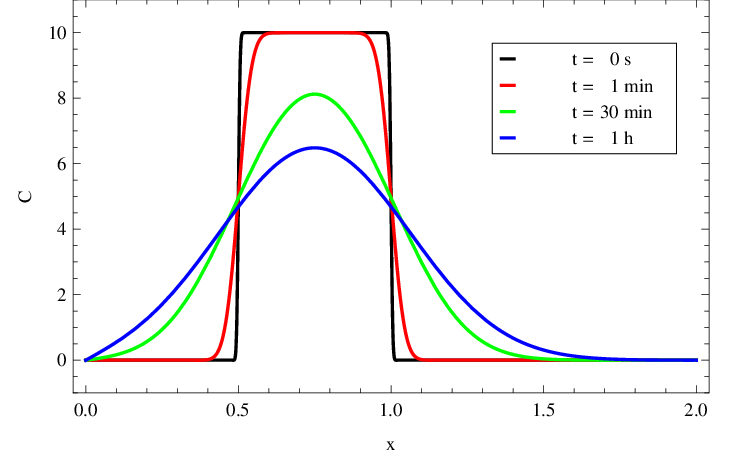
ve tvaru kombinace hodnot distribučních funkcí normálních rozdělení se středními hodnotami a stejným rozptylem Řešení je zobrazeno na grafu v obr. Řešení rovnice difuze 14. Rozložení koncentrace v trubici v několika časových okamžicích je zachyceno v obr. Řešení rovnice difuze 15. Je patrné vyhlazování prostorového rozložení s rostoucím časem, současně je reflektována okrajová podmínka nulové koncentrace.

Obr. 14. Koncentrace C(x,t) v mM dle Řešení rovnice difuze (32) v závislosti na prostorové souřadnici v cm a na čase v sekundách. Podélný počáteční zdroj částic o koncentraci C0 = 10-5 mol cm-3 je umístěn mezi body a = 0,5 cm a b = 1 cm. Difuzní koeficient je roven D = 10-5 cm2 s-1.

Obr. 15. Rozložení (x,t) v mM z obr. Řešení rovnice difuze 14 v závislosti na (v cm) v několika časových okamžicích.