Trubice s nulovou koncentrací na okraji

Přejdeme nyní k úlohám o trubici s jedním okrajem, který pro zjednodušení zápisu obvykle umisťován do bodu 0. Podobně jako u nekonečně dlouhé trubice lze i tento model s určitou nepřesností použít v případě trubice konečné délky, kdy druhý okraj je buď dostatečně vzdálený nebo koncentrace částic na něm není vnějším prostředím ovlivňována.

Uvažujeme tedy trubici s jedním okrajem, přičemž počáteční koncentrace částic v ní je popsána funkcí

(22)

Na okraji trubice je koncentrace částic stále udržována na nulové hodnotě, tedy tzv. okrajová podmínka je tvaru

(23)

Řešení difuzní rovnice Řešení rovnice difuze (1) pro s počáteční podmínkou Řešení rovnice difuze (22) a okrajovou podmínkou Řešení rovnice difuze (23) je obvykle uváděno jako

(24)

kde je tzv. liché rozšíření funkce

(25)

Můžeme si virtuálně představit nekonečnou trubici, v níž je v bodě zdroj počáteční koncentrace a v bodě tedy symetricky vzhledem k okraji skutečné trubice, je místo, z něhož jsou částice stejnou rychlostí odčerpávány. Tato konfigurace zajistí nulovou koncentraci částic v bodě tedy splnění okrajové podmínky, díváme-li se jen na polovinu trubice. Tvar řešení je principiálně stejný jako řešení Řešení rovnice difuze (11), ale vystupuje v něm liché rozšíření počáteční podmínky.

Aby byl vliv lichého rozšíření na řešení více patrný, rozdělíme Řešení rovnice difuze (24) na dva integrály a využijeme Řešení rovnice difuze (25),

V prvním integrálu následně provedeme substituci a zaměníme meze. Tím budou oba integrály přes interval a lze řešení lze přepsat do tvaru

(26)

Vidíme, že v integrandu vystupuje rozdíl hodnot dvou hustot normálního rozložení pravděpodobnosti: reálné a zdánlivé, umístěné symetricky vzhledem k okraji trubice, Právě tento princip zajistí nulovou koncentraci částic na okraji trubice, tedy platnost okrajové podmínky.

Uvažujme dále speciální případ

(27)

kdy je v čase vypuštěno množství částic v místě trubice o ploše průřezu Liché rozšíření této počáteční podmínky je zřejmě (např. si načrtněte graf)

(28)

a řešení pak dle Řešení rovnice difuze (24) či Řešení rovnice difuze (26) s pomocí Řešení rovnice difuze (6) nalézáme ve tvaru násobku rozdílu hodnot hustoty normálního rozdělení se střední hodnotou (poloha reálného zdroje) a rozptylem a hustoty normálního rozdělení se střední hodnotou (poloha zdánlivého zdroje) a stejným rozptylem,

(29)

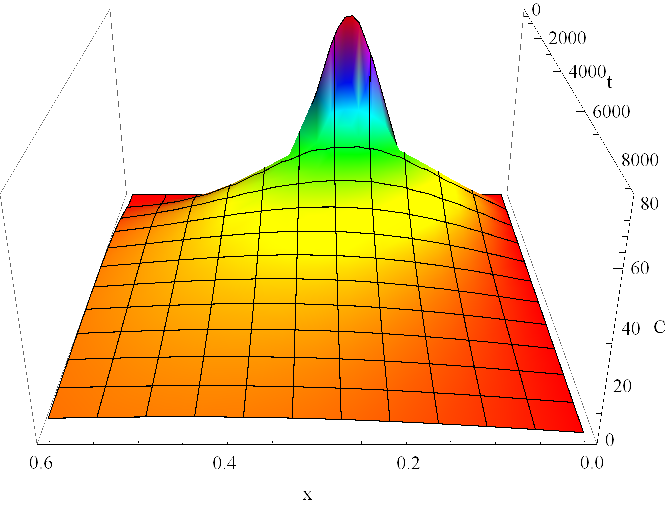
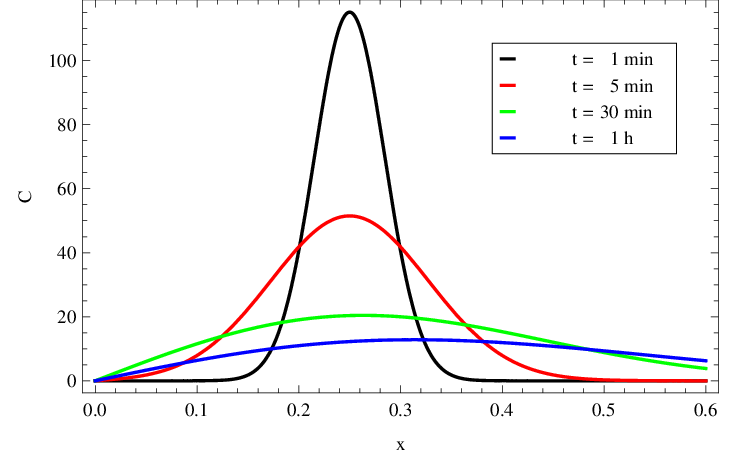
Řešení je zobrazeno na grafu v obr. Řešení rovnice difuze 12. Rozložení koncentrace v trubici v několika časových okamžicích je zachyceno v obr. Řešení rovnice difuze 13. Průběh řešení je podobný řešení pro nekonečnou trubici, zde však máme řešení jen na poloprostoru a navíc je reflektována okrajová podmínka nulové koncentrace.

Obr. 12. Koncentrace C(x,t) v mM dle Řešení rovnice difuze (29) v závislosti na prostorové souřadnici v cm a na čase v sekundách. Hodnoty parametrů jsou a = 0,25 cm,  N0 = 10-6 mol, S = 0,1 cm2, D = 10-5 cm2 s-1.

Obr. 13. Rozložení C(x,t) v mM z obr. Řešení rovnice difuze 12 v závislosti na (v cm) v několika časových okamžicích.