Makroskopický pohled a Fickův zákon

V předchozí části jsme zkoumali mikroskopický pohyb jedné konkrétní částice. Proces difuze jsme modelovali zobecněnou náhodnou procházkou, rovnici difuze a její obecné řešení jsme nalezli zkoumáním pravděpodobnostních vlastností tohoto modelu. V této části rovnici difuze odvodíme pomocí makroskopické teorie difuze. Prostředkem matematického modelování difuze bude popis koncentrace zkoumaných částic (objektů) a jejich změn v čase a prostoru. Při odvození se opět omezíme na jednorozměrný prostor, reprezentovaný dutým válcem o konstantním průřezu umístěným podél -ové osy.

Než odvodíme tzv. Fickův zákon a rovnici difuze, popíšeme si použité fyzikální veličiny. Koncentrací rozumíme počet částic na jednotkový objem v místě a čase Počet částic v určité oblasti je pak rovný součinu koncentrace a objemu oblasti, za předpokladu, že koncentrace je ve všech místech stejná, což bude splněno např. když oblast bude dostatečně malá. Počet částic v části dutého válce o průřezu umístěného podél -ové osy a o dostatečně malé délce je tedy přibližně roven

Rychlostí ryzího vzniku rozumíme veličinu udávající rozdíl počtu nově vzniklých (dodaných) a zaniklých (odebraných) částic na jednotkový objem a jednotkový čas v místě a čase Je-li částice v dané oblasti vznikají, je-li částice v dané oblasti zanikají. Rozdíl počtu vzniklých a zaniklých částic v části dutého válce o průřezu a dostatečně malé délce za časový interval je přibližně roven součinu rychlosti ryzího vzniku, objemu oblasti a délky časového intervalu,

Veličina čistý tok popisuje množství částic, které za jednotku času překročí plochu o jednotkovém obsahu kolmou na osu v daném místě a čase přičemž částice procházející touto plochou ve směru kladné -ové poloosy se započítávají s kladným znaménkem a částice procházející ve směru opačném se započítávají se znaménkem záporným. Je-li větší množství částic se pohybuje přes plochu v kladném směru, pokud větší množství částic se pohybuje přes plochu ve směru záporném. Rozdíl počtu částic, které projdou plochou o obsahu kolmou na osu v bodě za časový interval délky v kladném a záporném směru, je pak rovný součinu

Z uvedených vyjádření lze již nyní určit jednotky uvedených veličin. Zůstaneme u obvyklého vyjádření počtu částic pomocí molárního množství, tedy jednotkou mol. Budeme-li délku vyjadřovat v centimetrech a obsah v koncentrace vyjadřující počet částic v jednotkovém objemu bude mít jednotku Aby platily výše uvedené vztahy, musí pak mít rychlost ryzího vzniku jednotku a čistý tok musí být vyjádřen v jednotkách

Vezměme si dvě nepříliš vzdálená místa trubice, a  Předpokládejme, že známe koncentrace částic v těchto místech v čase a klademe si otázku, kolik částic se přemístí přes jednotkovou plochu mezi těmito dvěma body za časový okamžik Jaký je čistý tok trubicí v prostoru mezi uvažovanými dvěma body? Sledujme schéma na obr. Difuze 2.

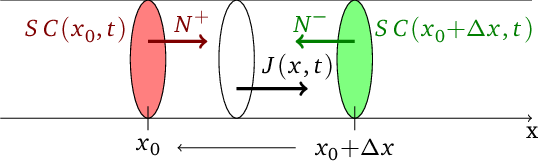Obr. 2. Schéma k odvození 1. Fickovy rovnice, Difuze (28). Uvažujeme válec o průřezu S a délce umístěný podél x-ové osy, s čely v bodech x0 a x0 + . V místě levého čela je S, C(x0,t) částic na jednotkovou délku válce, analogicky v místě pravého čela je S, C(x0,t) částic na jednotkovou délku válce. Za dobu přejde N+ částic z levého čela doprava a N- částic z pravého čela směrem doleva. Tok J(x,t) částic bodem x uvnitř válce obdržíme uvážením chování při limitního zkrácení válce na nulovou délku.

Pohyb částic modelujeme symetrickou zobecněnou náhodnou procházkou. Během časového intervalu se polovina částic z bodu přesune do bodu tedy v kladném směru osy těch je

Naopak polovina částic původně v místě se dostane do bodu tedy v záporném směru osy jejich počet je

Čistý tok válcem mezi body a je dán rozdílem  vyděleným plochou průřezu válce a délkou časového intervalu,

(26)

Zlomky na pravé straně zkrátíme obsahem průřezu a rozšíříme členem . Po přeuspořádání dostaneme

(27)

Provedeme limitní přechod  tak, aby podíl zůstal konečný. Tím přejde bod uvnitř uvažovaného intervalu do bodu V prvním zlomku na pravé straně Difuze (27) rozpoznáme difuzní koeficient Difuze (13), druhý zlomek přejde v parciální derivaci koncentrace podle v bodě Po formálním přeznačení na obecný bod (na volbě polohy uvažované části válce nezáleží) obdržíme tzv. 1. Fickovu rovnici

(28)

Ta vyjadřuje tzv. Fickův zákon, který říká, že čistý tok v bodě a čase je úměrný prostorové derivaci koncentrace v tomto bodě, přičemž konstanta úměrnosti je zápornou hodnotou difuzního koeficientu, Všimněme si záporného znaménka, které vyjadřuje že kladný tok směřuje do místa s nižší koncentrací. Zároveň je zřejmé zahrnutí faktoru  do definice difuzního koeficientu dle Difuze (13), aby zápis Difuze (28) by co nejjednodušší. Z Difuze (28) také lehce ověříme, že jednotkou musí být Poznamenejme, že obecně může být difuzní koeficient funkcí koncentrace , resp. polohy a času V takovém případě se často používá k aproximaci závislosti na Taylorova rozvoje vhodného řádu.

Pokud je parciální derivace koncentrace částic v bodě podle nulová, je v bodě tok nulový, Prostorové rozložení částic v okolí bodu se nemění, systém je v rovnováze. Zdůrazněme, že rozložení částic se však stále může měnit v čase, parciální derivace vhledem k není nijak omezena. Pokud je v pevném čase tok v bodě konstantní, má v tomto čase prostorové rozložení koncentrace částic v okolí bodu tvar lineární funkce

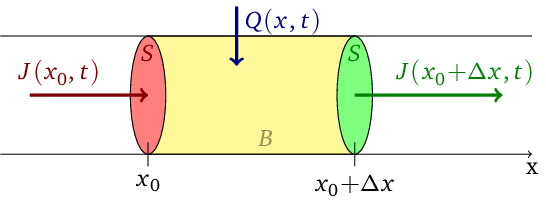
Pro další odvození budeme opět uvažovat část  válce mezi body a umístěného podél -ové osy, jak je ukázáno na obr. Difuze 3. Obě čela (podstavy) válce mají obsah Objem zkoumané části válce je tak rovný Obecný zákon rovnováhy říká, že změna počtu částic v o objemu za dobu je rovna součtu počtu nově vzniklých částic uvnitř a čistého počtu částic, které přešly přes obě čela (hranice) dovnitř

Obr. 3. Schéma k odvození 2. Fickovy rovnice, Difuze (33). Uvažujeme válec B o průřezu S a délce umístěný podél x-ové osy, s čely v bodech x0 a x0 + . Toky částic čely válce B jsou rovny J(x0,t), resp. J(x0 + ,t), čistá rychlost vzniku částic (vnější příčinou) v bodě x uvnitř B je rovna Q(x,t).

Počet částic v je (obecně při nekonstantní koncentraci) rovný

Změna počtu částic za časový interval je rovna rozdílu

Čistý počet nově vzniklých částic uvnitř za dobu je dán výrazem

Čistý počet částic, které přešly přes čelo dovnitř je rovný Analogicky, přes čelo přejde částic dovnitř Záporné znaménko je zde proto, že tok částic čelem dovnitř je v negativním směru osy Matematický zápis zákonu rovnováhy je tedy tvaru

	(29)

Rovnici vydělíme výrazem čímž přejde do tvaru

	(30)

Za předpokladu spojitosti použitých funkcí použijeme ve všech třech integrálech Lagrangeovu větu o střední hodnotě. Podle ní existují tři (ne nutně různé) body takové, že Difuze (30) lze napsat ve formě

(31)

Celou rovnici vydělíme

(32)

a provedeme limitní přechod Tím body přejdou v na levé straně dostaneme parciální derivaci koncentrace podle času a na pravé straně parciální derivaci toku podle Po přeznačení na obecné  dostáváme tzv. 2. Fickovu rovnici

(33)

Dosazením Difuze (28) do pravé strany Difuze (33) a za podmínky obdržíme

(34)

což je tzv. rovnice difuze. Porovnáním s Difuze (25) zjistíme, že se matematicky jedná o tu samou diferenciální rovnici. Tvar Difuze (25) jsme však odvodili pro pravděpodobnost výskytu jedné částice, zatímco Difuze (34) popisuje koncentraci všech částic v daném místě a čase. Obecný tvar řešení této parciální diferenciální rovnice je uveden v úkolu Cvičení 1, více se mu pak budeme věnovat v následující kapitole.

S touto rovnicí se lze setkat nejen u difuze. Pokud veličina popisuje teplotu tyče v daném místě a čase, nazývá se Difuze (34) rovnicí vedení tepla. Kromě modelování biochemických a biofyzikálních procesů se rovnice difuze využívá např. také ve finanční matematice pro popis závislosti ceny akcie a opce. Z pohledu matematické analýzy se jedná o parciální diferenciální rovnici 2. řádu parabolického typu. Jako u jedné z mála parciálních diferenciálních rovnic známe exaktní postupy pro nalezení řešení za různých počátečních, koncových a okrajových podmínek. Tvary řešení některých z těchto situací si ukážeme v další kapitole tohoto výukového materiálu.

Ve vyšších dimenzích prostoru se difuzní rovnice odvozuje analogicky, přičemž výše uvedené principy se aplikují složky pohybu částic ve směrech jednotlivých os. Ve dvourozměrném prostoru tak má rovnice difuze pro koncentraci v bodě a čase tvar

(35)

Podobně, ve třírozměrném prostoru se rovnice difuze pro popis koncentrace částic obvykle zapisuje ve tvaru

(36)

kde vystupuje tzv. Laplaceův operátor (nabla na druhou),

(37)

Na závěr uvedeme ještě speciální, ale v praxi častý, případ difuze v třírozměrném prostoru. Jedná se o sféricky symetrický model, kdy jsou podmínky difuze stanoveny tak, aby koncentrace částic v prostoru byla vždy v konkrétním čase konstantní na celé sféře kolem počátku. Pro popis modelu pak místo tří prostorových souřadnic stačí jen jedna proměnná, a to vzdálenost od počátku

Rovnice Difuze (36) se klasickou transformací z kartézských do sférických souřadnic převede na tvar

(38)

Obecný tvar řešení této parciální diferenciální rovnice je uveden v úkolu Cvičení 2, vrátíme se k němu i v následující kapitole.