Quasi-steady-state aproximace

Z původních čtyř rovnic zůstala soustava dvou diferenciálních rovnic Enzymová kinetika (24), Enzymová kinetika (25) s podmínkami Enzymová kinetika (19). Ani tento systém však není řešitelný ve smyslu nalezení analytického tvaru formulí pro obě koncentrace. V takové situaci, jenž je v matematickém modelování celkem běžná, se snažíme pokročit s řešením tím, že některé závislosti v modelu potlačíme a úlohu tak zjednodušíme. Po nalezení řešení se vrátíme do místa, kde jsme model zjednodušili a prodiskutujeme, jak výrazný dopad má zvolené omezení na reálnou situaci a jak by bylo řešení ovlivněné, kdybychom pracovali s původním nezjednodušeným modelem.

V obr. Enzymová kinetika 2 si všimněme toho, že za dobu 5 s od začátku reakce klesne koncentrace substrátu (modrá křivka) asi o 15 %, zatímco koncentrace enzymu (černá křivka) se za stejnou dobu sníží přibližně o 80 %. Vzhledem k rychlosti změn koncentrace enzymu a tím i koncentrace komplexu, je tedy koncentrace substrátu skoro neměnná. Představme si tedy, že reakce je na začátku svého průběhu a předpokládejme poněkud radikální zjednodušení, že koncentrace substrátu se v čase nemění, např. proto, že jeho množství je velké, nebo je substrát neustále doplňován. Rovnice Enzymová kinetika (25) je nyní irelevantní a Enzymová kinetika (24) pro jedinou neznámou koncentraci komplexu přejde do tvaru

(26)

s počáteční podmínkou

Řešením této diferenciální rovnice je funkce

(27)

kde

(28)

je asymptotická hodnota koncentrace komplexu, které je pro dosaženo nezávisle na počáteční hodnotě

(29)

je tzv. Michaelisova konstanta a

(30)

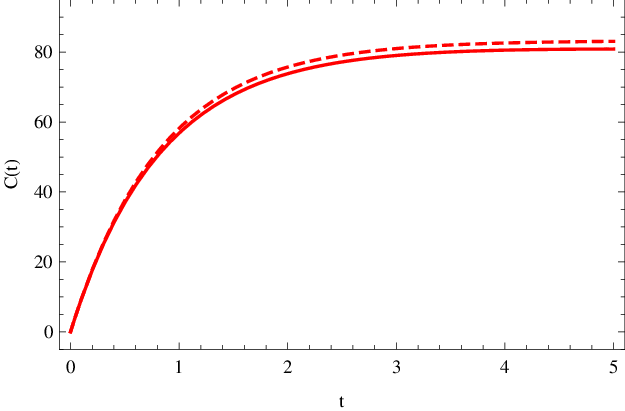
Zdůrazněme fakt, že asymptotická koncentrace komplexu závisí na rychlostních konstantách pouze prostřednictvím Michaelisovy konstanty tedy prostřednictvím vhodného poměru rychlostních konstant. Pro uvažované hodnoty parametrů Enzymová kinetika (20) dostáváme hodnotu Michaelisovy konstanty a asymptotickou koncentraci Vývoj hodnoty koncentrace za podmínky konstantní koncentrace substrátu během prvních 5 s reakce je vykreslena v obr. Enzymová kinetika 4 (čárkovaná křivka). Pro porovnání je přikresleno i přesné řešení (plnou čarou) z obr. Enzymová kinetika 1. Vidíme, že koncentraci komplexu lze velmi dobře aproximovat hodnotou Enzymová kinetika (27). Přitom si můžeme dovolit považovat koncentraci substrátu za konstantní, rovnu na intervalu až do doby 5 s po začátku reakce.

Obr. 4.Koncentrace komplexu C(t) (mol dm-3) v závislosti na čase t (sekundy) pro počáteční fázi reakce. Čárkovaná křivka znázorňuje přibližnou hodnotu dle Enzymová kinetika (27) za  podmínky konstantní koncentrace substrátu, plnou čarou je vyznačený přesný, numericky spočítaný, průběh koncentrace.

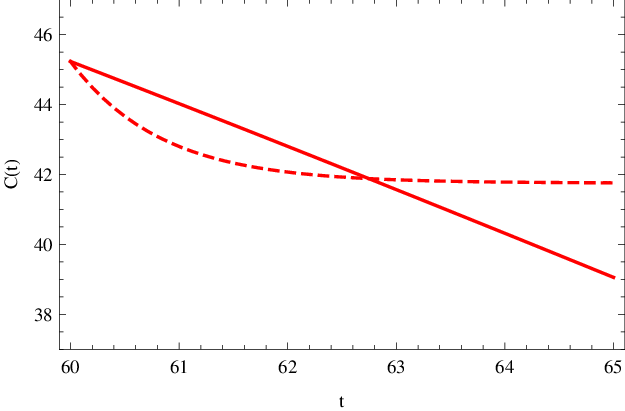
Analogicky lze tuto aproximaci aplikovat i v průběhu reakce, jak je ukázáno v obr. Enzymová kinetika 5, kde je předpoklad konstantní koncentrace substrátu použit po 60 s od počátku reakce. Je však patrné, že aproximace je v tomto případě méně přesná, a lze ji rozumně použít asi po dobu 3 s, pro delší časové intervaly se již hodnota koncentrace značně odlišuje od přesného řešení.

Obr. 5. Koncentrace komplexu C(t) (mol dm-3) v závislosti na čase t (sekundy) po 60 s od počátku reakce. Čárkovaná křivka znázorňuje přibližnou hodnotu dle Enzymová kinetika (27) za podmínky konstantní koncentrace substrátu, plnou čarou je vyznačený přesný, numericky spočítaný, průběh koncentrace.

S rostoucím časem se koncentrace komplexu mění pomaleji (derivace klesá k nule) a Enzymová kinetika (27) se blíží limitě dle Enzymová kinetika (28). Není tedy překvapením, že je řešením rovnice

(31)

pro rovnovážný stav, kterou obdržíme tak, že v Enzymová kinetika (26) uvažujeme

Vraťme se nyní zpět ke vztahu Enzymová kinetika (25) pro koncentraci substrátu a uvažujme, co se na výše uvedeném přístupu změní, když nebude konstantní, ale bude se v čase měnit. Tvrdíme, že v tom případě bude dobrou aproximací koncentrace komplexu v libovolném čase asymptotická hodnota podle Enzymová kinetika (28), v níž namísto dosadíme okamžitou hodnotu koncentrace Představíme-li si Enzymová kinetika (28) jako funkci koncentrace substrátu můžeme tedy psát

(32)

Pokud se koncentrace substrátu bude měnit pomalu vzhledem k rychlosti změn koncentrace komplexu bude koncentrace dobře aproximována tzv. quasi-steady-state rovnicí

(33)

Tento důležitý výsledek se nazývá quasi-steady-state (pseudo-steady-state) řešením, neboť jej obdržíme také tím, že levou stranu Enzymová kinetika (24) položíme rovnou 0 a rovnici vyřešíme pro Předpokládáme tedy, že koncentrace komplexu je ustálená, přestože ve skutečnosti konstantní není. Stačí jen zajistit, aby se koncentrace měnila tak pomalu, že koncentrace se chová, jako by bylo po určitou (krátkou) dobu konstantní.

Jaká koncentrace substrátu odpovídá quasi-steady-state aproximaci koncentrace komplexu? Dosazením Enzymová kinetika (33) do Enzymová kinetika (25) obdržíme diferenciální rovnici

(34)

Vytkneme výraz z pravé strany Enzymová kinetika (33) a po úpravě dostaneme

(35)

Porovnáním zjistíme, že tzn. quasi-steady-state aproximace udává, po vynásobení rychlostní konstantou rychlost změny koncentrace substrátu. Diferenciální rovnici pro odpovídající časový vývoj koncentrace produktu obdržíme dosazením Enzymová kinetika (33) do pravé strany Enzymová kinetika (18),

(36)

Řešení rovnice Enzymová kinetika (35) lze nalézt v implicitním tvaru

(37)

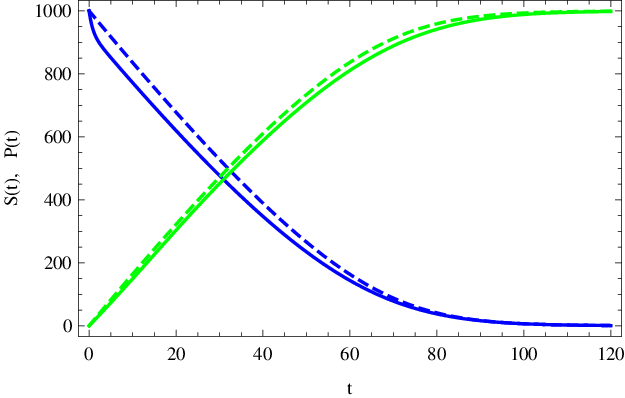
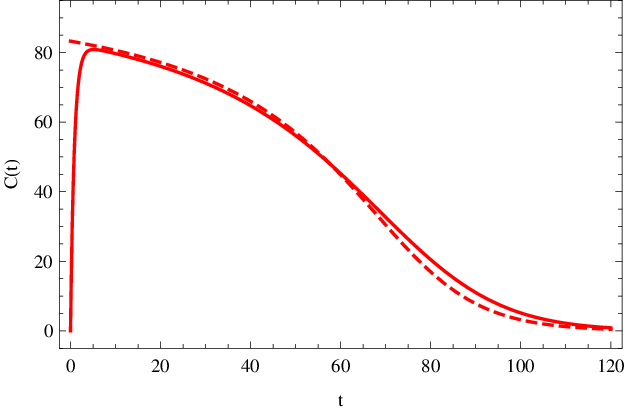
To nám umožňuje graficky znázornit (např. pomocí parametricky zadaných křivek) průběhy koncentrací substrátu a produktu na čase při quasi-steady-state aproximaci. Výsledné průběhy jsou vykresleny (čárkované křivky) v obr. Enzymová kinetika 6. Na obr. Enzymová kinetika 7 je potom vykresleno (čárkovanou křivkou) quasi-steady-state řešení koncentrace komplexu Enzymová kinetika (33). Vidíme, že při splnění výše uvedených podmínek je aproximace pro globální popis průběhu reakce dostačující.

Obr. 6. Koncentrace substrátu S(t) (modře) a produktu P(t) (zeleně) (mol dm-3) v závislosti na čase t (sekundy). Čárkované křivky znázorňují quasi-steady-state řešení dle Enzymová kinetika (35) a Enzymová kinetika (36), plnou čarou jsou nakresleny přesné, numericky spočítané, průběhy koncentrací podle kinetického schématu Enzymová kinetika (14) s parametry Enzymová kinetika (20).

Obr. 7. Koncentrace komplexu C(t) (mol dm-3) v závislosti na čase t (sekundy). Čárkovaná křivka znázorňuje quasi-steady-state řešení dle Enzymová kinetika (33), plnou čarou je nakresleno přesný, numericky spočítaný, průběh koncentrace podle kinetického schématu Enzymová kinetika (14) s parametry Enzymová kinetika (20).

Porovnáním derivací Enzymová kinetika (35) a Enzymová kinetika (36) zjistíme, že důsledkem quasi-steady-state aproximace je konstantní součet koncentrací substrátu a produktu, což se na obrázku projeví vertikální symetrií čárkovaných křivek. Připomeňme, že pro přesná řešení systému diferenciálních rovnic však toto neplatí, viz obr. Enzymová kinetika 3.