Radiální difuze z mikropipety

Na závěr si ukážeme řešení triviálního případu difuze v třírozměrném prostoru. Mikropipeta je naplněna částicemi fluorescenční látky a její konec je vložen přibližně do středy nádoby s vodou. V čase do vodního prostředí vstříknuto množství fluorescenční látky a ta se difuzí šíří rovnoměrně všemi směry. Sledujeme vývoj koncentrace v čase v okolí tohoto místa.

Vzhledem k tomu, že vlastnosti vodního prostředí jsou ve všech směrech stejné, jedná se o sféricky symetrickou úlohu Difuze (38). Řešíme tedy rovnici

(21)

pro čas a proměnnou popisující vzdálenost od místa vstříknutí fluorescenční látky. Počáteční podmínka je matematicky zapsána ve tvaru

(22)

kde je třírozměrná delta-funkce. Ta je odlišná od jednorozměrné delta-funkce, neboť je definována jako limitní případ třírozměrného rovnoměrného, resp. třírozměrného normálního rozdělení pravděpodobnosti. Pro popis třírozměrné delta-funkce nám však bude stačit následující vyjádření pomocí jednorozměrné delta-funkce,

(23)

z něhož je patrné, že rozměr funkce je rovný převrácené hodnotě třetí mocniny jednotky veličiny

Difuzní rovnice Řešení rovnice difuze, 2. část (21) s počáteční podmínkou Řešení rovnice difuze, 2. část (22) má řešení tvaru

(24)

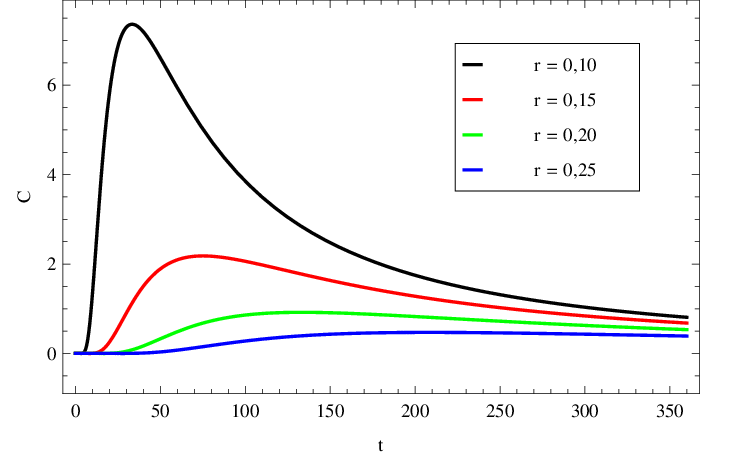
Jedná se vlastně o hustotu pravděpodobnosti centrovaného třírozměrného normálního rozdělení pravděpodobnosti s diagonální kovarianční maticí a homogenním rozptylem, kde místo proměnných vystupuje pouze veličina Časový vývoj koncentrace na sférách v několika vzdálenostech od počátku je zobrazen v grafu na obr. Řešení rovnice difuze, 2. část 10. Pozorujeme obecně podobný tvar jako v obr. Řešení rovnice difuze, 2. část 9, ve třírozměrném prostoru je však pokles koncentrace po dosažení maxima rychlejší.

Obr. 10. Průběh koncentrace C(r,t) (v M) v třírozměrném prostoru podle Řešení rovnice difuze, 2. část (24) v závislosti na čase (v sekundách) na sférách o vzdálenosti r (v centimetrech) od místa, kde bylo na počátku experimentu vstříknuto N0 = 0,1 mol fluorescenční látky o difuzním koeficientu D = 5.10-5cm2s-1.

Jak se průběh koncentrace změní, když látka nebude vstříknuta najednou, ale celé množství bude z mikropipety uvolňováno rovnoměrně, rychlostí během intervalu délky ? Řešíme tak difuzní rovnici Řešení rovnice difuze, 2. část (21) s podmínkou na rychlost přidávání částic v bodě a čase

(25)

Závislost koncentrace na čase a vzdálenosti od počátku získáme integrováním Řešení rovnice difuze, 2. část (24) přes časovou proměnnou v intervalu Obdržíme výsledek

(26)

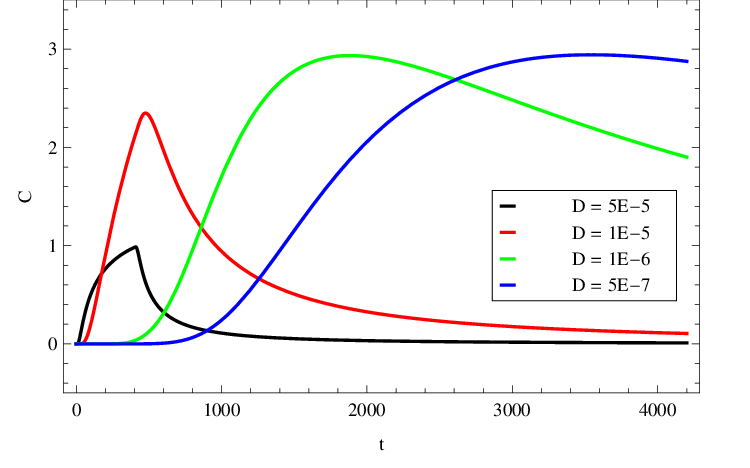
v němž vystupují hodnoty distribuční funkce podle Řešení rovnice difuze (8). Závislosti na čase jsou vykresleny v obr. Řešení rovnice difuze, 2. část 11 pro několik různých hodnot difuzního koeficientu  Pro velké hodnoty koncentrace velmi rychle reaguje na ukončení vstřikování látky v čase Pro malé hodnoty je difuze pomalá, a dosažení čas dosažení maximální koncentrace je několikanásobně delší, než doba

Obr. 11. Průběh koncentrace C(r,t) (v M) v třírozměrném prostoru podle Řešení rovnice difuze, 2. část (24) v závislosti na čase (v sekundách) na sféře o vzdálenosti  r = 1 mm od místa, kde bylo po dobu t0 = 400 sekund od počátku experimentu rovnoměrnou rychlostí vstřikováno celkové množství N0 = 0,1 mmol fluorescenční látky. Závislosti jsou uvedeny pro různé hodnoty difuzního koeficientu D (v cm2 s-1).