Časová škála

V předešlé kapitole jsme jako argument pro aproximaci používali předpoklad, že jedna funkce se mění pomaleji než funkce jiná. Tento vágně formulovaný pojem si nyní definujeme přesně. Matematicky je rychlost změny funkce kvantifikována derivací dané funkce. Porovnávání derivací funkcí je však v praxi problematické z důvodu, že hodnoty funkcí a tím i jejích derivací mohou být vyjádřeny v různých jednotkách. Proto neporovnáváme přímo derivace funkcí, ale délky časových intervalů, během nichž dochází k největším změnám v hodnotách funkcí.

Dostáváme se tak k pojmu časové škály, time scale. Poznamenejme, že tento pojem je užíván zejména v matematické analýze, kde umožňuje spojit a zobecnit teorii diferenčních a diferenciálních rovnic. Pro náš účel zavedeme pojem time scale, funkce jako nejkratší dobu potřebnou k tomu, aby se funkční hodnota co nejvíce změnila, a to maximální rychlostí. Jde tedy o podíl maximálního možného rozdílu funkčních hodnot ku maximální absolutní hodnotě derivace, tzn.

(1)

přičemž uvedená infima a suprema se počítají přes interval časů který je předmětem modelování.

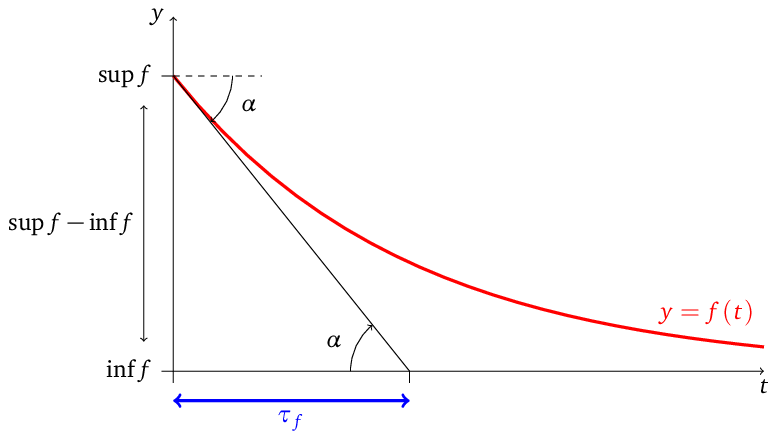
Obr. 1. Grafické určení time scale (délka modré úsečky) funkce f(t) (červená křivka) tvaru klesající exponenciály.

Z matematické analýzy je známo, že derivace funkce v bodě má geometrický význam směrnice tečny ke grafu funkce v tomto bodě. Výraz tedy udává směrnici tečny ke grafu funkce v bodě, kde je sklon (tzn. absolutní hodnota derivace) funkce největší. Směrnice tečny je dále rovna tangens úhlu který tečna svírá s kladnou vodorovnou poloosou. Rovnici Enzymová kinetika, 2. část (1) tedy můžeme přepsat do tvaru

(2)

Pro geometrickou představu dále sledujme schéma na obr. Enzymová kinetika, 2. část 1. Červeně vyznačený graf funkce tvaru klesající exponenciály má zřejmě největší sklon na svém levém konci. Tam zároveň nabývá svého maxima, tzn. i suprema. Infimum klesající exponenciální funkce je rovno nule, tedy výraz v čitateli zlomku v Enzymová kinetika, 2. část (2) nalézáme jako vyznačenou svislou vzdálenost. V bodě největšího sklonu sestrojíme tečnu ke grafu funkce Ta svírá s kladnou poloosou úhel jak je v obrázku vyznačeno. Z definice funkce tangens jakožto poměru délek protilehlé a přilehlé odvěsny v pravoúhlém trojúhelníku a ze zlomku v Enzymová kinetika, 2. část (2) identifikujeme time scale jakožto délku vodorovné odvěsny (vyznačeno modře).

Spočítáme time scale pro koncentraci komplexu při quasi-steady-state aproximaci. Z vyjádření Enzymová kinetika (27) vidíme, že roste z počáteční koncentrace k asymptotické koncentraci a její derivace zřejmě nabývá svého maxima pro Dosazením do Enzymová kinetika, 2. část (1) spočítáme, že time scale koncentrace komplexu je

(3)

Pokračujeme výpočtem time scale koncentrace substrátu při quasi-steady-state aproximaci. Ze záporného znaménka derivace Enzymová kinetika (35), z počátečních podmínek a asymptotického chování podle obr. Enzymová kinetika 6 je zřejmé, že koncentrace substrátu klesá z počáteční hodnoty na asymptoticky nulovou hodnotu, a že maximum derivace Enzymová kinetika (35) nastává v čase tedy pro Dosazením do Enzymová kinetika, 2. část (1) tak obdržíme time scale koncentrace substrátu

(4)

Druhou možností je použít Enzymová kinetika (25), tedy neaproximovanou diferenciální rovnici pro koncentraci substrátu. Rychlost poklesu koncentrace je i tomto případě největší pro a dostáváme tak jinou verzi time scale

(5)

V uvažovaném příkladu obdržíme po dosazení parametrů Enzymová kinetika (20) následující hodnoty time-scale:

(6)

Nyní se vrátíme k podmínce quasi-steady-state aproximace. Požadovali jsme, aby se koncentrace substrátu měnila mnohem pomaleji, než se mění koncentrace komplexu Jinak řečeno, čas potřebný pro významnou změnu má být mnohem delší, než čas potřebný pro významnou změnu Pomocí time scale obou koncentrací tedy tento požadavek matematicky vyjádříme podmínkou

(7)

V uvažované enzymové reakci dostáváme podíly time scale a tzn. koncentrace komplexu C se mění zhruba rychleji než koncentrace substrátu S. Lze ukázat, že vždy platí druhá podmínka v Enzymová kinetika, 2. část (7) je tedy silnější než podmínka první. Dosazením odvozených time scale Enzymová kinetika, 2. část (3), Enzymová kinetika, 2. část (4), Enzymová kinetika, 2. část (5) do Enzymová kinetika, 2. část (7) dostáváme podmínky pro platnost quasi-steady-state aproximace ve tvaru

(8)

Tyto podmínky jsou v praxi splněny např. pokud je počáteční koncentrace substrátu řádově větší než koncentrace enzymu, pokud jsou koncentrace enzymu a substrátu řádově menší než nebo pokud rychlostní konstanta tvorby produktu je dostatečně malá.