Logický neuron

Nejznámějším matematickým modelem neuronu je tzv. logický neuron nazývaný též McCullochův-Pittsův logický neuron. Americký neurofyziolog a kybernetik Warren Sturgis McCulloch (1898-1969) a Walter Harry Pitts Jr. (1923-1969), zabývající se matematickou logikou a početními neurovědami, tento model poprvé popsali roku 1943 v článku A logical calculus of the ideas immanent in nervous activity v odborném časopise Bulletin of Mathematical Biophysics.

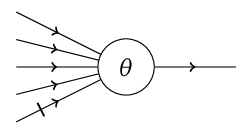
Obr. 1. Logický neuron s prahem se čtyřmi excitačními vstupy a jedním inhibičním vstupem.

McCullochův-Pittsův logický neuron bývá schematicky znázorňován tak, jak je ukázáno na obr. Matematické modely neuronu 1. Ve své nejjednodušší podobě můžeme takový neuron chápat jako zařízení s několika vstupy a jedním výstupem. Vstupy jsou kresleny jako spojnice s šipkami směřujícími do neuronu, výstup je reprezentován jednou spojnicí vycházející ze symbolu neuronu. Výstup se však může dělit a může být následně napojen do většího počtu (jiných) neuronů. Vstupy mohou být buď excitační, kreslené klasickou šipkou, anebo inhibiční, u nichž se ve schématu doplňuje kolmá čárka. Na výstupu se přitom objeví signál právě tehdy, když se současně signály objeví na určitém počtu vstupů. Tento minimální počet aktivních vstupů je nazýván práh a obvykle značen V nejjednodušším modelu může být práh rovný jakémukoliv nezápornému číslu.

Logický neuron je idealizací reálného neuronu a zachovává tak nejdůležitější charakteristické vlastnosti skutečného neuronu. Předpokládáme, že logický neuron může změnit svůj stav jen v diskrétních ekvidistantně vzdálených časových okamžicích. Výstup z jednoho neuronu se na vstupu napojených neuronů objeví v bezprostředně následujícím časovém kroku. Síť logických neuronů se chová synchronizovaně, okamžiky možné změny stavu jsou pro všechny neurony v síti totožné.

Biologové a neurofyziologové mohou tento model neuronu kritizovat pro přílišně až nereálné zjednodušení, zvlášť kvůli výše popsané časové závislosti. Na druhou stranu, obrovská výhoda logického neuronu je právě jeho jednoduchost. Ta často umožňuje analýzu očekávaného chování neuronové sítě, která by při zahrnutí jiných fyziologických parametrů neuronů byla příliš složitá. Logický neuron zachovává podstatné rysy chování reálného neuronu. Daní za jednoduchost modelu je zanedbání méně podstatných charakteristik reálného neuronu. Jedná se o obvyklý postup matematického modelování reálného světa. Často si musíme realitu zjednodušovat, abychom dokázali matematický model schůdně analyzovat a modelovat. Na provedená zjednodušení však přitom nezapomínáme, a jejich možný vliv na chování modelu diskutujeme.

Nyní podáme formální definici logického neuronu.

1. Logický neuron se může nacházet v jednom ze dvou stavů, které nazveme aktivní a neaktivní.

2. Logický neuron má jeden výstup, který může být současně napojen do jednoho nebo více jiných neuronů nebo také zpět do stejného neuronu. V každém okamžiku je na všech těchto napojeních stejný výstup.

3. Logický neuron má celkem vstupů, z nichž je excitačních a inhibičních. Počty excitačních i inhibičních vstupů mohou nabývat hodnot jakéhokoli nezáporných celých čísel.

4. Logický neuron má práh . V nejjednodušší podobě požadujeme obecně stačí

5. Čas je kvantizován, stav logického neuronu se může změnit pouze v diskrétních časových okamžicích (krocích), Stav logického neuronu zůstává nezměněn v časovém intervalu Délka časového kroku je stejná pro všechny neurony v síti, neuronová síť je synchronizovaná.

6. Daný vstup je aktivní v čase právě tehdy, když neuron, jehož výstupem uvažované spojení je, byl aktivní v čase Označujeme počet aktivních excitačních vstupů a počet aktivních inhibičních vstupů v čase Zřejmě platí v každém čase

7. Logický neuron je aktivní v čase tedy přesněji ve všech časech právě když

   (1)

   Konstanta charakterizuje požadovaný poměr mezi počtem aktivních excitačních a aktivních inhibičních vstupů pro dosažení aktivního výstupu neuronu. Často je resp. v nejjednodušším případě

Logický neuron je binárním zařízením, protože se vždy nachází právě v jednom ze dvou možných stavů, aktivním, anebo neaktivním. V matematické či logické notaci často označujeme aktivní stav hodnotou 1 a neaktivní stav hodnotou 0. Máme-li síť neuronů označených čísly od 1 do m, můžeme stav všech neuronů v této síti v každém čase jednoznačně reprezentovat binárním číslem délky kdy stav -tého neuronu je kódován číslicí na -tém místě binárního zápisu. Počet všech možných stavů celé sítě je rovný

Nyní si uvedeme několik příkladů logických neuronů a jednoduchých neuronových sítí, na kterých ukážeme, že i takto jednoduchý model neuronu stačí k vytvoření primitivního mozku nebo oscilujícího systému. Zdůrazněme hned na počátku, že se jedná jen o velmi jednoduché ukázky pro pochopení funkce logických neuronů. V reálném mozku je totiž řádově neuronů, každý s nejméně vstupy.

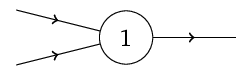
Obr. 2. Logický neuron s prahem 1 a dvěma excitačními vstupy.

Na obr. Matematické modely neuronu 2 je neuron s excitačními a inhibičními vstupy a prahovou hodnotou . Tento neuron je dle vii aktivní, pokud tj. pokud je aktivní alespoň jeden z jeho (excitačních) vstupů. Pokud by tento neuron měl prahovou hodnotu může být aktivní, přestože by nebyl aktivní žádný z jeho vstupů. Takový neuron je někdy nazýván spontánně aktivní.

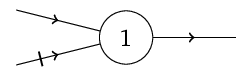
Obr. 3. Logický neuron s prahem 1, jedním excitačním vstupem a jedním inhibičním vstupem.

Na obr. Matematické modely neuronu 3 vidíme neuron s excitačním a inhibičním vstupem a prahovou hodnotou Předpokládejme a vypišme si možné případy aktivních a neaktivních vstupů spolu s hodnotou Výsledek je v Matematické modely neuronu tab. 1. Podmínka vii je splněna pouze v případě neuron je tedy aktivní pouze tehdy, když je excitační vstup aktivní a inhibiční vstup neaktivní. Pokud by neuron měl práh byl by spontánně aktivní, ale bylo by možné jej udržet v neaktivním stavu při aktivním inhibičním a neaktivním excitačním vstupu.

Tab. 1. Funkce logického neuronu z obr. Matematické modely neuronu 3 pro = 1.

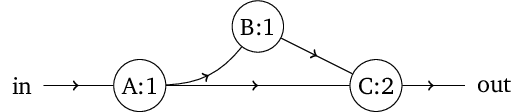
Obr. 4. Primitivní mozek ze sítě 3 logických neuronů, reagující (out) na bezprostředně opakovanou aktivitu na vstupu (in).

Schéma na obr. Matematické modely neuronu 4 představuje síť 3 neuronů s pouze excitačními vstupy, jedním externím vstupem (in) a výstupem (out). Chování této sítě v závislosti na časovou posloupnost aktivity vstupu uvádí Matematické modely neuronu tab. 2. Je zřejmé, že výstup je aktivní pouze tehdy, když v předchozích (alespoň) dvou po sobě jdoucích krocích byl vstup aktivní. Tato jednoduchá neuronová síť tak může představovat velice primitivní mozek, jehož funkcí je reagovat na bezprostředně opakovanou aktivitu na vstupu.

Tab. 2. Odpověď primitivního mozku (out) ze sítě tří logických neuronů podle obr. Matematické modely neuronu 4 pro = 1 jako reakce na časovou řadu (in), k značí pořadí kroků. Tento primitivní mozek dokáže rozeznat (aktivní out) aktivní vstup (in) ve dvou po sobě jdoucích časových krocích.

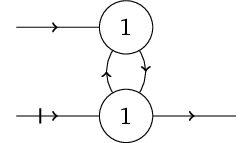
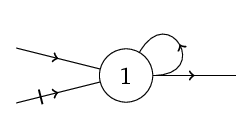
Obr. 5. Self-re-excitující systémy jako modely primitivní paměti.

Na obr. Matematické modely neuronu 5 jsou dva příklady tzv. self-re-excitujících neuronových sítí. Aktivní excitační vstup v jediném čase způsobí, že výstup těchto systémů se stane aktivním a zůstane aktivním i bez dalších aktivních vstupů. Výstup lze pak deaktivovat jedině aktivováním inhibičního vstupu, přičemž výstup zůstane neaktivní opět až do aktivování excitačního vstupu. Výstup tedy může mýt měněn na dlouhou dobu pomocí aktivního vstupu v jediném čase. Takové systémy mohou představovat primitivní paměť.

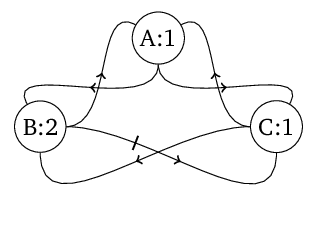
Obr. 6. Síť logických neuronů tvořící oscilující systém.

Tři logické neurony spojené podle schématu na obr. Matematické modely neuronu 6 tvoří izolovanou síť. Neurony A a C mají prahovou hodnotu rovnu 1, neuron B má prahovou hodnotu rovnou 2. Vstup z B do C je inhibiční, ostatní vstupy jsou excitační a předpokládáme Jaký bude vývoj aktivity této sítě, když ji začneme pozorovat v některém z možných stavů? Využijeme zápisu pomocí binárního zápisu. Ciferný zápis čísla ve dvojkové soustavě kóduje po řadě stav neuronu A, B, a C. Např. 101 značí stav, kdy neurony A a C jsou aktivní, neuron B je neaktivní. 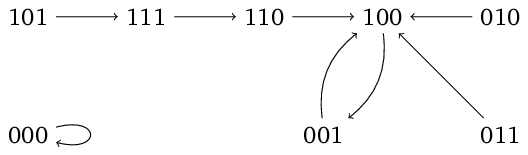Uvedená síť se může nacházet v kterémkoliv z možných stavů. Přechodový diagram (ověření přenecháváme čtenáři jako cvičení)

(2)

popisuje vývoj aktivity sítě v čase, každá šipka znázorňuje změnu stavu za krok délky Vidíme, že pokud síť začne pracovat v kterémkoliv stavu jiném než 000 (všechny neurony neaktivní), po několika krocích dospěje k oscilačnímu chování, kdy se pravidelně budou měnit stavy 001 a 100, tedy aktivní bude střídavě vždy pouze neuron A a C, neuron B bude neaktivní.