Základní princip enzymové reakce

Historie matematického popisu modelů enzymové kinetiky je spojena především se jmény  Leonora Michaelise (1875-1949), německého biochemika, fyzikální chemika a fyzika, a Maud Mentenové (1879-1960), kanadské lékařky, působící od roku 1912 v Berlíně.

Enzymy umožňují přeměnu molekul jedné látky na molekuly látky jiné. Vstupní látka, která se má transformovat, se nazývá substrát a látka, která reakcí vzniká, se nazývá produkt, budeme pro ně proto užívat zkratky S a P. V typických reakcích enzymy (zkratka E) urychlují (katalyzují) proces přeměny látek tím, že se na sebe váží substrát za vzniku tzv. komplexu enzym-substrát (označení C, někdy též ES). Tento komplex C se pak může za určitých podmínek rozpadnout na volný enzym E a produkt P. Tato přeměna však může také selhat v tom smyslu že komplex C se rozpadne zpět na volný enzym E a substrát S. Předpokládáme tedy, že vázání enzymu na substrát je reverzibilní, zatímco příp. rozpad komplexu na E a P je ireverzibilní. Kinetické schéma této enzymové reakce je

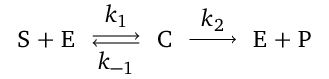(14)

Rychlostní konstanty a jsou pak po řadě spojeny se vznikem komplexu (syntéza),  rozpadem komplexu na substrát (analýza) a s formováním produktu z komplexu (analýza).  Konstanta je, stejně jako konstanta spojena s analýzou komplexu C, má tedy i stejnou jednotku, s^-1.

Použitím principu law of mass action lze pak pro koncentrace jednotlivých látek, tedy komplexu enzym-substrát, volného enzymu, substrátu, a produktu jakožto funkci času psát čtyři diferenciální rovnice

	(15)
	(16)
	(17)
	(18)

spolu s počátečními podmínkami

(19)

Na začátku reakce je množství produktu nulové, v praxi je často nulová i počáteční koncentrace komplexu

Při známých konstantách a hodnotách počátečních koncentrací lze vývoj koncentrací určit numericky. Pro numerické výpočty a grafická zobrazení budeme v celé této kapitole uvažovat následující hodnoty parametrů:

(20)

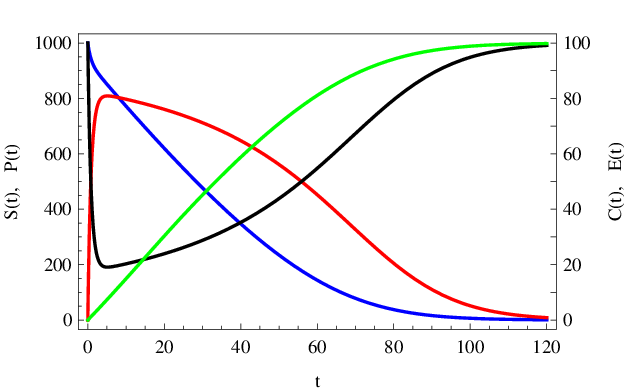
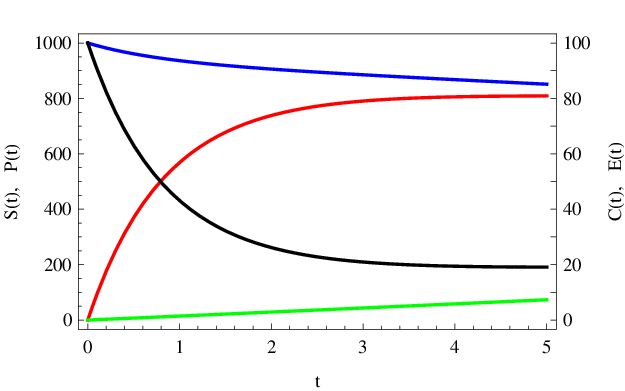
Numericky získaná řešení počáteční úlohy Enzymová kinetika (15) - (19) s těmito parametry jsou vykreslena v obr. Enzymová kinetika 1 a Enzymová kinetika 2.

Obr. 1. Numericky spočítané průběhy (čas v sekundách) koncentrací (mol dm-3) substrátu S(t) (modře), produktu P(t) (zeleně), volného enzymu E(t) (černě) a komplexu enzym-substrát C(t) (červeně) podle kinetického schématu Enzymová kinetika (14) s parametry Enzymová kinetika (20). Koncentrace C(t) a E(t) mají odlišné škálování podle měřítka na pravé straně grafu.

Obr. 2. Detail z obr. Enzymová kinetika 1 zobrazující koncentrace v počáteční fázi reakce.

Vidíme, že koncentrace substrátu s rostoucím časem klesá, a to přibližně exponenciálně, a koncentrace produktu roste. Koncentrace volného enzymu nejdříve klesá, poté se zvolna vrací k počáteční koncentraci Koncentrace komplexu naopak nejdříve roste a poté zvolna klesá k nule. Pro dojde ke stabilizaci systému, všechen substrát bude postupně přeměněn na produkt a enzym po ukončení této reakce zůstane opět výhradně ve volné formě.

Pro analýzu úlohy Enzymová kinetika (15)-(19) bychom kromě numerických výsledků potřebovali i přesná řešení v analytickém tvaru. Jejich výpočet je však i pro uvažovanou reakci velmi složitý, běžnými postupy systém vyřešit neumíme, systém diferenciálních rovnic totiž není lineární.

Ukážeme proto tzv. quasi-steady-state aproximaci, která poskytuje jednoduchý a užitečný, ale přitom relativně přesný, pohled na interakci enzym-substrát-produkt. Kromě odvození přibližného řešení systému diferenciálních rovnic ukážeme i obecný postup, jak složitý systém zjednodušit na aproximovaný systém a jak zároveň zhodnotit přesnost aproximace a ověřit podmínky pro její platnost.

Než se budeme aproximaci věnovat, všimněme si ještě některých závislostí v úloze Enzymová kinetika (15)-(19). Koncentrace produktu vystupuje pouze v rovnici Enzymová kinetika (18) a k jejímu výpočtu potřebujeme znát průběh koncentrace komplexu. Nejdříve je tedy nutné vyřešit systém první tří diferenciálních rovnic pro koncentrace koncentraci produktu pak nalezneme integrováním koncentrace komplexu,

(21)

Sečtením rovnic Enzymová kinetika (15) a Enzymová kinetika (16) dostaneme

(22)

tzn. součet koncentrací a je konstantní, podle Enzymová kinetika (19) rovný

(23)

Enzym se tedy v reakci vlastně vyskytuje ve dvou formách: jako volný E a jako vázaný v komplexu C. To je patrné i na časových průbězích koncentrací a v obr. Enzymová kinetika 1 a Enzymová kinetika 2. Z Enzymová kinetika (23) vyjádříme koncentraci a dosadíme do rovnic Enzymová kinetika (15) a Enzymová kinetika (17). Tím nám v systému zůstanou pouze dvě diferenciální rovnice

	(24)
	(25)

pro koncentrace a s počátečními podmínkami

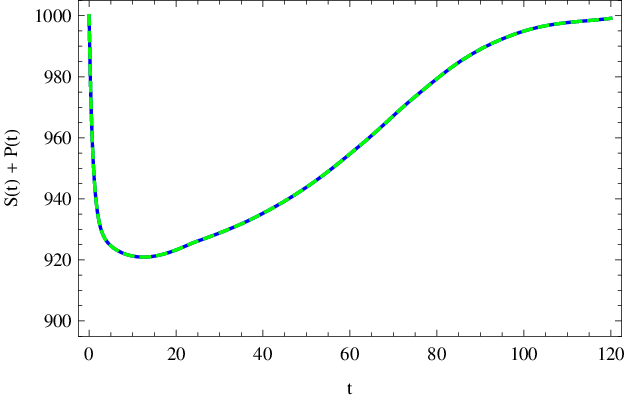
Součet koncentrací substrátu a produktu však obecně konstantní není. Všechen substrát se sice přemění na produkt, ale součet jejich koncentrací je roven pouze na začátku a na konci reakce, jak je patrné z následujícího obrázku.

Obr. 3. Součet koncentrací ( mol dm-3) S(t) + P(t) substrátu a produktu v čase (sekundy) podle kinetického schématu Enzymová kinetika (14) s parametry Enzymová kinetika (20).