
Úlohy k procvičení
Cvičení 1. Mějme alternativní rozložení s pravděpodobnostní funkcí a
kde
Určete Shannonovu entropii jako funkci parametru
Řešení
Dosazením do Vybraná témata z teorie informace (2) dostáváme
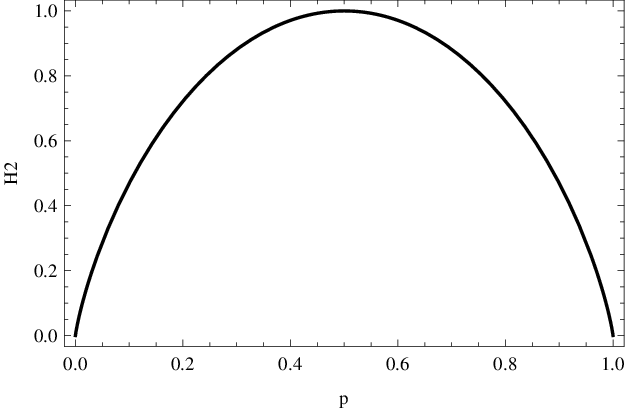
Entropie alternativního rozdělení se v teorii informace vyskytuje poměrně často, proto se užívá speciálního označení Funkce
je vykreslena na následujícím obrázku. Maximální entropie, 1 bit, odpovídá hodnotě p=0,5, tedy maximálně náhodnému alternativnímu rozdělení. Naopak, pro hodnoty p=0 a p=1 je výsledek pozorování
deterministický (nenáhodný), a tedy entropie je nulová.
 |
|
Obr. 1. Entropie binárního rozdělení s parametrem p.
|
Cvičení 2. Mějme náhodnou veličinu s Gaussovým (normálním) rozdělením s nulovou střední hodnotou a rozptylem
tzn. s hustotou
Určete diferenciální entropii náhodné veličiny
jakožto funkci směrodatné odchylky
Řešení
Přímou aplikací Vybraná témata z teorie informace (27) dostáváme
|
|
|
|
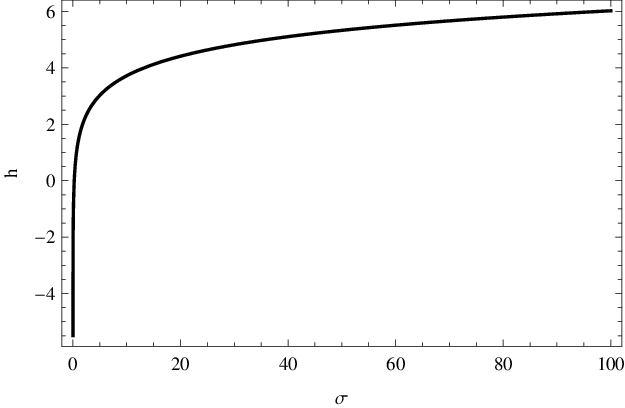
Výsledek je jako funkce směrodatné odchylky
vykreslen na obr. 2.
 |
|
Obr. 2. Diferenciální entropie Gaussova rozdělení s rozptylem
|
Cvičení 3. Střelec střílí do dvou terčů, do velkého terče dvakrát a do malého terče třikrát. Pravděpodobnosti zásahu v každém pokusu jsou rovny při střelbě do velkého a
při střelbě do malého terče. Do kterého z terčů je výsledek střelby, daný počtem zásahů, méně neurčitý? Který terč má menší směrodatnou odchylku počtu zásahů? Spočítejte i střední hodnoty obou veličin.
Řešení
Označme náhodnou veličinou počet zásahů do malého a
počet zásahů do velkého terče. Uvedené náhodné veličiny se řídí binomickým rozdělením pravděpodobnosti,
a jejich pravděpodobnostní funkce jsou rovny
Dosazením do Vybraná témata z teorie informace (2) dostáváme
výsledek střelby do malého terče je tedy méně neurčitý. Dále spočítáme směrodatné odchylky obou náhodných veličin,
výsledek střelby do malého terče má i menší směrodatnou odchylku. Střední hodnoty obou veličin jsou si rovny,
Cvičení 4. Pokračujme v příkladu Cvičení 3 se střelbou do dvou terčů. Za každý zásah do malého terče se vyplácí odměna 100 Kč, za každý zásah do velkého terče pak 50 Kč. Náhodná veličina udává celkovou výhru střelce na malém terči, náhodná veličina
pak celkovou výhru na velkém terči. Spočítejte střední hodnoty obou náhodných veličin. Která z veličin
je méně neurčitá? Která z veličin
má menší směrodatnou odchylku?
Řešení
Náhodné veličiny udávající výhry na terčích již nemají binomické rozdělení. Jejich rozdělení pravděpodobnosti je stejné, ale na jiných realizacích,
Obdržíme opět stejné střední hodnoty výher,
Dále počítáme druhé momenty obou náhodných veličin a následně určíme směrodatné odchylky,
Vidíme, že směrodatná odchylka je nižší u výhry na malém terči. Jak dopadnou výpočty entropie? Výsledky budou zcela stejné jako v příkladu Cvičení 3, neboť v Vybraná témata z teorie informace (2) nikde nevystupují hodnoty realizací náhodných veličin,
Výše výhry na malém terči je tedy méně neurčitá (méně náhodná), ale má větší směrodatnou odchylku. Entropie a směrodatná odchylka (resp. rozptyl) tedy nepopisují stejné vlastnosti náhodných veličin. Směrodatná odchylka (rozptyl) kvantifikuje průměrné vychýlení výsledku náhodného pokusu od střední hodnoty, zatímco entropie popisuje neurčitost (náhodnost) výsledku a nebere do úvahy jeho hodnotu.
Cvičení 5. Spočítejte entropii diskrétního rovnoměrného rozdělení pravděpodobnosti na množině
Řešení
Dosazením do Vybraná témata z teorie informace (2) dostáváme
Tento výsledek odpovídá situaci, kdy potřebujeme předat informaci o tom, který z možných výsledků nastal, a to co nejúsporněji, tzn. např. co nejkratším binárním kódem. Pokud by některý z výsledků měl velkou pravděpodobnost, přiřadili bychom mu krátký kód, zatímco málo pravděpodobným výsledkům bychom přiřadili delší kódový zápis. V našem případě jsou však všechny výsledky stejně pravděpodobné a stačí tedy přenést binárně zapsanou informaci o pořadí toho výsledku, který nastal. K tomu budeme ve dvojkové soustavě potřebovat právě nejméně
bitů.
Cvičení 6. Spočítejte diferenciální entropii exponenciálního rozdělení pravděpodobnosti jako funkci intenzity
Řešení
|
|
|
|
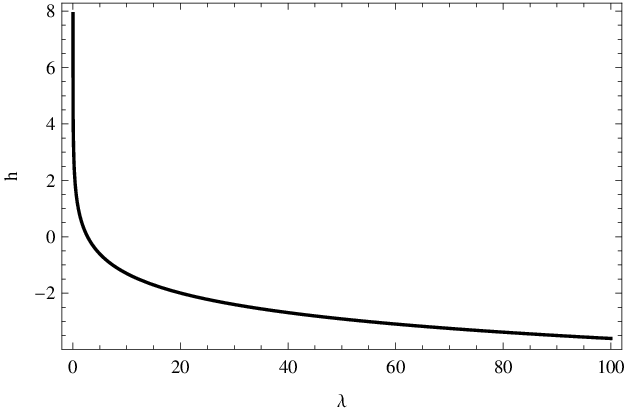
Graf je na vykreslen na obr. Vybraná témata z teorie informace 3.
 |
|
Obr. 3. Diferenciální entropie exponenciálního rozdělení s intenzitou
|
Cvičení 7. Spočítejte diferenciální entropii rovnoměrného spojitého rozdělení pravděpodobnosti na intervalu
Řešení
Dosazením hustoty
do Vybraná témata z teorie informace (27) dostáváme
Entropie rovnoměrného spojitého rozložení logaritmicky závisí na délce intervalu hodnot náhodné veličiny.




