
Z-transformace, přenosová funkce diskrétního systému
Transformace Z je důležitým matematickým nástrojem pro reprezentaci a manipulaci s diskrétními posloupnostmi[1]. Můžeme ji považovat za zevšeobecnění Fourierovy transformace pro diskrétní systémy a signály.
Obraz diskrétní posloupnosti v Z-transformaci je dán mocninnou řadou:
|
|
(3.1)
|
přičemž nejčastěji uvažujeme tzv. jednostrannou Z-transformaci pro nezáporné indexy . Jak ukazuje rovnice (2.7), není samoúčelné se Z-transformací zabývat, neboť obraz konvoluce vykazuje zajímavé vlastnosti:
|
|
(3.2)
|
Z rovnice (3.2) vyplývá, že násobení obrazů v Z-transformaci odpovídá konvoluce původních posloupností v časové nebo prostorové doméně. Tato vlastnost Z-transformace se označuje jako konvoluční teorém[2] a obraz impulsní charakteristiky diskrétního systému se označuje jako přenosová funkce diskrétního systému:
|
|
(3.3)
|
Z rovnice (3.1) vyplývá, že přenosová funkce vyjadřuje na jednotkové kružnici frekvenční charakteristiku diskrétního systému, což může lépe osvětlit periodicitu frekvenční charakteristiky, a to zejména při srovnání obrázku 3.1 a obrázku 3.2.
Pokud se vyjádří přenosová funkce ve tvaru racionálně lomené funkce a provedou se úpravy obou polynomů v čitateli a ve jmenovateli tak, aby se jednalo o polynomy s kladnými mocninami z, je pak možné vyjádřit čitatel a jmenovatel přenosové funkce pomocí součinu kořenových činitelů:
|
|
(3.4)
|
Kořeny polynomu v čitateli se označují jako nulové body přenosové funkce a kořeny polynomu ve jmenovateli se označují jako póly přenosové funkce.
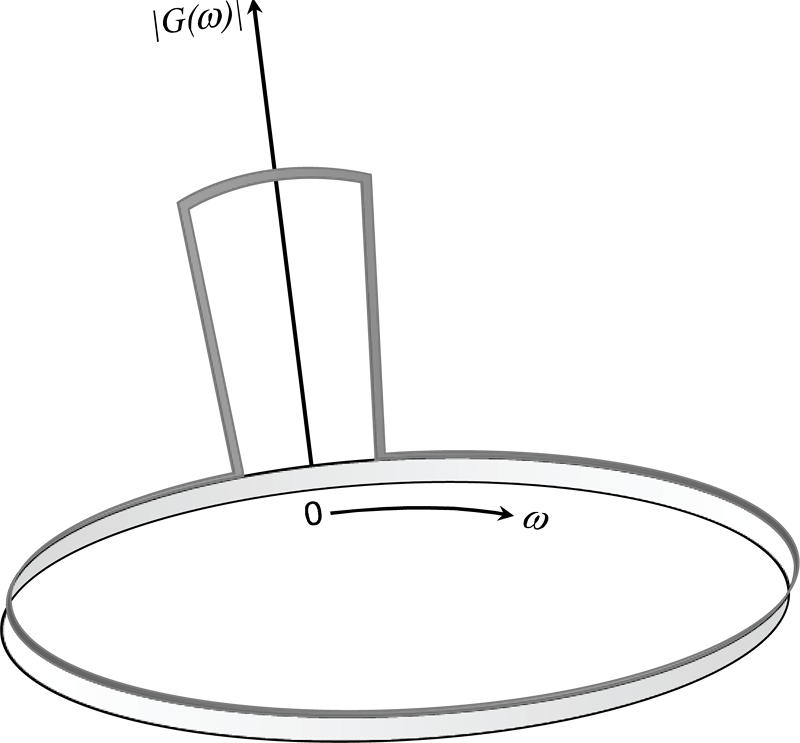
Obr. 3.1: Přenosová funkce na jednotkové kružnici |z|=1 vyjadřuje frekvenční charakteristiku systému – zde se jedná o idealizovanou dolní propust z obrázku 2.3.
Rozložení nul a pólů v rovině z je dalším typem popisu diskrétního systému. Využívá se zejména v situacích, kdy je cílem u systému nebo jeho modelu vyšetřit jeho stabilitu[3]. Jedno ze dvou kritérií stability stanovuje, že diskrétní systém je stabilní, pokud jsou všechny póly jeho přenosové funkce umístěny uvnitř jednotkové kružnice. Toto kritérium se označuje také jako kritérium stability v obrazové doméně. Druhé kritérium stability diskrétního systému je definováno v časové doméně. Podle něj je systém stabilní, pokud součet absolutních hodnot vzorků jeho impulsní charakteristiky je konečné číslo.
Přímou souvislost konfigurace nulových bodů a pólů přenosové funkce systému s frekvenční charakteristikou systému ukazují následující rovnice a obrázek 3.2.
|
|
|
|
|
(3.5)
|
|
|
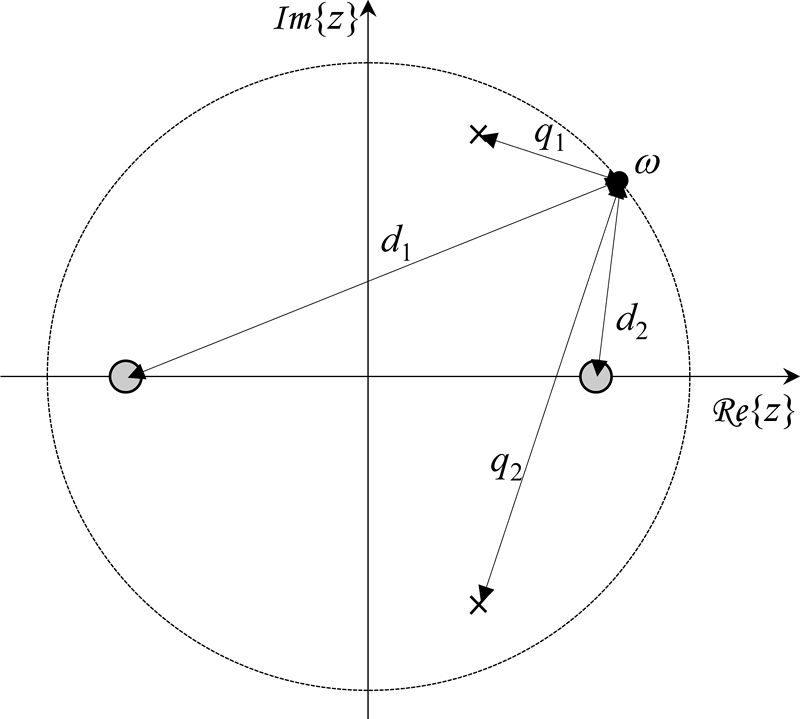
Obr. 3.2: Rozložení nulových bodů
a pólů
přenosové funkce systému v rovině z může být využito pro sestavení odhadu průběhu frekvenční charakteristiky, viz rovnice (3.5).
Průběh modulové frekvenční charakteristiky lze z konfigurace nulových bodů a pólů přenosové funkce odhadnout tak, že se pro každou úhlovou frekvenci , které odpovídá bod na jednotkové kružnici
, určí vzdálenosti tohoto bodu od všech nulových bodů
a dále vzdálenosti tohoto bodu od všech pólů
. Podíl součinů těchto vzdáleností, viz rovnice (3.5), pak určuje hodnotu modulové frekvenční charakteristiky pro danou úhlovou frekvenci
. Obdobně se postupuje také u odhadu průběhu fázové frekvenční charakteristiky, přičemž se zde pracuje nikoli se vzdálenostmi, ale s úhly, které svírají průvodce vyšetřovaných bodů s reálnou osou.
V úvodu bylo uvedeno, že jedním ze základních způsobů popisu diskrétního systému je diferenční rovnice. Souvislost diferenční rovnice s popisem systému pomocí přenosové funkce sice není na první pohled zřejmá, ale pokud roznásobíme zlomky v rovnici (3.4):
|
|
(3.6)
|
koeficienty a
se normalizují tak, aby
, a aplikuje se inverzní z-transformace včetně vět o linearitě a posunu (zde bez důkazu, podrobně viz např. [1]), získá se diferenční rovnice systému:
[1] Z-transformace nemá nic společného s tzv. z-score transformací, která se aplikuje ve statistické matematice pro převod libovolné normální distribuce na standardní normální distribuci.
[2] Konvoluční teorém platí také pro speciální případy Z transformace, a sice pro DTFT a DFT.
[3] Stabilitu systému je možno vysvětlit jako jeho tendenci přiměřeně reagovat na trvající podnět a vracet se do výchozího stavu po té, co podnět zanikne.




