Systémy, signály a časové řady

Za systém se obvykle považuje soustava entit a jejich vzájemné vztahy. V reálném světě jsou systémy příliš složité, a ty živé obzvlášť, na to, aby je bylo možné jednoznačně popsat nebo analyzovat v celé jejich komplexnosti. Využívají se proto často matematické modely, které vznikají abstrakcí reálných systémů. Model by měl být jednoduchý a měl by vykazovat takové chování, jaké je pozorováno u systému, jenž je předmětem zájmu. Abstrakcí je myšleno vymezení důležitých veličin reálného systému a jejich vzájemných vztahů, přičemž ostatní veličiny tvoří okolí systému a mohou být ignorovány, či mohou ovlivňovat vstupy systému nebo mohou být ovlivňovány jeho výstupy.

Systém mnohdy vysílá spontánně či vynuceně různé signály a mění svoje stavy – mňouká, štěká, přibírá na váze, stárne, umírá, nebo v případě populace třeba i vymírá či se nestabilně množí. Pokud pozorovatel tyto signály a stavy měří, tj. neznámý systém pozoruje, pak vlastně získává o neznámém systému experimentální data, viz obrázek 1.1.

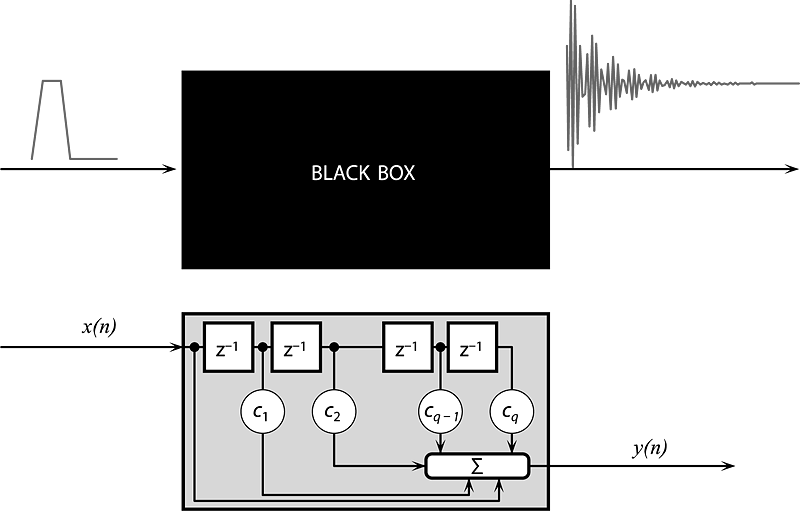
Obr. 1.1: Identifikace systémů je disciplína zabývající se tvorbou matematických modelů systémů. Identifikace začíná pozorováním či měřením modelovaného systému – jsou tak získána experimentální data, která se pak využívají pro identifikaci struktury a pro odhad parametrů modelu. Data mohou být mj. reprezentována časovými řadami neboli 1-D diskrétními signály. Systémy nebo procesy mohou signály vysílat jednak spontánně nebo jako odezvu na buzení vstupním signálem. Popisem systému se vysvětlují souvislosti mezi signály či časovými řadami na výstupu a na vstupu. Na ilustračním schématu je znázorněn diskrétní systém, který je realizován pomocí zpožďovacích členů z^-1, dále pomocí operací násobení koeficienty c_1..q a také pomocí operace sčítání. Systém zpracovává vstupní časovou řadu x(n) a na výstup vrací časovou řadu y(n).

Identifikací systému se rozumí sestavení modelu reálného systému a odhadnutí jeho parametrů tak, aby chování modelu odpovídalo tomu, co je v reálném světě pozorováno. Častou aplikací je konstrukce modelu za účelem předpovědi budoucího chování systému, který je modelován. Systémy nebo jejich modely se často popisují soustavami diferenciálních nebo diferenčních rovnic. V teorii systémů a signálů se velmi často používají také neparametrické způsoby popisu, a to prostřednictvím charakteristik v originální časové či prostorové doméně, nebo po vhodných transformacích ve frekvenční doméně. Z hlediska zpracování a analýzy časových řad je možno definovat systém jako jakoukoli sadu procesů, které náhodně nebo systematicky ovlivňují povahu časové řady, viz příklad na obrázku 1.2.

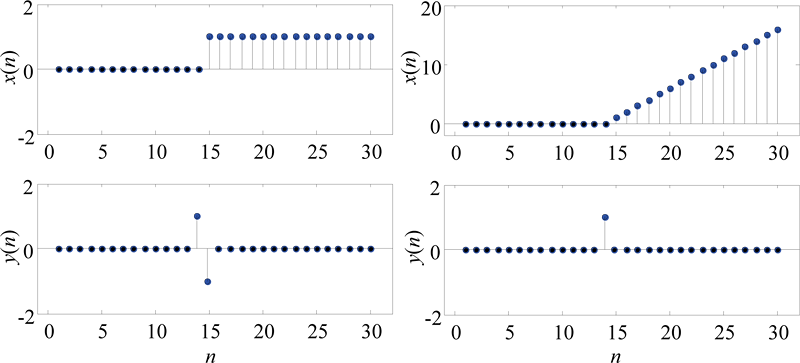
Obr. 1.2: Příklad systému pracujícího s diskrétními 1-D signály neboli časovými řadami. Vstupní časové řady x(n) jsou zpracovány hranovým detektorem tak, že lze výstupní časové řady y(n) použít pro detekci bodu zlomu v původních časových řadách. Hranový detektor lze popsat následující diferenční rovnicí: y(n)=x(n+1)-2x(n)+x(n-1). Jedná se tedy o nekauzální systém.

Pro pojem signál existuje v literatuře celá řada definic. Pro účely tohoto výukového materiálu textu bude podle [1] signál definován jako jev fyzikální, chemické, biologické, ekonomické či jiné materiální povahy, který nese nehmotnou informaci o stavu a dynamice systému či procesu, který jej generuje. Je-li zdrojem informace živý organismus, pak hovoříme o biosignálech, a to bez ohledu na podstatu nosiče informace. Z pohledu matematika je možno se dívat na signál jako na funkci v čase nebo v prostoru proměnných a měřitelných veličin.

Signály se dělí podle nezávislých veličin na spojité nebo diskrétní, viz obrázek 1.3. Příkladem přirozeně spojitých veličin může být elektrické napětí, teplota, tlak, koncentrace chemických látek apod. Příkladů přirozeně diskrétních signálů najdeme v reálném světě sice méně, ale určitě existují, a to např. četnosti populace n-té generace, sekvence bází v DNA apod. Signály se rozlišují také podle počtu dimenzí nezávislých veličin na jednorozměrné 1‑D, dvourozměrné 2‑D, třírozměrné 3‑D, čtyřrozměrné 4‑D a vícerozměrné N‑D. U vícerozměrných signálů jde většinou o statické nebo dynamické obrazy definované pomocí dvou až čtyř časoprostorových souřadnic, zatímco jednorozměrné signály zpravidla reprezentují časové průběhy veličin. V případě jednorozměrných diskrétních signálů s ekvidistantním vzorkováním se pak hovoří o časových řadách.

Obr. 1.3: Jednorozměrný spojitý signál (vlevo) a jednorozměrný diskrétní signál neboli časová řada (vpravo). Zatímco spojitý signál je funkcí času t, časová řadou rozumíme posloupnost vzorků s bezrozměrným indexem n. Někdy může být fyzikální význam nezávislé veličiny časové řady zdůrazněn zápisem x(nT), kde T je vzorkovací perioda, což je časový interval mezi dvěma sousedními vzorky.

Při řešení úloh spojených s analýzou časových řad, je potřeba mít na paměti fakt, že hodnoty vzorků časové řady jsou výsledkem analogově-digitálního převodu (A/D převodu) spojitého signálu. Tento převod v sobě zahrnuje dvě operace: 1) diskretizaci podél časové či prostorové osy, tj. vzorkování, a 2) diskretizaci podél osy závislé veličiny, tj. kvantování neboli zaokrouhlování odečtených hodnot na kvantizační hladiny. Obě operace jsou naznačeny na obrázku 1.4 a dále jsou rozebrány důsledky nevhodně nastavených parametrů těchto obou operací.

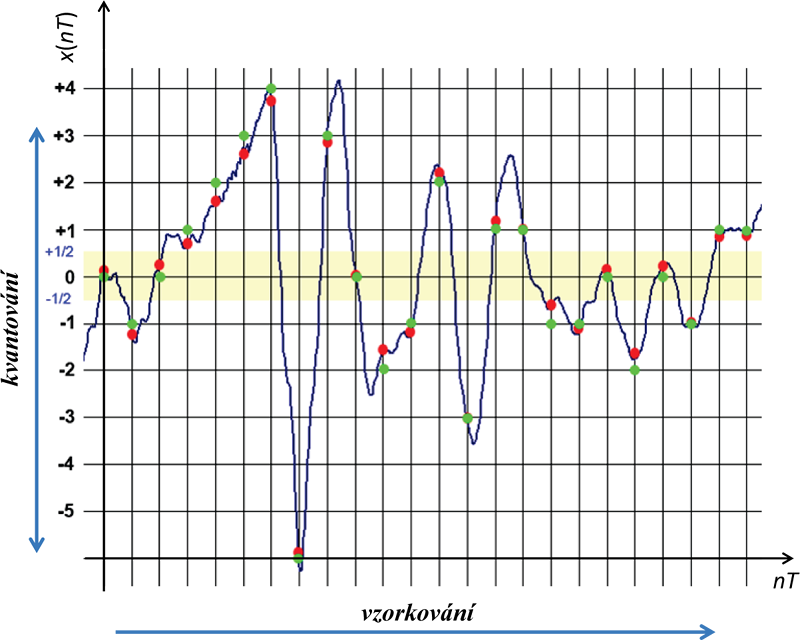
Obr. 1.4: Analogově-digitální převod spojitého signálu x(t) na signál diskrétní x(nT) zahrnuje dvě operace: vzorkování s periodou T a kvantování. Výstupem A/D převodu je posloupnost hodnot, které jsou jednak výsledkem odečítání v diskrétních okamžicích časové osy (červené puntíky) a dále zaokrouhlení na kvantizační hladiny (zelené puntíky). Rozpětí kvantizačních hladin (žlutý pruh) vyznačuje maximální chybu kvantování. Tato chyba způsobuje tzv. kvantizační šum.

Pokud spojitý signál neobsahuje složky s frekvencí nad , pak je veškerá informace nesená signálem obsažena v posloupnosti jeho vzorků , a to jen v případě, je-li při vzorkování splněna podmínka^[1]:

kde je vzorkovací frekvence, což je převrácená hodnota vzorkovací periody . Je-li splněna tato podmínka (1.1), lze z posloupnosti vzorků signálu dokonale rekonstruovat původní analogový signál . Pokud tato podmínka splněná není, dochází při A/D převodu ke zkreslení, které se označuje jako aliasing, viz obrázek 1.5.

Obr. 1.5: Ukázka zkreslení vzniklého nevhodně provedeným podvzorkováním dvourozměrného signálu (obrazu). Původní obraz obsahoval strukturu (cihly domu), jejíž střídání je ve scéně rychlejší, než byla zvolena vzorkovací frekvence obrazu. Zkreslení (aliasing), které je způsobené prolínáním dvou rastrů (jednoho skutečného a jednoho vzorkovacího), se v obrazu projevuje tzv. moaré efektem.

Kvantizační šum vzniká zaokrouhlováním na kvantizační hladiny. Jeho úroveň přímo souvisí s počtem těchto hladin. A/D převodník je zpravidla zařízení fungující ve dvojkové soustavě, a má tudíž počet kvantizačních hladin uvedený vždy pomocí počtu bitů N tak, že počet kvantizačních hladin je číslo 2^N. Je možno setkat se také s jiným způsobem popisu kvality A/D převodu, a to pomocí poměru signálu a kvantizačního šumu (signal-to-noise ratio):

kde  označuje výkon signálu, který je úměrný druhé mocnině jeho amplitudy. Tento poměr v rovnici (1.2), vyjádřený bezrozměrně nebo i v decibelech, lze evidentně přímo vyjádřit i jako funkci počtu bitů A/D převodníku N, jak je ukázáno v řešené úloze 1.